Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
8. Элементы теории конечного поля. Линейные рекуррентные последовательности над конечными полями. Результаты, полученные в теории линейных рекуррентных последовательностей над конечными полями, находят в настоящее время практическое применение для генерации последовательностей псевдослучайных чисел с гарантированно хорошими для криптографии свойствами и служат основой для построения современных поточных криптосистем. Поэтому рассмотрим принципы построения линейных рекуррентных последовательностей и важнейшие теоретические результаты, связанные с ними и полученные в рамках теории конечных полей. Определение. Пусть к - натуральное число, 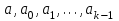 - заданные элементы конечного поля - заданные элементы конечного поля  . Последовательность . Последовательность 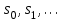 элементов поля элементов поля  , удовлетворяющая соотношению , удовлетворяющая соотношению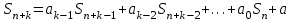 , , 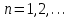 называется линейной рекуррентной последовательностью (ЛРП) K - го порядка над полем называется линейной рекуррентной последовательностью (ЛРП) K - го порядка над полем  . .Первые члены 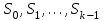 однозначно определяют всю последовательность и называются начальными значениями. Такое соотношение еще называют линейным рекуррентным соотношением K - го порядка. Будем считать, что линейное рекуррентное соотношение K - го порядка (К - го порядка над полем однозначно определяют всю последовательность и называются начальными значениями. Такое соотношение еще называют линейным рекуррентным соотношением K - го порядка. Будем считать, что линейное рекуррентное соотношение K - го порядка (К - го порядка над полем  ) называется однородным, если q=0, в противном случае - неоднородным. ) называется однородным, если q=0, в противном случае - неоднородным.Пример. Пусть порядок К=4, тогда имеем линейную рекуррентную последовательность 4 порядка над полем  вида: вида: 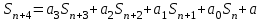 . .В практическом плане линейные рекуррентные последовательности реализуются на базе современных компьютерных систем, работающих на основе двузначной логики. Все числовые данные в ЭВМ представляются с помощью элементов двух типов 0 и 1. Т.е. вся обработка информации осуществляется на основе элементов простого конечного поля 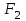 или его расширений или его расширений 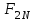 . Реализация линейных рекуррентных последовательностей над полем . Реализация линейных рекуррентных последовательностей над полем 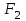 может быть достаточно просто осуществлена на основе регистров сдвига с обратной связью. Пусть у нас имеется однородное линейное рекуррентное соотношение вида (т.е. порядка К=4): может быть достаточно просто осуществлена на основе регистров сдвига с обратной связью. Пусть у нас имеется однородное линейное рекуррентное соотношение вида (т.е. порядка К=4): 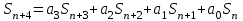 , , 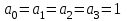 . Тогда его реализация на основе регистра сдвига из К=4 разрядов с обратной связью будет иметь вид: . Тогда его реализация на основе регистра сдвига из К=4 разрядов с обратной связью будет иметь вид: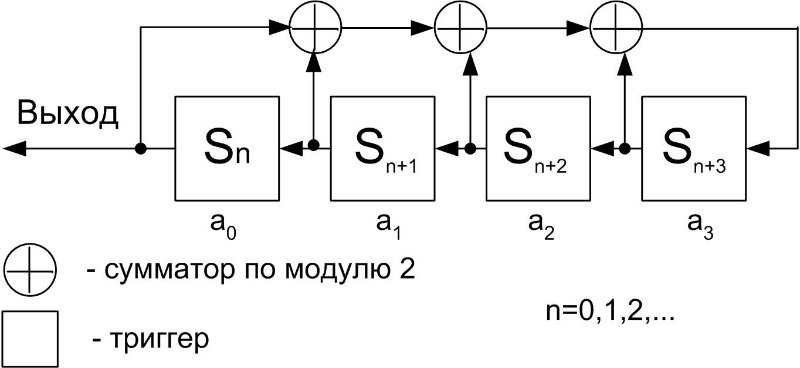 Если какой либо из коэффициентов 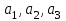 равен нулю, то соответствующий сумматор равен нулю, то соответствующий сумматор  из цепи обратной связи исключается. из цепи обратной связи исключается.Нетрудно видеть, что под действием тактовых импульсов в моменты времени 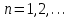 на выходе регистра происходит генерация последовательности на выходе регистра происходит генерация последовательности 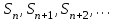 Вектор Вектор 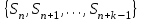 - это вектор n - го состояния регистра. При n=0 вектор - это вектор n - го состояния регистра. При n=0 вектор 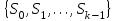 - это вектор начального состояния. - это вектор начального состояния.Характерной особенностью линейных рекуррентных последовательностей над конечным полем является их периодичность в смысле следующего определения. Определение. Пусть S - произвольное непустое множество, и пусть 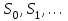 последовательность элементов из множества S. Если существуют целые числа последовательность элементов из множества S. Если существуют целые числа 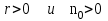 , такие что, , такие что, 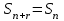 для всех для всех 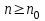 , то последовательность , то последовательность 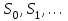 называется периодической последовательностью, а r - периодом этой последовательности. называется периодической последовательностью, а r - периодом этой последовательности.Наименьший из всех возможных периодов называется минимальным периодом. Лемма. Каждый период периодической последовательности делится на ее минимальный период. Определение. Периодическая последовательность 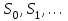 с минимальным периодом r называется чисто периодической, если равенство с минимальным периодом r называется чисто периодической, если равенство 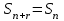 выполняется при всех выполняется при всех 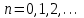 Рассмотрим теперь основные результаты о свойствах периодичности линейных рекуррентных последовательностей над конечными полями, т.к. для криптографических приложений желательно иметь ЛПР с max r . Теорема. Пусть  - произвольное конечное поле, К - некоторое натуральное число. Тогда каждая линейная рекуррентная последовательность К - го порядка над полем - произвольное конечное поле, К - некоторое натуральное число. Тогда каждая линейная рекуррентная последовательность К - го порядка над полем является периодической. При этом ее минимальный период r удовлетворяет неравенству является периодической. При этом ее минимальный период r удовлетворяет неравенству 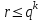 , а в случае однородной последовательности , а в случае однородной последовательности 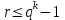 . .Достаточным (но не необходимым) условием чистой периодичности ЛРП является следующее: Теорема. Пусть 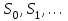 - ЛРП над конечным полем, определяемая рекуррентным соотношением. Если коэффициент - ЛРП над конечным полем, определяемая рекуррентным соотношением. Если коэффициент 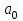 равен 0 т.е. равен 0 т.е. 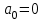 , то последовательность , то последовательность 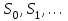 является чисто периодической. является чисто периодической.Из всех однородных линейных рекуррентных последовательностей над полем  удовлетворяющих соотношению К - го порядка, т.е удовлетворяющих соотношению К - го порядка, т.е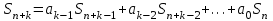 , ,можно выделить одну ЛРП с максимальным значением минимального периода r, которую называют импульсной функцией или ЛРП, порожденной импульсом. Эта последовательность обозначается 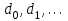 и определяется начальными значениями и определяется начальными значениями 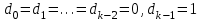 ( (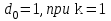 ) и линейным рекуррентным соотношением ) и линейным рекуррентным соотношением 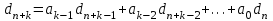 , (n=0,1,…) , (n=0,1,…)Пример: Пусть есть линейное рекуррентное соотношение 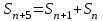 , (n=0,1,…) над полем , (n=0,1,…) над полем 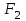 . .Устройство для ее реализации имеет вид: 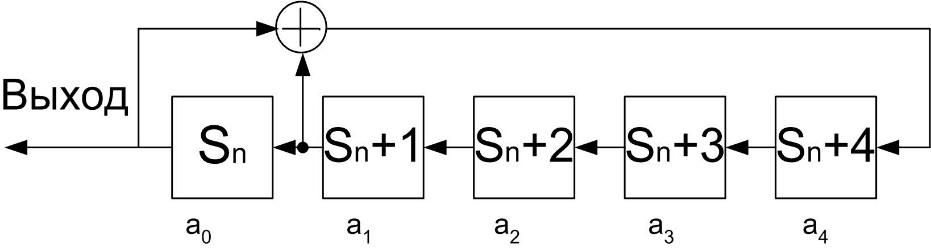 Импульсная функция 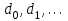 , соответствующая этому рекуррентному соотношению получается при начальном заполнения регистра кодом , соответствующая этому рекуррентному соотношению получается при начальном заполнения регистра кодом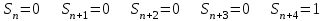 . .Тогда на выходе регистра получим ЛРП, порожденную импульсом с минимальным периодом r=21. Линейные рекуррентные последовательности над конечными полями тесно связаны с рассмотренными нами ранее многочленами. Пусть 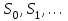 однородная ЛРП К - го порядка над полем однородная ЛРП К - го порядка над полем  , удовлетворяющая рекуррентному соотношению: , удовлетворяющая рекуррентному соотношению: 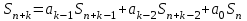 , (n=0,1,…) где , (n=0,1,…) где 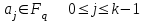 . Многочлен вида . Многочлен вида 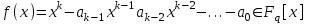 называется характеристическим многочленом данной ЛРП. Его вид зависит только от вида линейного рекуррентного соотношения. называется характеристическим многочленом данной ЛРП. Его вид зависит только от вида линейного рекуррентного соотношения.Пример: Пусть ЛРП над полем 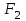 определяется соотношением определяется соотношением 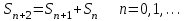 . Тогда соответствующий ей характеристический многочлен имеет вид . Тогда соответствующий ей характеристический многочлен имеет вид 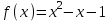 . .Существует прямая связь между периодом ЛРП и порядком характеристического многочлена. Теорема. Пусть 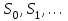 - однозначная на ЛРП над полем - однозначная на ЛРП над полем  и и 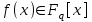 - характеристический многочлен этой последовательности. Тогда линейный период этой последовательности делит - характеристический многочлен этой последовательности. Тогда линейный период этой последовательности делит 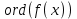 , а минимальный период соответствующей импульсной функции равен , а минимальный период соответствующей импульсной функции равен 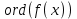 . .Теорема. Пусть 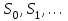 - однородная ЛРП над полем - однородная ЛРП над полем  с ненулевых вектором начального состояния. Пусть ее характеристический многочлен с ненулевых вектором начального состояния. Пусть ее характеристический многочлен 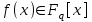 является неприводимым над полем является неприводимым над полем  и удовлетворяет условию и удовлетворяет условию 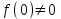 . Тогда ЛРП . Тогда ЛРП 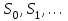 является чисто периодической последовательностью и ее минимальный период является чисто периодической последовательностью и ее минимальный период 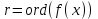 . .Для практических приложений требуется формирование ЛРП с как можно большим минимальным периодом. Каким образом получить такую ЛРП отвечают следующие факты из теории конечного поля (мы уже знаем, что max значение минимального периода не превышает 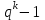 ). ).Определение. Однородная линейная рекуррентная последовательность над полем  , характеристический многочлен который является примитивным над этим полем , характеристический многочлен который является примитивным над этим полем  , а вектор начального состояния - ненулевым вектором, называется последовательностью максимального периода над полем , а вектор начального состояния - ненулевым вектором, называется последовательностью максимального периода над полем  . .Это подтверждает следующая теорема. Теорема. Каждая последовательность К - го порядка и максимального периода над полем  является чисто периодической последовательностью, а её максимальный период равняется является чисто периодической последовательностью, а её максимальный период равняется 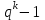 , наибольшему из возможных значений, которое может принимать минимальный период однородной ЛРП К - го порядка над полем , наибольшему из возможных значений, которое может принимать минимальный период однородной ЛРП К - го порядка над полем  . .Пример: Пусть есть рекуррентное соотношение для однородной ЛРП над 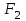 вида: вида: 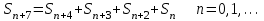 Характеристический многочлен этой ЛРП имеет вид: 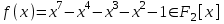 и является примитивным над и является примитивным над 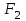 т.е. является нормированным неприводимым над т.е. является нормированным неприводимым над 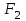 многочленом порядка многочленом порядка 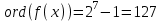 . .Соответствующий регистр сдвига для заданного рекуррентного соотношения будет иметь вид: n=0,1,…  Если в качестве вектора начального состояния регистра взять ненулевой элемент, то, согласно теореме, на его выходе получим последовательность 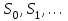 с минимальным периодом 127, т.е. все возможные с минимальным периодом 127, т.е. все возможные 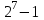 ненулевые векторы встречаются в качестве векторов состояний этой последовательности. При разных начальных ненулевых векторах регистра получим разные ЛРП с одним и тем же периодом 127, но с некоторым сдвигом относительно друг друга. ненулевые векторы встречаются в качестве векторов состояний этой последовательности. При разных начальных ненулевых векторах регистра получим разные ЛРП с одним и тем же периодом 127, но с некоторым сдвигом относительно друг друга.Вектор начального состояния регистра сдвига также можно представить в виде многочлена g(x) степени <К. Тогда, по сути дела, формирование ЛРП обусловлено процедурой деления многочленов 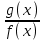 . Следует отметить, что из представленных выше результатов становится понятно, почему криптографы всего мира ищут неприводимые многочлены как можно более высокой степени К (т.к. . Следует отметить, что из представленных выше результатов становится понятно, почему криптографы всего мира ищут неприводимые многочлены как можно более высокой степени К (т.к. 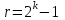 ). Но это NP полная задача и ее решение требует очень больших затрат. В связи с этим в теории конечного поля решены вопросы о том, можно ли осуществить операции почленного сложения или умножения линейных рекуррентных последовательностей, и каким образом это влияет на минимальный период полученной в результате этих операций ЛРП. Пусть - линейная рекуррентная последовательность вида ). Но это NP полная задача и ее решение требует очень больших затрат. В связи с этим в теории конечного поля решены вопросы о том, можно ли осуществить операции почленного сложения или умножения линейных рекуррентных последовательностей, и каким образом это влияет на минимальный период полученной в результате этих операций ЛРП. Пусть - линейная рекуррентная последовательность вида 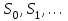 , а , а 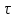 - линейная рекуррентная последовательность вида - линейная рекуррентная последовательность вида 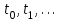 над полем над полем  . Тогда произведением этих последовательностей будки считать последовательность . Тогда произведением этих последовательностей будки считать последовательность 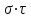 вида вида 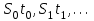 . Аналогично определяется произведение любого числа ЛРП. При таком определении операции произведения ЛРП в теории конечного поля получен ряд важных результатов: . Аналогично определяется произведение любого числа ЛРП. При таком определении операции произведения ЛРП в теории конечного поля получен ряд важных результатов:1. Произведение любого конечного числа линейных рекуррентных последовательностей над полем  само является линейной рекуррентной последовательностью над само является линейной рекуррентной последовательностью над  . .2. Теорема. Пусть 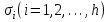 - ЛРП над полем - ЛРП над полем  . И пусть их минимальные периоды равны соответственно . И пусть их минимальные периоды равны соответственно 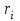 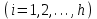 . Тогда если числа . Тогда если числа 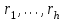 попарно взаимно просты, то минимальный период произведения ЛРП попарно взаимно просты, то минимальный период произведения ЛРП 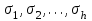 равен произведению равен произведению 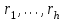 . .Аналогично вводится операция суммирования ЛРП. При этом интересно отметить, что последний результат аналогичен и для операции сложения ЛРП: 3.Теорема. Пусть 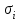 ЛРП над полем ЛРП над полем  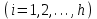 на на 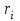 - их минимальные периоды. Тогда если числа - их минимальные периоды. Тогда если числа 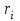 попарно взаимно простые, то минимальный период суммарной последовательности попарно взаимно простые, то минимальный период суммарной последовательности 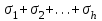 равен произведению равен произведению 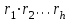 . .Таким образом, суммирование и умножение ЛРП позволяет увеличить их минимальный период. (В этом вопросе есть определенные тонкости математического характера, но о них можно узнать в соответствующей литературе). Для практических приложений весьма важным является вопрос о свойствах линейных рекуррентных последовательностей. Если суммировать все результаты, полученные при исследовании этого вопроса в рамках теории конечного поля и других прикладных дисциплин, то можно сказать следующие: 1. Наиболее важными и интересными свойствами обладают ЛРП максимального периода, формируемые характеристическими многочленами, являющиеся нормированными неприводимыми многочленами над соответствующими полями  . .2.ЛРП максимальной длины имеют равномерный спектр и, следовательно, статистическую равномерность 3. Предельно большая длина периода 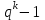 . .4. Отсутствие скрытой периодичности. Отмеченные свойства делают ЛРП эффективным инструментом для создания генераторов псевдослучайных последовательностей, на базе которых строится широкий класс поточных криптосистем. |
