Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
9. Дополнительные математические элементы криптографии. Односторонние функции. Понятие односторонней функции впервые было введено в работе Нидхема (Needham R.M.) о защите входа в вычислительные системы. Определение. Функция 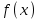 называется односторонней, если для всех x из ее области определения легко вычислить называется односторонней, если для всех x из ее области определения легко вычислить 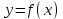 , но почти для всех y из ее области значений нахождение x, для которого , но почти для всех y из ее области значений нахождение x, для которого 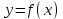 , вычислительно неосуществимо. , вычислительно неосуществимо.В данном определении фраза «почти для всех y» необходима, т.к. можно легко вычислить и запомнить согласно первой части определения целую таблицу значений 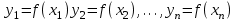 , если окажется, что выбранное значение , если окажется, что выбранное значение 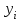 принадлежит этой таблице, то и соответствующий принадлежит этой таблице, то и соответствующий 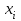 можно легко определить. Фраза «вычислительно неосуществимо» означает с точки зрения теории сложности, что неосуществимо за полиномиальное время, которое характеризует решаемые задачи. можно легко определить. Фраза «вычислительно неосуществимо» означает с точки зрения теории сложности, что неосуществимо за полиномиальное время, которое характеризует решаемые задачи.До сих пор не доказано, что односторонние функции существуют. Показано, что проблема существования односторонних функций эквивалентна известной нерешенной проблеме совпадения задач классов Р и NP. Тем не менее, предложено много функций, которые похожи на односторонние. В качестве возможной односторонней функции Дж. Гилл предложил использовать показательную функцию следующего вида: 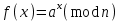 , где , где 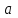 - (основание) принадлежит интервалу (1, n-1), а умножение ведется по модулю n. Значение - (основание) принадлежит интервалу (1, n-1), а умножение ведется по модулю n. Значение 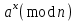 вычисляется достаточно эффективно с помощью известной схемы Горнера «слева на право» вычисляется достаточно эффективно с помощью известной схемы Горнера «слева на право»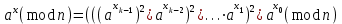 или «справа налево» 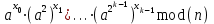 для числа x при его двоичном разложении в виде 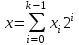 . .Даже при больших числах x из интервала (1, n) вычисление 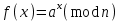 можно осуществить за можно осуществить за 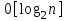 операций. Обратная к этой функции - операция вычисления дискретного логарифма x: по данным операций. Обратная к этой функции - операция вычисления дискретного логарифма x: по данным 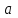 и y найти такое целое x, что и y найти такое целое x, что 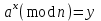 . До настоящего времени не известно эффективных алгоритмов решения этой задачи. Известно лишь, что сложность вычисления дискретного логарифма x эквивалента сложности разложения целого числа на произведение простых чисел и оценивается как . До настоящего времени не известно эффективных алгоритмов решения этой задачи. Известно лишь, что сложность вычисления дискретного логарифма x эквивалента сложности разложения целого числа на произведение простых чисел и оценивается как 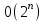 ,т.е. экспоненциальная оценка временной сложности. ,т.е. экспоненциальная оценка временной сложности.На основе такой показательной односторонней функции Диффори и Хеллман разработали так называемую криптографическую схему открытого распределения ключей, о которой более подробно поговорим на следующих лекциях. В качестве односторонней функции Кнут Д. предложил использовать функцию вида 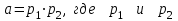 простые числа. Идея здесь заключается в том, что произведение двух простых чисел вычислить достаточно просто, а вот разложение числа простые числа. Идея здесь заключается в том, что произведение двух простых чисел вычислить достаточно просто, а вот разложение числа 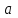 на сомножители на сомножители 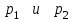 достаточно трудная задача. достаточно трудная задача.В ряде случаев в качестве односторонней функции предлагается использовать известную задачу о рюкзаке. Напомним, что эта задача имеет следующую формировку: дано множество n целых чисел 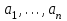 и целое число S, требуется определить существует - ли множество чисел и целое число S, требуется определить существует - ли множество чисел  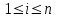 , такое что их сумма равна числу S. Эта задача принадлежит к числу NP полных задач и имеет экспоненциальную временную сложность , такое что их сумма равна числу S. Эта задача принадлежит к числу NP полных задач и имеет экспоненциальную временную сложность 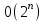 . .Следует отметить, что использование односторонних функций в чистом виде для зашифрования информации не имеет смысла, так как никто, даже законный адресат не сможет расшифровать шифротекст 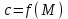 , полученный с ее помощью. Однако идея, лежащая в основе построения таких функций, может быть использована для построения так называемых односторонних функций с секретом, которые уже имеют практический смысл. , полученный с ее помощью. Однако идея, лежащая в основе построения таких функций, может быть использована для построения так называемых односторонних функций с секретом, которые уже имеют практический смысл.Рассмотрим принципы построения односторонних функций с секретом на примере степенной функции вида 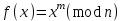 . .Определение. Односторонней функцией с секретом называется зависящая от параметра К функция 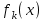 , такая, что при известном К можно найти полиномиальные алгоритмы , такая, что при известном К можно найти полиномиальные алгоритмы 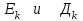 , позволяющие легко вычислить как , позволяющие легко вычислить как 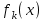 , так и обратную к ней функцию , так и обратную к ней функцию 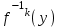 для всех x из области определения функции для всех x из области определения функции 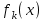 . При этом нахождение . При этом нахождение 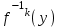 вычислительно неосуществимо без знания секретного параметра К даже при известном алгоритме вычислительно неосуществимо без знания секретного параметра К даже при известном алгоритме  . .Степенная функция 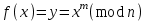 достаточно легко, за достаточно легко, за 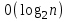 операций может быть вычислена при известных m и n. Преобразование возведения в степень операций может быть вычислена при известных m и n. Преобразование возведения в степень 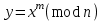 называется вычислением корня m степени по модулю n. В настоящее время вычисление такого x, что называется вычислением корня m степени по модулю n. В настоящее время вычисление такого x, что 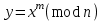 при известных y,m,n относится классу трудных задач. Основная идея использования односторонних функций с секретом сводится к следующему. при известных y,m,n относится классу трудных задач. Основная идея использования односторонних функций с секретом сводится к следующему.Получение шифрованного текста С из исходного текста М осуществляется путем использования указанной степенной функции в виде: 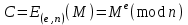 , где e,n - ключ преобразования зашифрования. , где e,n - ключ преобразования зашифрования.При расшифровании открытый текст M восстанавливается путем использования преобразования расшифрования на базе этой же функции но с другой степенью d в качестве ключа:  . Оба эти преобразования легко выполнить за . Оба эти преобразования легко выполнить за  операций. операций.Если теперь ключ (e, n) преобразования зашифрования сделать открытым, а параметр d держать в секрете, то восстановление исходного текста M из зашифрованного текста С даже при известном алгоритме зашифрования потребует решения трудной задачи вычисления функции обратной к функции зашифрования т.е. вычисления корня степени e по модулю n. Это позволяет использовать принцип открытого шифрования, когда преобразование расширения держится в секрете. В этом случае (e,n) - открытый ключ, а - (d,n) - секретный ключ. Более подробно мы рассмотрим этот вопрос при описании блочной криптосистемы RSA. Группы подстановок. При построении криптографических систем широкое применение получили так называемые перестановочные многочлены конечных полей  , которые индуцируют перестановки элементов конечного поля , которые индуцируют перестановки элементов конечного поля  и, следовательно, соответствуют элементам симметрической группы и, следовательно, соответствуют элементам симметрической группы  , т.е. группы всех подстановок на множестве из q элементов. , т.е. группы всех подстановок на множестве из q элементов.Дадим определение перестановочного многочлена конечного поля  и приведем ряд теорем, позволяющих выяснить является ли данный многочлен перестановочным или нет. и приведем ряд теорем, позволяющих выяснить является ли данный многочлен перестановочным или нет.Определение. Многочлен  называется перестановочным многочленом поля называется перестановочным многочленом поля  , если соответствующая ему полиномиальная функция , если соответствующая ему полиномиальная функция  , отображающая элемент поля , отображающая элемент поля  в элемент в элемент  , является перестановкой элементов поля , является перестановкой элементов поля  . .Если  является перестановочным многочленом, то, очевидно, для каждого элемента является перестановочным многочленом, то, очевидно, для каждого элемента  уравнение уравнение  имеет одно решение в поле имеет одно решение в поле  . .Заметим, что операция приведения некоторого многочлена g(x) по модулю  обозначается обозначается  и ее результатом является остаток и ее результатом является остаток  от деления от деления  на на  . .Тогда можно установить критерий того, что данный многочлен является перестановочным. Для этого потребуется следующая лемма. Лемма. Пусть  элементы поля элементы поля  . Тогда следующие два условия эквивалентны: . Тогда следующие два условия эквивалентны:1. 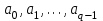 все различны; все различны;2. 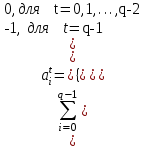 . .С учетом этой леммы можно получить критерий Эрмита, того, что данный многочлен является перестановочным. Критерий Эрмита. Пусть р - характеристика поля  . Тогда многочлен . Тогда многочлен 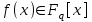 является перестановочным многочленом поля является перестановочным многочленом поля  в том и только в том случае, если выполняются следующие два условия: в том и только в том случае, если выполняются следующие два условия:1. Многочлен 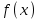 имеет ровно один корень в имеет ровно один корень в  . .2. Для каждого целого t, такого, что  , результат приведения многочлена , результат приведения многочлена  по модулю по модулю  имеет степень имеет степень  . . Отсюда вытекает важное следствие: Если число 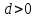 является делителем числа q -1, то над полем является делителем числа q -1, то над полем  не существует перестановочного многочлена степени d. не существует перестановочного многочлена степени d.В теории конечного поля имеются и другие критерии того, что данный многочлен является перестановочным и с ними можно ознакомится в соответствующей литературе. Пользуясь критерием Эрмита, можно получить все перестановочные многочлены произвольной фиксированной степени поля  . .Примеры перестановочных многочленов можно получить на основе следующего простого результата. Теорема: 1. Каждый линейный многочлен над полем  является перестановочным многочленом поля является перестановочным многочленом поля  . .2. Одночлен 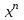 является перестановочным многочленом поля является перестановочным многочленом поля  тогда и только тогда, когда тогда и только тогда, когда 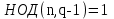 (т.е. число n и q -1 взаимно просты). (т.е. число n и q -1 взаимно просты).Например, 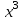 - перестановочный многочлен поля - перестановочный многочлен поля  , если , если  т.е. т.е.  . .Перестановочные многочлены поля  , имеющие степень меньшую чем q, можно комбинировать друг с другом с помощью операции композиции с последующим приведением по модулю , имеющие степень меньшую чем q, можно комбинировать друг с другом с помощью операции композиции с последующим приведением по модулю  . Эту операцию обозначают . Эту операцию обозначают  и под ней понимают и под ней понимают 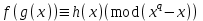 . .Множество перестановочных многочленов поля  , степень которых меньше q, образуют группу относительно операции композиции. Эта группа изоморфна симметрической группе , степень которых меньше q, образуют группу относительно операции композиции. Эта группа изоморфна симметрической группе 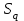 , т.е. группе всех перестановок на множестве из q элементов. Таким образом, симметрическую группу , т.е. группе всех перестановок на множестве из q элементов. Таким образом, симметрическую группу 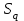 , перестановок и ее подгруппы можно представить в виде групп перестановочных многочленов. , перестановок и ее подгруппы можно представить в виде групп перестановочных многочленов.Например: Теорема. Если q>2, то многочлен 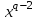 вместе с линейными многочленами над полем вместе с линейными многочленами над полем  порождает симметрическую группу подстановок порождает симметрическую группу подстановок  . .Математические элементы теории перестановочных многочленов над конечными полями и индуцируемых ими групп подстановок находит применения при построении блочных криптосистем для перестановки информационных блоков передаваемых сообщений. Хеш-функции. Термин хеш-функция (или функция хеширования) возник в теории сложности вычислений, где он обозначал функцию, которая сжимает строку чисел произвольного размера в строку чисел фиксированного размера. Это понятие использовалось в алгоритмах поиска данных по значениям хеш-функции от них. Рассмотрим это понятие применительно к криптографии. Криптографические хеш-функции делятся на два класса: с ключом и без ключа. Значение хеш-функции с ключом может вычислить лишь тот, кто знает некоторый секретный параметр - ключ. В литературе она еще называется МАС - кодами аутентификации сообщений. Определение. Хеш-функцией с ключом (зависящей от ключа) называется функция, имеющая следующие свойства: 1. Описание функции Н(k,x) должно быть открыто, а секретная информация должна содержаться только в выборе ключа k (правило Керкхофа). 2. Аргумент х функции Н(k,x) может быть строкой чисел произвольной длины, а значение функции должно быть строкой чисел фиксированной длины. 3. При любых данных k и х вычисление Н(k,x) должно быть быстрым (за полиномиальное время) 4. По любому данному х должно быть трудно угадать значение Н(k,x) с вероятностью большей, чем  , где n - число бит в выходной строке. Должно быть трудно определить ключ k даже по большему числу известных пар , где n - число бит в выходной строке. Должно быть трудно определить ключ k даже по большему числу известных пар  или вычислить по этой информации Н(k,x’)для x’xi. или вычислить по этой информации Н(k,x’)для x’xi.Хеш-функция без ключа называется МДС - код определения манипуляции. Эти функции делятся на два класса: слабые односторонние хеш-функции и сильные односторонние хеш-функции. Определение. Односторонней слабой хеш-функцией называется функции Н(х), удовлетворяющая условием: 1. Аргумент х функции может быть строкой чисел произвольного размера 2. Значение функции Н(х) представляет собой строкой фиксированного размера 3. Значение функции Н(х) легко вычисляется (за полиномиальное время) 4. Почти для всех y вычислительно невозможно найти такое х что Н(х)=y 5. Для любого фиксированного х вычислительно невозможно найти другое x’x такое, что  . Такое событие, т.е. . Такое событие, т.е.  называется коллизией. называется коллизией.Свойства 3 и 4 утверждают, что  является односторонней функцией. По свойствам 1 и 2 коллизии должны существовать, однако свойство (5) требует, чтобы найти их было вычислительно невозможно. является односторонней функцией. По свойствам 1 и 2 коллизии должны существовать, однако свойство (5) требует, чтобы найти их было вычислительно невозможно.Определение. Односторонней сильной хеш-функцией  является функция, удовлетворяющая свойством 1 - 4 предыдущего определения, а свойств 5 заменяется следующим. является функция, удовлетворяющая свойством 1 - 4 предыдущего определения, а свойств 5 заменяется следующим.5. Вычислительно невозможно найти любую пару аргументов  такую, что такую, что  . Оба определения предполагают выполнение правила Керкхофа , т.е. описание функции . Оба определения предполагают выполнение правила Керкхофа , т.е. описание функции  открыто. открыто.Применение криптографических хеш-функций исключительно разнообразно и одним из основных их применений являются схемы и алгоритмы цифровой подписи сообщений. Об этом мы поговорим ниже. |
