Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
5. Элементы теории конечного поля. Основные понятия и теоремы. Поле. Определение. Отображение : RS кольца R в кольцо S называется гомоморфизмом, или для любых a,b R (a+b)= (a)+ (b) и (ab)= (a)(b). Таким образом, гомоморфизм : RS сохраняет обе операции + и . кольца R. Определение. Для простого числа Р обозначим через FP множества {0,1,2,...,P -1} целых чисел, и пусть отображение : Z/pFp определяется условием ([a])=a для a=0,1,2,...,P -1. Тогда множество FP со структурой поля, индуцированной отображением , называется полем Галуа порядка P. (Такое поле еще обозначают GF(p) – аббревиатура от слов Galois и Field(поле)). Отображение : Z/pFp является изоморфизмом т.к. ([a]+[b])= ([a])+ ([b]) и ([a][b])= ([a])([b]). Нулем конечного поля GFp будет 0 ноль, а единицей – единица 1 и его структура совпадает со структурой поля Z/p. Пример. Важным является пример конечного поля GFp второго порядка. Элементами этого поля являются 0 и 1 - бинарные элементы, для которых выполняются операции
В связи с использованием для вычислений ЭВМ не менее важным является поле Галуа из элементов {0,1}, обозначаемое GF(2N) и соответствующие строкам данных длиной N бит. Такие строки бит удобно рассматривать в виде многочленов. Например, байт из 8 бит можно представить (10010101)=x7+x4+x2+1. Определение. Пусть R произвольное кольцо. Если существует такое натуральное число n, что для каждого rR выполняется равенство nr=0, то наименьшее из таких чисел n (например, n0) называется характеристикой кольца R, а само R называют кольцом характеристики n0. Теорема. Если кольцо R{0} с единицей е и без делителей нуля имеет положительную характеристику n, то n – простое число. Следствие. Характеристикой конечного поля является простое число. Теорема. Пусть R – коммутативное кольцо простой характеристики p. Тогда 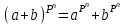 ; ; 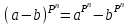 ; ; 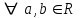 и и 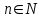 . .Выясним теперь, каким должен быть идеал М коммутативного кольца R с единицей, чтобы фактор -кольцо R/M было полем. Пусть R – коммутативное кольцо с единицей. Элемент aR называется делителем элемента bR, если существует элемент сR такой, что ас=b. Делители единицы 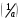 называются обратимыми элементами a -1. Элементы a и b из R называют ассоциированными, если обратимый элемент rR такой, что a=br. Элемент cR называется простым элементом кольца R, если он не является обратимым элементом и не имеет других делителей, кроме ассоциированных с ним элементов или обратимых элементов. Идеал pR кольца R называют простым идеалом, если для a,bR включение abP имеет место лишь в том случае, когда либо aP, либо bP. Идеал MR кольца R называется максимальным идеалом, если идеала J кольца R включение называются обратимыми элементами a -1. Элементы a и b из R называют ассоциированными, если обратимый элемент rR такой, что a=br. Элемент cR называется простым элементом кольца R, если он не является обратимым элементом и не имеет других делителей, кроме ассоциированных с ним элементов или обратимых элементов. Идеал pR кольца R называют простым идеалом, если для a,bR включение abP имеет место лишь в том случае, когда либо aP, либо bP. Идеал MR кольца R называется максимальным идеалом, если идеала J кольца R включение 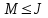 влечет за собой J=M или J=R. Кольцо R называют кольцом главных идеалов, если оно является целостным кольцом, и каждый идеал J кольца R является главным, т.е. элемент aR такой, что J=(a)={rarR}. влечет за собой J=M или J=R. Кольцо R называют кольцом главных идеалов, если оно является целостным кольцом, и каждый идеал J кольца R является главным, т.е. элемент aR такой, что J=(a)={rarR}.Как уже указывалось на прошлых лекциях, важную роль в криптографических приложениях играют многочлены и наиболее важные и интересные результаты по ним получены в теории конечного поля. Напомним, что многочленом называется выражение вида 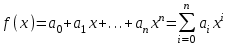 , ,где n – целое неотрицательное число – степень многочлена, ai – элементы кольца (коэффициенты многочлена), x – переменная или неизвестная не принадлежащая кольцу. Следует отметить, что при обычном определении многочлена связь между коэффициентами ai и переменной x обычно не обсуждается. Однако такая связь существует и возможно ее показать в рамках абстрактной алгебры, давая определение многочлена как элемента кольца многочленов. Определение. Кольцо S, образованное многочленами над кольцом R, называется кольцом многочленов над R и обозначается R[x]. Рассмотрим множество S всех бесконечных последовательностей вида (a0,a1,...,an,...), компонентами ai которого является элементы коммутативного кольца R с единицей 1, причем лишь конечное число компонент ai может быть отлично от 0. Это множество образует коммутативное кольцо с единицей относительно операций + и . Кольцо R таким образом можно рассматривать как подкольцо кольца S, а S – как расширение кольца R. Элементами кольца S являются многочлены 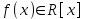 , определяемые как бесконечные последовательности с конечным числом ненулевых элементов. , определяемые как бесконечные последовательности с конечным числом ненулевых элементов.При этом переход от кольца R к кольцу многочленов S над R называется кольцевым присоединением элемента x к кольцу R. Таким образом, отображается связь между элементами кольца R (коэффициентами многочлена ai) и новым элементом x. В дальнейшем изложении в основном будем иметь дело с многочленами над полями F, поэтому для кольца многочленов над полем F будем использовать обозначение F[x] или G F[x]. Для кольца многочленов над полем справедливы операции +, , сравнения, деления с остатком, делимость: Два многочлена 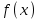 и и 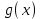 F[x] над полем F считаются равными тогда и только тогда, когда F[x] над полем F считаются равными тогда и только тогда, когда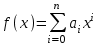 , , 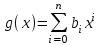 , и , и 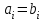 для для 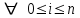 . .Сумма многочленов 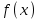 и и 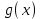 определяется равенством определяется равенством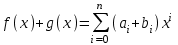 , ,а произведение многочленов 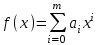 и и 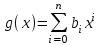 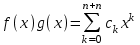 , , 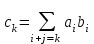 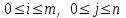 . .Деление: многочлен g(x)F[x] делит многочлен f(x)F[x] если существует h(x)F[x] такой, что f(x)=g(x)h(x). Деление с остатком. Пусть g(x)0 – многочлен из F[x] над полем F. Тогда для каждого f(x)F[x] существуют такие многочлены q(x) и r(x) F[x], что f(x)=q(x)g(x)+r(x) (deg(r) Простые элементы кольца многочленов F[x] обычно называют неприводимыми многочленами. Определение: Многочлен f(x)F[x] называется неприводимым над полем F или в кольце F[x], если он имеет положительную степень и равенство f(x)=g(x)h(x); g(x),h(x)F[x] может выполнятся лишь в том случае, когда либо g(x), либо h(x) являются постоянными многочленами (т.е. имеют степень 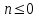 и являются константами). и являются константами).Неприводимость многочлена существенным образом зависит от того, над каким полем он рассматривается. Примеры: Многочлен f(x)=x2 -2 Q неприводим над полем рациональный чисел Q, но приводим над полем действительных чисел R т.к. 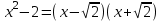 . .Многочлен f(x)=x2+x+1 неприводим над полем Галуа GF(r) т.к. f(0)=f(1)=1, но приводим над его расширением GF(4). Неприводимые многочлены играют важную роль в устройстве кольца, т.к. каждый многочлен из F[x] может быть представлен, причем единственным способом, в виде произведения неприводимых многочленов. Эти неприводимые многочлены являются, по сути дела, аналогами простых чисел, через произведение которых можно выразить любое натуральное число n>1 (основная теорема арифметики). В нашем дальнейшем изложении применительно к криптосистемам особенный интерес будут представлять многочлены неприводимые степени n над простыми полями Fp порядка p, где p – простое число. Поиск всех неприводимых многочленов заданной степени n над некоторым полем Fp или GF(p) представляет собой очень сложную задачу. Французский математик Эварист Галуа (1811 -1832гг) создал теорию (теорию поля Галуа), доказывающую существование неприводимых многочленов сколь угодно большой степени, но поиск таких многочленов - очень сложная задача, и криптографические службы всего мира ведут активную работу по поиску таких многочленов, но эти работы засекречены. Известен неприводимый многочлен степени x61+ x3+1, а для n>61 данных найти не удалось. Чтобы более подробно осветить вопросы нахождения неприводимых многочленов над конечными полями, вопросы разложения многочленов на множители над конечными полями и связанные с ними проблемы построение линейных рекуррентных последовательностей над конечными полями, которые лежат в основе построения современных криптосистем, продолжим знакомство с основными понятиями и элементами теории конечного поля. Определение. Пусть F – произвольное поле и f(x)F[x]. Тогда замена переменной x в многочлене f(x) произвольным элементом bF обращает этот многочлен в корректно определенный элемент поля F. Если f(x)=a0+a1x+...+anxnF[x] и bF, то, заменяя x на b, получаем элемент f(b)=a0+a1b+...+anbnF. Элемент f(b) называют значением многочлена f(x) при x=b. Если в кольце F[x] имеется какое -либо полиномиальное равенство, то заменяя в нем x на bF, получаем равенство в поле F. (Принцип подстановки). Тогда: элемент bF называют корнем (или нулем) многочлена f(x)F[x], если при x=b f(b)=0. Теорема (устанавливает связь между корнями и делимостью). Элемент bF является корнем многочлена f(x)F[x] тогда и только тогда, когда многочлен x -b делит f(x) (т.е. x -bf(x)). Определение. Пусть bF - корень многочлена f(x)F[x]. Кратностью корня b называют такое натуральное число K=(1,2,...), что f(x) делится на (x -b)K , но не делится на (x -b)K+1. При K=1 корень называют простым, а при K>1 – кратным. Определение. Производной многочлена f(x)=a0+a1x+a2x2+...+anxnF[x] называется многочлен f’(x)=a1+2a2x+...+nanxn -1F[x]. Отсюда следует теорема. Теорема. Корень bF многочлена fF[x] является кратным тогда и только тогда, когда он одновременно является и корнем производной f’(x) многочлена f(x). Существует связь между отсутствием или несуществованием корней и неприводимостью многочленов. Если f(x) - неприводимый многочлен из F[x] степени n2, то согласно теореме он не имеет корней в поле F. Обратное утверждение справедливо только для многочленов степени 2 и 3. Теорема. Для неприводимости многочлена f(x)F[x] степени 2 и 3 в кольце F[x] необходимо и достаточно, чтобы он не имел корней в поле F. Пример: Пользуясь этой теоремой, можно найти неприводимые многочлены степени 2 и 3 в кольце F2[x] над конечным полем F2, путем исключения из всей совокупности многочленов указанной степени, принадлежащих кольцу F2[x], тех многочленов, которые имеют корни в поле F2. Напомним, что элементами поля F2 или GF(r) являются {0,1}. Тогда очевидно, что в кольце F2[x] имеется только один неприводимый многочлен степени 2: f(x)=x2+x+1 и два неприводимых многочлена степени 3: f(x)=x3+x+1, x3+x2+1. Действительно: многочлены степени 2 – это f1=x2+1, f2=x2+x, f3=x2+x+1. Подставляя в них вместо x элементы в поля GF(r), т.е. 0 или 1, видно, что f1=0 при x=1, f2=0 при x=1 и x=0, а f30 при любом x{0,1}. Тоже самое и для многочленов степени 3: f1=x3+x2+x+1, f2=x3+x2+1, f3=x3+x+1, f4=x3+x2+x, f5=x3+x2… Наряду с многочленами f(x) от одной переменной х, рассматривают многочлены от нескольких переменных. Пусть R - коммутативное кольцо с единицей, и пусть х1,...,хn символы, которые выступают в качестве переменных, образуем сначала кольцо многочленов R[x1], затем кольцо R[x1,x2]=R[x1]R[x2] и т.д. пока не получим R[x1,...,xn]=R[x1,...,xn -1]R[xn]. Элементами кольца R[x1,...,xn] являются выражения f(x1,...,xn)= 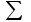 ai1...inx1i1...xnin ai1...inx1i1...xninс коэффициентами аi1...inR, причем суммирование распространяется на конечное множество n наборов (i1,...,in) неотрицательных целых чисел и соблюдается соглашение xj0=1, 1jn. Такое выражение называют многочленом от переменных х1,...,хn над кольцом R. Два многочлена f и g из R[x1,...,xn] равны, когда равны все соответствующие коэффициенты. При этом предполагается, что переменные х1,...,хn перестановочны друг с другом, так что, например, выражения x1 х2 х3 и х3 х1 х2 отождествляются. |
