Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
Для n=0 Z имеем a0 = e в мультипликативных обозначениях и 0а=0 в аддитивных обозначениях. Группы G, использующие указанные формы записи называют мультипликативными и аддитивными. Примеры. Пусть G - множество целых чисел с операцией + (сложение). Известно, что данная операция, т.е. сумма двух целых чисел однозначно определяет целое число. Эта группа G, единичным элементом которой является 0, а обратным для целого числа а является число -а . Такую группу обозначают через Z. Множество, состоящее из единственного элемента е с операцией * , определенной условием е*е=е является группой. Определение. Мультипликативная группа G называется циклической, если в ней имеется такой элемент а , что каждый элемент b G является степенью элемента а т.е. существует целое число К такое, что b = aK. Этот элемент а называется образующим элементом группы G . Для циклической группы G применяют обозначение G=<а>. Из определения следует, что циклическая группа является коммутативной или абелевой. В аддитивной циклической группе Z b=ка может быть более одного образующего элемента, например 1 и –1. Отношением эквивалентности на множестве S называется подмножество R множества SS упорядоченных пар (s,t) s,tS обладающее тремя свойствами: 1. (s,s) R для всех sS (рефлективностью) 2. Если (s,t) R , то (t,s) R (симметричностью) 3. Если (s,t) ,(t,v) R, то (s,v) R (транзитивностью) Элементы s,tS называются эквивалентными, если (s,t)R. Простейшим примером отношения эквивалентности является равенства s=t: s=s, t=t R s=t t=s R s=t, t=v s=v R Отношение эквивалентности на множестве S разбивает это множество S на попарно непересекающиеся подмножества, объединяя все элементы множества S, эквивалентные некоторому фиксированному элементу sS получим класс эквивалентности элемента s, который обозначается: [s]={tS(s,t) R}. Совокупность всех различных классов эквивалентности дает указанное выше разбиение множества S на попарно непересекающиеся подмножества (классы эквивалентности). Как уже отмечалось на прошлой лекции, важным классом эквивалентности на множестве целых чисел является отношение сравнимости чисел а и b (a,b z) по модулю n. ab(modn). Классы эквивалентности, на которые отношение сравнимости по модулю n разбивает множество целых чисел Z, называют классами вычетов по модулю n. Ими являются: [0]={..., –2n; -n, 0, n, 2n, ...} [1]={..., -2n+1, -n+1, 1, n+1, 2n+1, ...} [n -1]={..., -n -1, -1, n -1, 2n -1, 3n -1, ...} Определение. Группа, образованная множеством { [0], [1], ... ,[n -1]} классов вычетов по модулю n с операцией [a]+[b]=[a+b], называется группой классов вычетов по модулю n и обозначается Zn. Группа Zn является циклической с образующим элементом [1] и имеет порядок n. Определение. Группа называется конечной (бесконечной), если она состоит из конечного (бесконечного) числа элементов. Число элементов конечной группы G называется ее порядком и обозначается G. Удобным способом задания конечной группы является их представление в виде таблицы групповой операции (таблицы Кэли), которая строится так: ее строки и столбцы помечаются элементами группы и на пересечении строки, помеченной элементом а и столбца, помеченного элементом b, ставится элемент аb. Пример: Таблица Кэли группы Z6 классов вычетов по модулю 6.
Эта группа Z6 представляет собой: Пусть G - множество остатков {0, 1, 2, 3, 4, 5} от деления целых чисел из Z на 6 и для чисел а и b из G величина а*b пусть остаток от деления на 6 обычной суммы а + b. Тогда получим группу Z6. Каждая группа содержит некоторые подмножества , которые сами образуют группу с той же групповой операцией. Определение. Подмножества Н группы G называется подгруппой этой группы, если Н само образует группу относительно операций группы. Примером группы является следующее определение. Определение. Подгруппа группы G,состоящая из всех степеней элемента а этой группы, называется подгруппой, порожденной элементом а и обозначается <а>. Если подгруппа <а> конечна, то ее порядок называется порядком элемента а. а1, а2, ... аn. Приведем следующую теорему, доказательство которой тривиально. Теорема. Если Н - подгруппа группы G, то отношение RH на G определяемое условием (а,b)R↔a=bh для некоторого hH, является отношением эквивалентности. Соответствующие отношению Rn классы эквивалентности называются левыми смежными классами группы G по подгруппе H и обозначаются aH={ahh H} для мультипликативной группы или a + H ={a+hh H} для аддитивной группы где а – фиксированный элемент группы G. Аналогично определяется разбиение группы G на правые смежные классы по подгруппе H Ha={hahH}. Если G – абелева группа, то ее левые смежные классы по подгруппе H совпадают с правыми, а сама подгруппа Н нормальная. Пример. Пусть G12={[0],[1],[2],...,[11]} и пусть H подгруппа H={[0],[3],[6],[9]}. Тогда различными (левыми) смежными классами G по H являются [0] + H = {[0],[3],[6],[9]} [1] + H = {[1],[4],[7],[10]} [2] + H = {[2],[5],[8],[11]}. Теорема. Если H - конечная подгруппа группы G, то каждый (левый или правый) смежный класс группы G по подгруппе H содержит столько же элементов, сколько H. Определение. Если подгруппа H группы G такова, что множество смежных классов G по H конечно, то число этих смежных классов называется индексом подгруппы H в группе G и обозначается (G:H). Так как левые смежные классы группы G по подгруппе H образуют разбиение этой группы, то из указанной выше теоремы вытекает следующий важный результат. Теорема. Порядок конечной группы G равен произведению порядка любой её подгруппы H на индекс (G:H) этой подгруппы в G. В частности, порядок любой подгруппы H группы G и её индекс в G делят порядок группы G. Порядок любого элемента aG делит порядок группы G. Результаты относящиеся к подгруппам и порядкам элементов для циклических групп можно обобщить следующей теоремой Теорема 1. Каждая подгруппа циклической группы также является циклической. 2. В конечной циклической группе порядка m элемент aK порождает подгруппу порядка 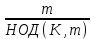 . .3. Если d положительный делитель порядка m конечной циклической группы , то содержит единственную подгруппу индекса d. Для любого положительного делителя l числа m группа содержит в точности одну подгруппу порядка l. 4. Пусть l положительный делитель порядка конечной циклической группы . Тогда содержит (l) элементов порядка l. (Напомним, что (l) – функция Эйлера: число целых чисел K 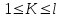 , взаимно простых с числом l). , взаимно простых с числом l).5. Конечная циклическая группа порядка m содержит (m) образующих (т.е. таких элементов ar, что В большинстве числовых систем, используемых в элементарной арифметике, имеются две различные бинарные операции: сложение и умножение. Примерами могут служить целые, рациональные и действительные числа. Поэтому в абстрактной алгебре были введены алгебраические структуры, которые обладают основными свойствами указанных числовых систем. К таким алгебраическим структурам относятся кольца и поля. Кольца. Поля. Определение. Кольцом R называется множество R с двумя бинарными операциями, обозначаемыми + или такими, что: R – абелева группа относительно операции + (т.е. выполняется коммутативный закон сложения a+b=b+a) Операция ассоциативна т.е. для любых a, b, c R (a b) c = a (b c) Выполняются законы дистрибутивности: a, b, c R справедливо a (b + c) = ab + ac; (b + c) a = ba + ca. Здесь операции + и не обязательно являются обычным сложением и умножением. Единичный элемент аддитивной группы кольца K называется нулем и обозначается 0, а обратный к элементу a этой группы обозначают –a. Для кольца выполняются по определению свойства: a 0 = 0 a = 0 длявсех a R ( -a) b = a ( -b) = -ab длявсех a,b R. Кольцо называется кольцом с единицей, если оно имеет мультипликативную единицу, т.е. существует такой элемент e R, что a e = e a = a для всех a R Кольцо называется коммутативным, если операция коммутативна a b = b a Кольцо называется целостным кольцом (или областью целостности), если оно является коммутативным кольцом с единицей e 0, в котором равенство a b = 0 влечет за собой a=0 или b=0. Кольцо R называется телом если R {0} и ненулевые элементы в R образуют группу относительно операции . Другими словами тело – это кольцо с единицей, в котором для каждого элемента a 0 существует обратный по умножению элемент a -1 такой, что a(a -1)=1. Полем называется тело, операция в котором коммутативна, т.е. ab = ba Поскольку основной алгебраической структурой, которая будет использоваться в дальнейшем, является поле, рассмотрим более подробно его определения. Поле есть множество F на котором заданы две операции, называемые сложением + и умножением , и которое содержит два выделенных элемента 0 и е, причем 0 е. Поле это абелева группа по сложению, единичным элементом которой является 0, а элементы из F отличные от нуля, образуют абелеву группу по умножению, единичным элементом которой является е. Операции сложения и умножения в поле связаны законом дистрибутивности a(b+c)=ab+ac. Второй закон дистрибутивности (b+c)a=ba+ca выполняется автоматически в силу коммутативности операции умножения. Элемент 0 называется нулевым, а элемент е – единицей т.е. е=1. Свойство поля, появляющееся из определения целостности кольца, т.е. равенство ab=0 влечет a=0 или b=0, выражают словами «отсутствуют делители нуля». Другими словами в коммутативном кольце ненулевой элемент а называют делителем нуля, если существует другой ненулевой элемент b такой, что ab=0. Если в кольце нет делителей нуля, то оно называется кольцом без делителей нуля или областью целостности. Никакой делитель нуля не может иметь обратного по умножению элемента. Поэтому никакое поле и тело не содержат делителей нуля. Определение. Подмножество S кольца R называется подкольцом этого кольца, если оно замкнуто относительно операций + и и образует кольцо относительно этих операций. (Замкнутость - это условие когда результат операций a+b и ab над a,bS также S). Определение. Подмножество J кольца R называется идеалом этого кольца, если оно является подкольцом кольца R и для всех aJ и rR имеет место arJ, raJ. Например. Пусть R - поле рациональных чисел (вида 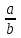 , , 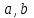 - целые числа, - целые числа, 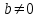 ). Тогда множество целых чисел Z (вида –n,n,0, n – целые числа >0) является его подкольцом, но не идеалом т.к., например a=1Z, r=1/2 R, но ar=11/2=1/2 Z. ). Тогда множество целых чисел Z (вида –n,n,0, n – целые числа >0) является его подкольцом, но не идеалом т.к., например a=1Z, r=1/2 R, но ar=11/2=1/2 Z.Так как идеалы являются нормальными (левые смежные классы совпадают с правыми) подгруппами аддитивной группы кольца, то каждый идеал J кольца R определяет некоторое разбиение множества R на смежные классы по аддитивной подгруппе J, называемые классами вычетов кольца R по модулю идеала J. Класс вычетов кольца R по модулю J, содержащий элемент aR обозначают через [a]=a+J, т.к. он состоит из всех элементов R вида a+c, где cJ. Элементы a,bR, принадлежащие одному и тому же классу вычетов по модулю J (т.е. такие, что a -bJ), называют сравнимыми по модулю J и обозначают ab(mod J). Для них справедливо: Если ab(mod J), то a+rb+r(mod J), arbr(mod J) rarb(mod J), nanb(mod J) nZ, rR. Если кроме того rs mod J), то a+rb+s(mod J) и arbs(mod J). Множество классов вычетов кольца R по модулю идеала J образует кольцо относительно операций + и . Эти операции определяются равенствами: (a+J)+(b+J)=(a+b)+J(1) (a+J)(b+J)=ab+J(2) Определение. Кольцо классов вычетов кольца R по модулю идеала J относительно операций (1), (2) называется факторкольцом кольца R по идеалу J и обозначается R/J. Пример. Факторкольцо (или кольцо вычетов) Z/(n). Как и в случае, когда мы рассматривали группы, обозначим класс вычетов по модулю n (nN) содержащий число aZ через [a]. Этот класс может быть записан в виде a+(n), где (n) идеал, порожденный числом n. Тогда элементами факторкольца Z/(n) будут [0]=0+(n), [1]=1+(n), ... , [n -1]=n -1+(n). Теорема. Факторкольцо Z/(p) кольца Z целых чисел по главному идеалу, порожденному простым числом Р, является полем. Идеал J кольца R называется главным, если существует элемент aR, такой что J=(a). Здесь, для коммутативного кольца R, величина (a)={ra+narR, nZ} - наименьший идеал, содержащий данный элемент aR. Если кольцо имеет единицу, то (a) ={rarR} ((a) - главный идеал). Пример. Пусть p=3 простое число. Тогда факторкольцо состоит из трех элементов [0],[1],[2]. Операции в этом кольце можно задать таблицами, аналогичными таблицам Кэли конечных групп
Приведенный пример является первым рассматриваемым нами образцом конечного поля, т.е. поля, содержащего конечное число элементов, которые играют основную роль в современной криптографии. |
