Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
7. Элементы теории конечного поля. Многочлены над конечными полями. Определение. Многочлен 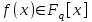 степени степени 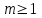 называется примитивным многочленом над полем называется примитивным многочленом над полем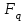 , если он является минимальным многочленом над , если он является минимальным многочленом над 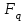 некоторого примитивного элемента расширения некоторого примитивного элемента расширения 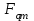 поля поля 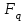 . .Это определение опирается на приведенные, на прошлой лекции понятия примитивного элемента и означает, что примитивный многочлен над 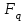 степени m - это нормированный многочлен который неприводим над степени m - это нормированный многочлен который неприводим над 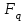 и имеет корень и имеет корень 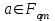 , который является образующим мультипликативной группы , который является образующим мультипликативной группы 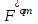 поля поля 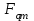 . .Теорема. Многочлен 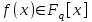 степени m является примитивным тогда и только тогда, когда он нормирован и, такой, что степени m является примитивным тогда и только тогда, когда он нормирован и, такой, что 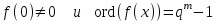 . .Рассмотрим теперь вопрос о числе нормированных неприводимых многочленов над конечным полем 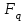 . .Теорема. Для каждого конечного поля 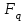 и каждого n произведение всех нормированных неприводимых многочленов над и каждого n произведение всех нормированных неприводимых многочленов над 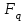 , степень которых делит n, равно , степень которых делит n, равно 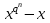 . .Следствие: Если 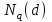 число нормированных неприводимых многочленов из число нормированных неприводимых многочленов из 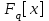 степени d, то степени d, то 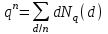 для всех n, где суммирование берется по всем положительным делителем d числа n. для всех n, где суммирование берется по всем положительным делителем d числа n.Из последнего выражения, используя арифметическую функцию Мебиуса можно получить точную формуле для числа нормированных неприводимых многочленов фиксированной степени из кольца 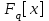 . .Для nN функция Мебиуса (n) удовлетворяет соотношению 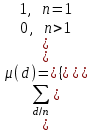 . .Тогда существует теорема: Число 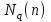 нормированных неприводимых многочленов степени n в кольце нормированных неприводимых многочленов степени n в кольце 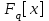 равно равно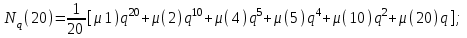 Для функции Мебиуса справедливо выражение 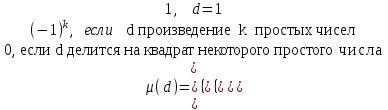 Тогда 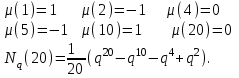  Перейдем к рассмотрению вопросов построения неприводимых многочленов. Ранее мы определили число нормированных многочленов данной степени n в кольце  . Получим теперь формулу для произведения всех нормированных неприводимых многочленов данной степени n из кольца . Получим теперь формулу для произведения всех нормированных неприводимых многочленов данной степени n из кольца 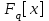 . .Теорема (*). Пусть 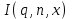 произведение всех нормированных неприводимых многочленов степени n из кольца произведение всех нормированных неприводимых многочленов степени n из кольца 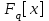 . Тогда оно определяется формулой . Тогда оно определяется формулой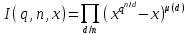 Пример: q=2, n=4. Здесь d=1,2,4. 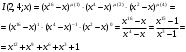 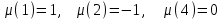 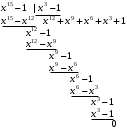 Все нормированные неприводимые многочлены степени n из 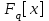 можно найти, различая на множители многочлен можно найти, различая на множители многочлен 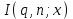 . В этой связи было бы полезно представить . В этой связи было бы полезно представить 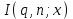 в частично разложенном виде. Этого можно добиться, опираясь на следующие факты. в частично разложенном виде. Этого можно добиться, опираясь на следующие факты.Теорема. Для поля F характеристики p и натурального числа n, не делящегося на р, n - круговой многочлен 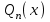 над F задается выражением: над F задается выражением: 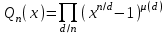 (1) (1)Отсюда имеет место теорема. Теорема. Пусть 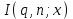 тоже, что и в теореме (*). Тогда для натурального числа n>1 имеет место формула тоже, что и в теореме (*). Тогда для натурального числа n>1 имеет место формула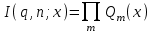 ,(2) ,(2)где 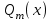 -m - круговой многочлен над -m - круговой многочлен над 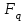 и произведение П берется по всем натуральным делителям m числа и произведение П берется по всем натуральным делителям m числа 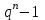 , для которых n является показателем, которому принадлежит число q по модулю m. (т.е. n -это наименьшее натуральное число, для которого , для которых n является показателем, которому принадлежит число q по модулю m. (т.е. n -это наименьшее натуральное число, для которого 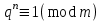 ) )Пример: Найдем все нормированные неприводимые многочлены степени n=4 из кольца 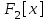 . Из равенства (2) следует . Из равенства (2) следует 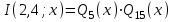 т.к. натуральными делителями m числа 24 -1=15, для которых n является показателем, которому принадлежит число q по модулю m т.е. т.к. натуральными делителями m числа 24 -1=15, для которых n является показателем, которому принадлежит число q по модулю m т.е. 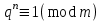 являются m=5 и m=15 . являются m=5 и m=15 .(Наименьшее натуральное число k такое, что 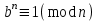 называется показателем, которому принадлежит число b по модулю n). называется показателем, которому принадлежит число b по модулю n). Натуральные делители числа 24 -1=15 это m=1,3,5,15. Для M=3 число n=4 не является показателем, которому принадлежит q=2 по модулю m=3, т.к. n=4 это не наименьшее натуральное число для которого, 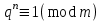 т.е. т.е. 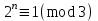 . Очевидно, при n=2 имеем . Очевидно, при n=2 имеем 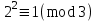 , поэтому делитель M=3 исключается из рассмотрения. , поэтому делитель M=3 исключается из рассмотрения.(если m=1, то n=4 также не является показателем, которому m число 2 по модулю 1 при n=1 это показатель). Определим теперь Q5(x) и Q15(x) из выражения (1): 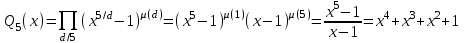 т.к. (1)=1 (5)= -1 и этот многочлен не приводим в F2[x], что следует из таблиц неприводимых многочленов. 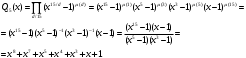 Q15 (x) разлагается в произведение двух неприводимых многочленов из F2 [x] степени 4. 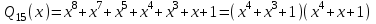 Таким образом, неприводимыми многочленами степени 4 из F2[x] являются три найденных многочлена, и только они. Перейдем теперь к рассмотрению другого важного вопроса, касающегося многочленов над конечными полями, а именно, к разложению многочленов над заданным полем в виде произведения неприводимых многочленов. Любой непостоянный многочлен над заданным полем можно разложить на произведение неприводимых многочленов. Если конечное поле малого размера. То имеется много эффективных алгоритмов для решения этой задачи. Для полей больших размеров также существуют соответствующие алгоритмы. Наличие таких алгоритмов особенно важно для решения прикладных проблем теории кодирования и криптографии. Чтобы понять специфику и оценить сложность данной задачи рассмотрим некоторые из указанных алгоритмов и лежащие в их основе теоретические результаты из теории конечных полей. Для любого многочлена 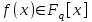 положительной степени существует каноническое разложение в кольце положительной степени существует каноническое разложение в кольце 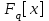 . При построении алгоритмов такого разложения достаточно ограничиться рассмотрением только нормированных многочленов. Таким образом, нашей целью является представление нормированного многочлена . При построении алгоритмов такого разложения достаточно ограничиться рассмотрением только нормированных многочленов. Таким образом, нашей целью является представление нормированного многочлена 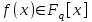 положительной степени в виде произведения положительной степени в виде произведения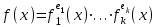 , ,где 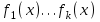 - различные нормированные неприводимые делители многочлена - различные нормированные неприводимые делители многочлена  в кольце в кольце 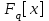 ; ;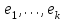 - натуральные числа. - натуральные числа.Прежде всего, упростим задачу, показав, что указанную проблему можно свести к проблеме разложения многочлена без кратных неприводимых сомножителей, т.е. когда все 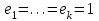 . .Для этого, применяя алгоритм Евклида, найдем многочлен, 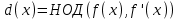 т.е. наибольший общий делитель т.е. наибольший общий делитель  и его производной и его производной 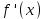 . .Если d(x)=1, то известно, что  не имеет кратных сомножителей (существует соответствующая теорема, доказывающая этот факт). не имеет кратных сомножителей (существует соответствующая теорема, доказывающая этот факт).Если 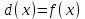 , то очевидно (т.к. , то очевидно (т.к. 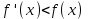 ) )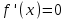 , а это значит, что , а это значит, что 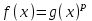 для некоторого многочлена для некоторого многочлена 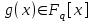 , где р - характеристика поля , где р - характеристика поля 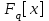 . Указанную процедуру редукции можно при необходимости повторить и для g(x) пока не получим представление . Указанную процедуру редукции можно при необходимости повторить и для g(x) пока не получим представление 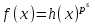 , где , где 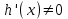 . .Если d(x) отличен от 1 и от  он является нетривиальным делителем он является нетривиальным делителем  и тогда многочлен и тогда многочлен 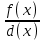 не имеет кратных неприводимых сомножителей. Мы придем к разложению не имеет кратных неприводимых сомножителей. Мы придем к разложению  , разложив по отдельности многочлены меньшей степени d(x) и , разложив по отдельности многочлены меньшей степени d(x) и 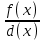 . Если d(x) все еще имеет кратные сомножители, для него повторяем указанный процесс редукции. . Если d(x) все еще имеет кратные сомножители, для него повторяем указанный процесс редукции.Таким образом, применяя описанную процедуру, нужное число раз, мы сведем исходную задачу к задаче разложения некоторого числа многочленов, не имеющих кратных неприводимых сомножителей. Канонические разложения этих многочленов сразу приведут к каноническому разложению исходного многочлена  . Это позволяет в дальнейшем рассматривать только многочлены, не имеющие кратных неприводимых сомножителей. В этом смысле следующая теорема является основной. . Это позволяет в дальнейшем рассматривать только многочлены, не имеющие кратных неприводимых сомножителей. В этом смысле следующая теорема является основной.Теорема. Если 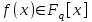 нормированный многочлен положительной степени и многочлен нормированный многочлен положительной степени и многочлен 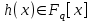 удовлетворяет условию удовлетворяет условию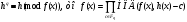 Представление в теореме выражения, вообще говоря, еще не дает полного разложения многочлена  , т.к. многочлен , т.к. многочлен 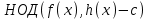 может оказаться приводимым в кольце может оказаться приводимым в кольце 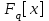 . Поэтому если h(x) таков, что указанная теорема приводит к некоторому нетривиальному разложению (но не полному) многочлена . Поэтому если h(x) таков, что указанная теорема приводит к некоторому нетривиальному разложению (но не полному) многочлена  , он называется , он называется 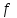 - разлагающим многочленом. Любой многочлен - разлагающим многочленом. Любой многочлен 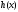 , обладающий свойством , обладающий свойством 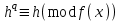 , очевидно, является , очевидно, является 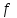 - разлагающим. Поэтому , чтобы на основе указанной теоремы добиться полного разложения - разлагающим. Поэтому , чтобы на основе указанной теоремы добиться полного разложения  мы должны найти способы построения мы должны найти способы построения 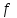 - разлагающих многочленов. Иными словами, задача разложения - разлагающих многочленов. Иными словами, задача разложения 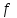 усложняется. Более того, даже если найдем способ построения усложняется. Более того, даже если найдем способ построения 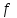 разлагающих многочленов из выражения для разлагающих многочленов из выражения для  в теореме видно, что для разложения в теореме видно, что для разложения  требуется вычисление q НОД, что при больших размерах полей (т.е.q) уже представляет собой вычислительную процедуру. требуется вычисление q НОД, что при больших размерах полей (т.е.q) уже представляет собой вычислительную процедуру.Тем не менее, рассмотрим один из способов построения 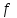 - разлагающих многочленов. Этот способ получил название алгоритма Берлекэмпа. В его основе лежит так называемая китайская теорема об остатках для многочленов: Пусть - разлагающих многочленов. Этот способ получил название алгоритма Берлекэмпа. В его основе лежит так называемая китайская теорема об остатках для многочленов: Пусть 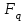 поле, и поле, и 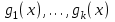 произвольные, а произвольные, а 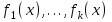 ненулевые попарно взаимно простые многочлены из ненулевые попарно взаимно простые многочлены из 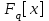 . Тогда система сравнений вида . Тогда система сравнений вида 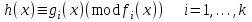 имеет единственное решение имеет единственное решение 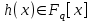 по модулю по модулю 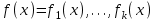 . .Допустим теперь, что  не имеет кратных сомножителей, так что не имеет кратных сомножителей, так что 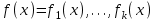 произведение различных нормированных неприводимых многочленов над полем произведение различных нормированных неприводимых многочленов над полем 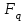 . Тогда для любого k -го набора . Тогда для любого k -го набора 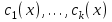 элементов поля элементов поля 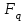 , согласно китайской теореме, существует единственный многочлен , согласно китайской теореме, существует единственный многочлен 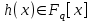 , такой что выполняется , такой что выполняется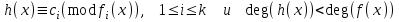 . .Этот многочлен удовлетворяет условию 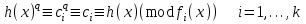 . .И поэтому справедливо сравнение: 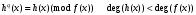 С другой стороны, если многочлен 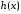 является решением сравнения, то из равенства является решением сравнения, то из равенства 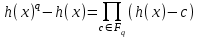 , в силу взаимной попарной простоты сомножителей правой части, следует, что каждый неприводимый делитель многочлена , в силу взаимной попарной простоты сомножителей правой части, следует, что каждый неприводимый делитель многочлена  должен делить один и только один из многочленов должен делить один и только один из многочленов 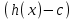 . Таким образом каждое решение . Таким образом каждое решение 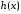 сравнения (1) удовлетворяет системе сравнений сравнения (1) удовлетворяет системе сравнений 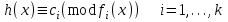 для некоторого k -го набора для некоторого k -го набора 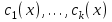 элементов поля элементов поля 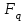 . Следовательно, данное сравнение имеет ровно . Следовательно, данное сравнение имеет ровно 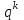 решений. решений.Чтобы найти эти решения сведем рассматриваемое сравнение к системе линейных уравнений. Полагая 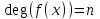 вычисляя вычисляя 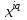 по модулю по модулю  посмотрим посмотрим 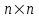 матрицу матрицу 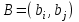 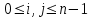 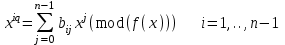 Тогда многочлен 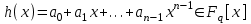 будет решением рассматриваемого сравнения тогда и только тогда, когда ( будет решением рассматриваемого сравнения тогда и только тогда, когда (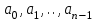 ) является решением системы линейных уравнений, которая в матричной форме имеет вид ) является решением системы линейных уравнений, которая в матричной форме имеет вид 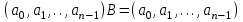 . Эту систему можно также записать в виде . Эту систему можно также записать в виде 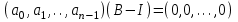 , где I единичная матрица , где I единичная матрица  на на  . Согласно доказанному выше, система уравнений имеет . Согласно доказанному выше, система уравнений имеет 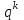 решений. Это значит, что размерность пространства решений этой системы равна K т.е. числу различных нормированных неприводимых делителей многочлена решений. Это значит, что размерность пространства решений этой системы равна K т.е. числу различных нормированных неприводимых делителей многочлена  , а ранг матрицы B -I равен r=n -k. Определяя ранг (здесь не будем описывать алгоритмы поиска ранга матриц т.к. их можно найти в известной литературе) r=n -k мы тем самым находим число K различных нормированных неприводимых делителей , а ранг матрицы B -I равен r=n -k. Определяя ранг (здесь не будем описывать алгоритмы поиска ранга матриц т.к. их можно найти в известной литературе) r=n -k мы тем самым находим число K различных нормированных неприводимых делителей  и тем самым можем узнать до каких пор необходимо продолжать процедуру разложения. Вычислив ранг u матрицы B -I находим число k=n -r. Если и тем самым можем узнать до каких пор необходимо продолжать процедуру разложения. Вычислив ранг u матрицы B -I находим число k=n -r. Если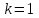 , значит , значит  неприводим над неприводим над 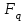 и процедура разложения заканчивается. Если и процедура разложения заканчивается. Если 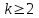 , то берем , то берем 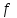 - разлагающий базисный многочлен - разлагающий базисный многочлен 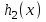 и находим и находим 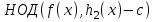 для всех для всех 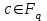 . В результате поучим некоторое нетривиальное разложение . В результате поучим некоторое нетривиальное разложение  . Если использование . Если использование 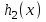 не привело к разложению не привело к разложению  на K сомножителей, то переходим к следующему на K сомножителей, то переходим к следующему 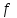 - разлагающему многочлену - разлагающему многочлену 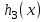 и находим и находим 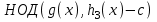 для всех для всех 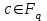 и всех нетривиальных делителей g(x) многочлена и всех нетривиальных делителей g(x) многочлена  , полученных на предыдущем этапе. Так продолжается до тех пор, пока не получим все K неприводимых сомножителей , полученных на предыдущем этапе. Так продолжается до тех пор, пока не получим все K неприводимых сомножителей  . Существует доказательство, что данный алгоритм сходится и позволяет привести к нахождению всех K сомножителей . Существует доказательство, что данный алгоритм сходится и позволяет привести к нахождению всех K сомножителей  . .Таким образом, в данном алгоритме задача вычисления 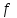 - разлагающих многочленов сводится к решению систем линейных уравнений, путем их представления в матричной форме записи. - разлагающих многочленов сводится к решению систем линейных уравнений, путем их представления в матричной форме записи.Из представленного алгоритма видно, насколько трудоемкой является процедура разложения произвольных многочленов над конечными полями заданной степени на произведение неприводимых многочленов. Этот факт и нашел широкое применение таких трудоемких задач при построении различных криптографических систем. С понятием многочленов и процедурами их деления друг а друга тесно связаны вопросы формирования линейных рекуррентных последовательностей над конечными полями, которые находят широкое применение при создании поточных криптосистем. Поэтому рассмотрим вопросы формирования линейных рекуррентных последовательностей над конечными полями. |
