Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
последовательностей. Схема открытого распределения ключей Диффи и Хеллмана. Подавляющее большинство современных криптографических систем используют либо поточные, либо блочные алгоритмы, базирующиеся на различных типах шифрах замены и перестановки. К сожалению, практически все алгоритмы, используемые в поточных криптосистемах, ориентированных на использование в военных и правительственных системах связи, а также, в некоторых случаях, для защиты информации коммерческого характера, что вполне естественно делает их секретными и недоступными для ознакомления. Единственными стандартными алгоритмами поточного шифрования являются уже упоминавшийся на прошлой лекции американский стандарт DES (режимы CFB и OFB) и российский стандарт ГОСТ 28147-89 (режим гаммирования). При этом алгоритмы поточного шифрования, используемые в этих стандартах, являются засекреченными. Основу функционирования поточных криптосистем составляют генераторы случайных или псевдослучайных последовательностей. Рассмотрим этот вопрос более подробно. Псевдослучайные последовательности чисел для поточных криптосистем. Секретные ключи представляют собой основу криптографических преобразований, для которых согласно правилу Керкхоффа, стойкость криптосистемы определяется лишь секретностью ключа. Основной проблемой классической криптографии долгое время являлась трудность генерации секретного ключа. Физическое моделирование случайности с помощью таких физических явлений как, например, радиоактивное излучение или дробовой шум в электронной лампе является довольно сложным и дорогостоящим и к тому же не дают полностью настоящих случайных процессов. Поэтому вместо физического моделирования используют методы математического моделирования случайности и генерации случайных последовательностей в виде программ для ЭВМ или специализированных устройств. Эти программы и устройства хотя и называются генераторами случайных чисел, на самом деле генерируют детерминированные последовательности, которые только кажутся случайными по своим свойствам и поэтому называются псевдослучайными последовательностями. От них требуется, чтобы, даже зная закон формирования, но не зная ключа в виде заданных начальных условий, никто не смог бы отличить генерируемую последовательность от случайной, как будто она получена путем бросания идеальных игровых костей. Можно сформировать три основных требования, которым должны удовлетворять криптографически стойкие генераторы псевдослучайных последовательностей или гаммы. 1. Период гаммы должен быть достаточно большим для шифрования сообщений различной длины. 2. Гамма должна быть трудно предсказуемой. Это значит, что если известны тип генератора и кусок гаммы, то невозможно предсказать следующий за этим куском бит гаммы или предшествующий этому куску бит гаммы. 3. Генерирование гаммы не должно быть связано с большими техническими и организационными трудностями. Самая важная характеристика генератора псевдослучайных чисел - это информационная длина его периода, после которого числа будут либо просто повторяться, либо их можно будет предсказать. Эта длина практически определяет возможное число ключей криптосистемы. Чем эта длина больше, тем сложнее подобрать ключ. Второе из указанных выше требований связано со следующей проблемой: на основании чего можно сделать заключение, что гамма конкретного генератора действительно является непредсказуемой? Пока в мире нет универсальных и практически проверяемых критериев для проверки этого свойства. Интуитивно случайность воспринимается как непредсказуемость. Чтобы гамма считалась случайной и непредсказуемой как минимум необходимо, чтобы ее период был очень большим, а различные комбинации бит определенной длины равномерно распределялись по всей ее длине. Это требование статистически можно толковать и как сложность закона генерации псевдослучайной последовательности чисел. Если по достаточно длинному отрезку этой последовательности нельзя ни статистически, ни аналитически определить этот закон генерации, то в принципе этим можно удовлетвориться. И, наконец, третье требование должно гарантировать возможность практической реализации генераторов псевдослучайных последовательностей с учетом требуемого быстродействия и удобства практичного использования. Рассмотрим теперь некоторые практические методы получения псевдослучайных чисел. Одним из первых таких методов был метод, предложенный в 1946 году Д. фон Нейманом. Этот метод базировался на том, что каждое последующее число в псевдослучайной последовательности формировалось возведением предыдущего числа в квадрат и отбрасыванием цифр с обоих концов. Однако этот метод оказался ненадежным, и от него быстро отказались. Другим методом является так называемый конгруэнтный способ. Его математическое выражение имеет вид:  Здесь каждое последующее случайное число  получается умножением предыдущего числа получается умножением предыдущего числа 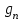 на k сложением с c и взятием остатка от деления на m. Главной проблемой здесь было подобрать хорошие значения коэффициентов k, c, m. Выбор в качестве k, c, m иррациональных чисел, требующих для своего представления бесконечного числа знаков, практически не реализуем. Выбор почти иррациональных чисел представленных, например, 4 байтами в формате с плавающей запятой, дает псевдослучайные последовательности с периодами всего лишь 1225 и 147 в зависимости от начального заполнения. Исследования показали, что более эффективно вести вычисления в целых числах. Для них, в частности, было показано, что при c = 0, на k сложением с c и взятием остатка от деления на m. Главной проблемой здесь было подобрать хорошие значения коэффициентов k, c, m. Выбор в качестве k, c, m иррациональных чисел, требующих для своего представления бесконечного числа знаков, практически не реализуем. Выбор почти иррациональных чисел представленных, например, 4 байтами в формате с плавающей запятой, дает псевдослучайные последовательности с периодами всего лишь 1225 и 147 в зависимости от начального заполнения. Исследования показали, что более эффективно вести вычисления в целых числах. Для них, в частности, было показано, что при c = 0,  наибольшей период составит m/4 при k = 3+8j или k= 5+8j и нечетном начальном числе. При этом при достаточно больших к последовательность производит впечатление случайной. Дальнейшие исследования показали, что если c нечетно, а k= 1+4, то период можно увеличить до числа наибольшей период составит m/4 при k = 3+8j или k= 5+8j и нечетном начальном числе. При этом при достаточно больших к последовательность производит впечатление случайной. Дальнейшие исследования показали, что если c нечетно, а k= 1+4, то период можно увеличить до числа  . После долгих поисков числа k исследователи остановились на значениях k = 69069 и k= 71365. . После долгих поисков числа k исследователи остановились на значениях k = 69069 и k= 71365.Интересный класс генераторов псевдослучайных последовательностей основан на использовании последовательностей Фибоначчи. Классический пример такой последовательности {0,1,1,2,3,5,8,13,21,34 …} - за исключением первых двух ее членов, каждый последующий член равен сумме двух предыдущих. Если брать только последнюю получающуюся в результате суммирования цифру, то получим {0,1,1,2,3,5,8,3,1,4 …} Если ввести в схему Фибоначчи «бит переноса», который может иметь начальные значения 0 или 1, то можно построить генератор сложения с переносом, который по своим свойствам превосходит конгруэнтные генераторы. И, наконец, построение псевдослучайных последовательностей с гарантированно хорошими для криптографии свойствами (максимальная длина периода, равномерный спектр) возможно путем использования аппарата и результатов теории линейных рекуррентных последовательностей над конечными полями, о которых мы подробно говорили на прошлых лекциях. Получаемые при помощи рассмотренных методов псевдослучайные последовательности, используются в поточных криптосистемах для игнорирования сообщений путем использования различных типов шифров замены. Например, для шифрования сообщений может быть использована та или иная модификация известной уже вам системы Вернама: 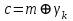 , где , где 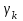 - псевдослучайная последовательность чисел, определяемая секретным ключом k. - псевдослучайная последовательность чисел, определяемая секретным ключом k.Примерами стандартизованных алгоритмов блочных криптосистем являются американский стандарт DES (режим электронной кодовой книги ЕСВ) и российский стандарт ГОСТ 28147-89 (режим простой замены). Поскольку описание этих алгоритмов носит закрытый характер, проиллюстрируем работу блочных алгоритмов на примере описания работы криптосистем с открытым ключом, в частности, системы на базе алгоритма RSA. Схема открытого распределения ключей Диффи и Хеллмана. Прежде чем перейти к описанию алгоритма функционирования RSA криптосистемы с открытым ключом рассмотрим, лежащий в ее основе, принцип работы схемы открытого распределения ключей, предложенной в 1976 году Диффи и Хеллманом. Схема открытого распределения ключей предполагает, что все пользователи знают некоторое простое число Р и примитивный элемент a (1<a<P) конечного поля Галуа GF(p) (примитивный элемент, а это такой элемент степени 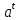 которого дают все элементы поля GF(p)). Такие элементы всегда существуют и их число равно которого дают все элементы поля GF(p)). Такие элементы всегда существуют и их число равно 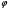 ( (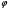 (p)), где (p)), где 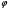 - функции Эймера. Для выработки общей секретной информации К пользователи А и В должны сделать следующее: - функции Эймера. Для выработки общей секретной информации К пользователи А и В должны сделать следующее:1. Пользователи А и В независимо выбирают случайные числа Ka и Kb из интервала (1,…,р -1), называемые секретными ключами пользователей. 2. Пользователи А и В на основе известных параметров a и рвычисляют величины: yA= aKA(modp); YB= aKB(modp), которые являются открытыми ключами пользователей. 3. Пользователи АиВобмениваются этими ключами по открытому каналу связи (с подтверждением авторства, чтобы избежать замены их кем - то другим, т.е. с использованием процедуры аутентификации). 4. По полученным значениям yA и yBкаждый из пользователей независимо вычисляет секретный параметр К, который и будет их общим сеансовым секретным ключом: A: K=yBKA (mod p)=[aKB]KA(mod p)=aKBKA (mod p) B: K=yAKB (mod p)=[aKA]KB(mod p)=aKAKB (mod p). Стойкость такой системы зависит от сложности вычисления дискретных логарифмов в мультипликативной группе конечного поля в F(p). Эта стойкость гарантирована тем, что до настоящего времени не найдено быстрых алгоритмов нахождения аКАКВ иза, аКА, аКВбез вычисленияКА из а, аКАили КВ из а, аКВ. Описанная схема открытого распределения ключей совместно с введенным понятием односторонней функции с секретом послужили основой для создания принципа открывать составившего новое направление в области построения криптографических систем. Такие системы получили название криптосистем с открытым ключом. Основная идея принципа открытого шифрования заключается в следующем: если получатель секретного сообщения выберет одностороннюю функцию с секретом fK(x) и сообщит по открытому каналу отправителю эффективный алгоритм ЕК ее вычисления, то тот может вычислить значение функции fK(M)=Cот сообщения Ми передать это значение по открытому каналу получателю. Только тот, кто знает (в данном случае получатель) секретный ключ К, знает и алгоритм DK вычисления обратной функции fK-1(c)и может определить исходный текстM=fK -1(c). В общем виде криптографическая система с открытым ключом представляет собой систему, включающую следующие компоненты: - пространство открытых текстов  ; ;- пространство шифротекстов 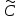 ; ;- пространство секретных ключей 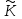 ; ;- множество преобразований зашифрования ЕК, 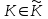 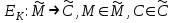 ; ;- множество преобразований расшифрования 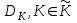  При этом преобразования ЕКиDKдолжны обладать следующими свойствами: 1. Для каждого 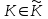 преобразование преобразование 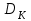 является обратным к преобразованию ЕК т.е. является обратным к преобразованию ЕК т.е. 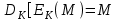 при всех при всех 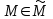 . .2. По каждому выбранному ключу 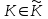 легко найти пару обратимых преобразований ЕК иDK.. легко найти пару обратимых преобразований ЕК иDK..3. Для всех 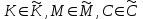 величины EK(M) иDK(C) легко вычисляются за полиномиальное время. величины EK(M) иDK(C) легко вычисляются за полиномиальное время.4. Почти для всех 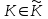 вычислительно невозможно из ЕК вывести какое - либо легко вычисляемое преобразование, эквивалентное DK . вычислительно невозможно из ЕК вывести какое - либо легко вычисляемое преобразование, эквивалентное DK .Свойство 4 отличает криптосистемы с открытым ключом от традиционных криптосистем с секретным ключом, в которых преобразования EKи DKтакже зависят от секретного ключа К, но знание преобразования ЕКдает знание КиDKили наоборот, знание DKпозволяет определить К иЕК , поэтому преобразования EKи DKлибо оба известны, либо оба неизвестны. Это свойство 4 позволяет не засекречивать преобразование зашифрования ЕК, а делать его открытым для всех, кто хочет послать секретное сообщение. Так как в силу открытости любой злоумышленник имеет доступ к преобразованию зашифрования ЕК, то он может всегда выбрать любой открытый текст и получить соответствующий ему шифрованный текст. Поэтому системы с открытым ключом должны быть всегда устойчивы к методам атаки по выбранному открытому тексту. Криптосистемы с открытым ключом обеспечивают только практическую стойкость. 12. Алгоритм RSA и алгоритм Эль Гамаля работы криптосистем с открытым ключом. Цифровая подпись. Алгоритм цифровой подписи Эль Гамаля. Алгоритм Ривеста (Rivest) - Шамира (Shamir) – Алдемана (Aldeman) – RSA(1978 год). Одной из первых криптосистем с открытым ключом была предложенная в 1978 году система на алгоритма RSA. Как видно название алгоритма, RSA образовано из первых букв фамилий авторов этого алгоритма. В его основе лежит использование степенной односторонней функции с секретом, которую мы рассматривали на прошлых лекциях. RSA относится к блочным алгоритмам, так как каждый блок 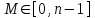 открытого текста, представленный как целое число из интервала (1,2,…,n -1), преобразуются в блок открытого текста, представленный как целое число из интервала (1,2,…,n -1), преобразуются в блок 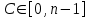 шифрованного текста путем вычисления шифрованного текста путем вычисления 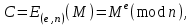 где e, n– ключ преобразования зашифрования. При расшифровании блок отрытого текста Мвосстанавливается также путем экспоненцирования, но с другой степенью dв качестве ключа расшифрования, т.е. 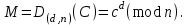 Зашифрование и расшифрование могут быть выполнены с использованием быстрых алгоритмов экспоненцирования не более чем за 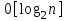 операций. операций.В основе алгоритма лежит известная уже теорема Эйлера, согласно которой для каждого целого числа М, взаимно простого с модулем n(т.е. MOD(M, n)=1) выполняется соотношение  где 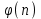 - функция Эйлера, т.е. число целых чисел < nи взаимно простых сn. - функция Эйлера, т.е. число целых чисел < nи взаимно простых сn.Можно показать, что если числа eиd удовлетворяют соотношению  а 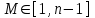 взаимно просто с n, то взаимно просто с n, то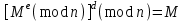 , ,что в свою очередь означает, что 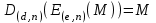 . .Действительно, 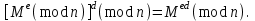 Условие 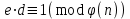 означает, что 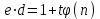 для некоторого целого t. Тогда 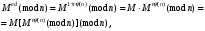 где 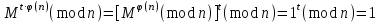 . .Значит 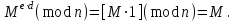 При наличии 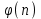 можно легко найти пару чисел е и d, удовлетворяющих соотношению можно легко найти пару чисел е и d, удовлетворяющих соотношению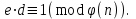 Для этого выбирается число е взаимно простое с 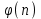 , что можно проверить с помощью алгоритма Евклида. Взаимная простота нужна для разрешимости сравнения , что можно проверить с помощью алгоритма Евклида. Взаимная простота нужна для разрешимости сравнения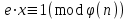 относительно неизвестного х. Число х=d определяется с помощью алгоритма Евклида, определяющего числа d и t, удовлетворяющие соотношению  , что и означает справедливость сравнения , что и означает справедливость сравнения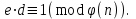 При этом, сложность алгоритма Евклида не превосходит 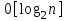 операций. операций.Все сказанное выше справедливо для произвольного целого модуля n. В алгоритме RSA модуль n есть произведение простых чисел pиq, т.е. n=p·q. Поэтому в данном случае 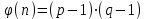 и любое простое число e>max(p,q) будет взаимно простым с и любое простое число e>max(p,q) будет взаимно простым с 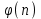 , т.е. при выборе ключа зашифрования е можно не применять алгоритм Евклида, а воспользоваться известными быстрыми тестами проверки числа е на простоту. , т.е. при выборе ключа зашифрования е можно не применять алгоритм Евклида, а воспользоваться известными быстрыми тестами проверки числа е на простоту.Без знания простых сомножителей pи q значение функции 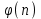 , а значит и ключей еи d определить очень трудно. Поэтому если делать открытыми числа eи n, а число d держать в секрете, то нахождение М из С сводится к трудной задаче извлечения корня степени е из числа С по модулю n. Это и означает, что алгоритм RSA может быть использован для построения криптосистемы с открытым ключом, т.е. системы открытого шифрования, когда преобразование зашифрования , а значит и ключей еи d определить очень трудно. Поэтому если делать открытыми числа eи n, а число d держать в секрете, то нахождение М из С сводится к трудной задаче извлечения корня степени е из числа С по модулю n. Это и означает, что алгоритм RSA может быть использован для построения криптосистемы с открытым ключом, т.е. системы открытого шифрования, когда преобразование зашифрования 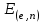 открыто, а преобразование расшифрования открыто, а преобразование расшифрования 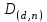 держится в секрете. держится в секрете.С учетом описанного выше алгоритма RSA работу криптосистемы с открытым ключом можно представить в виде следующей последовательности действий: 1. Пользователь выбирает два больших простых числа p и q и вычисляет два произведения 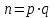 и и 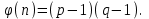 2. Затем пользователь выбирает случайное целое число е и вычисляет число d, удовлетворяющее условию 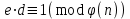 , ,т.е. 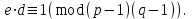 3. После этого пользователь публикует другим пользователям числа е и n как свой открытый ключ, сохраняя при этом найденное число d в секрете как закрытый ключ. 4. Если М сообщение, длина которого определяется по значению выражаемого им целого числа, должна быть в интервале от 1 до n, то оно преобразуется в шифровку с возвращением в степень ечисла М по модулю n и отправляется получателю (пользователю, который знает ключ d) 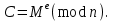 5. Получатель сообщения (пользователь , у которого хранится ключ d) расшифровывает сообщение С, возводя его в степень d по модулю n, т.е. 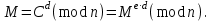 Пример. Пусть р=211, q=223 – простые числа. Тогда n=p·q=47053, 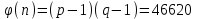 . Выберем открытый ключ с = 16813 и вычислим секретный ключ расшифрования dтакой, что . Выберем открытый ключ с = 16813 и вычислим секретный ключ расшифрования dтакой, что 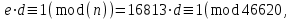 откуда d= 19837. Возьмем в качестве сообщения М название алгоритма, т.е. RSA. Чтобы перевести RSA в число будем считать букву R= 18, S= 19, A = 1 по порядковому номеру в латинском алфавите. На представление каждой буквы отведем по 5 бит числа, представляющего открытый текст М. Тогда слову RSA будет соответствовать число 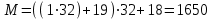 С помощью открытого ключа е получим шифровку: 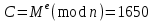 16813 16813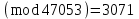 . .Получатель расшифрует эту шифровку с помощью секретного ключа d   . .Для полноты изложения отметим, что для алгоритма RSA существует малая вероятность того, что шифровка числа М возведем в степень е по модулю n может не изменить открытый текст М. Это следует из теоретического факта, что для каждого значения е существует, по крайней мере, 9 таких значений М, что 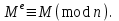 Например, для n=p·q= 47·59=2773 это числа М = 0,1,2773,2537,2303,235,2538,471,236. В алгоритме RSA вместо функции Эйлера 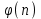 можно использовать функцию Кармайкла можно использовать функцию Кармайкла 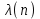 , которая для произвольного целого числа определяется , которая для произвольного целого числа определяется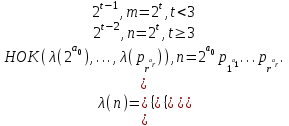 Для 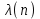 справедлива теорема Камайкла, обобщающая теорему Эйлера: для любого целого М, взаимно простого с числом n, верно сравнение справедлива теорема Камайкла, обобщающая теорему Эйлера: для любого целого М, взаимно простого с числом n, верно сравнение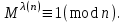 Если теперь в алгоритме RSA заменить 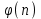 на на 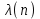 и при n=p·q считать и при n=p·q считать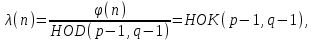 то получим модификацию RSA на основе функции Кармайкла 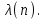 Стойкость алгоритма RSA можно оценить сверху сложностью разложения целого числа n на простые сомножители p и q с последующим определением 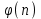 . Это весьма трудная задача. . Это весьма трудная задача. Другим примером криптосистемы с открытым ключом является система открытого шифрования Эль Гамаля, предложенная в 1985 году. Алгоритм, лежащий в основе этой системы, предлагает следующую последовательность действий: 1. Отправитель Аи получатель В знают большое простое число Р. Сообщения М представляются целыми числами из интервала {1, p} т.е. M=2,…, p -1. Отправитель А генерирует случайное число 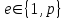 , получатель В также генерирует случайное число d из интервала {1, p}. , получатель В также генерирует случайное число d из интервала {1, p}. 2. Отправитель А шифрует сообщение ключом е в виде 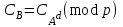 и посылает его В. и посылает его В.3. Получатель Вшифрует принятое сообщение 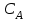 своим ключом d в виде своим ключом d в виде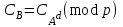 и посылает его А. 4. Отправитель А «снимает» свой ключ операцией  и возвращает С получателю В. 6. Получатель В расшифровывает сообщение 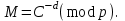 Стойкость этой криптосистемы с открытым ключом основана на том, что достаточно лично вычислить степень любого целого числа, умножив его на самого себя, требуемое число раз. В тоже время весьма трудно найти ключи е и d, т.е. показатель степени, в которую нужно возвести заданное число, чтобы получить другое заданное число. Это задача поиска дискретного логарифма некоторого числа а по модулю n, которая еще более сложна, чем разложение целого числа на простые сомножители. Следует отметить, что специалисты в области криптологии пока не очень доверяют алгоритмам открытого шифрования и предпочитают их использовать только для реализации процедур рассылки секретных ключей пользователям и аутентификации сообщений (подтверждения подлинности сообщения и лица пославшего сообщения), в то время как шифровку самых сообщений предпочитают осуществлять классическими криптографическими методами замены или перестановки. Поэтому одним из основных применений алгоритмов и систем открытого шифрования является в настоящее время их использования при создании так называемой цифровой подписи, позволяющей подтвердить подлинность получаемых пользователем сообщений. Рассмотрим принципы построения схемы цифровой подписи. Схема цифровой подписи. Существенным недостатком многих электронных систем передачи данных является отсутствие возможности проверки подлинности и авторства пересылаемых документов. Это не позволяет использовать такие системы для заключения юридически признаваемых сделок или для передачи юридически подтверждаемых документов, что часто сводит на нет преимущества таких систем по сравнению с обычной почтовой пересылкой. Как правило, в таких системах полученный документ распечатывается на бумажный носитель, подписывается физическим лицом и удостоверяется печатью юридического лица. Эту проблему можно решить путем использования электронной цифровой подписи, т.е. средства, позволяющего на основе криптографических методов надежно установить авторство и подлинность документа. Наиболее простой вид цифровой подписи представляет собой так называемый имитоприставка, которая реализуется в виде шифра контрольной суммы по сообщению. В качестве такой контрольной суммы по сообщению может использоваться какое - либо число, отпечаток пальца, и др. Однако в полной мере подлинность и авторство документа устанавливает электронная цифровая подпись, позволяющая заменить при безбумажном документообороте традиционные подпись и печать. Цифровая подпись зависит от текста заверяемого документа, секретного ключа, доступного только заверяющему лицу, и несекретного общедоступного ключа. Для реализации схемы цифровой подписи требуется, чтобы преобразования зашифрования ЕK и расшифрования DK также действовали на пространствах открытых текстов  и шифротекстов и шифротекстов 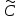 и преобразование ЕK было бы обратным преобразованием к DK, т.е.: и преобразование ЕK было бы обратным преобразованием к DK, т.е.:ЕK: 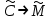 DK:  EK[DK(M)]=M для любого открытого текста 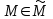 . .Если теперь некоторый пользователь А желает послать сообщение М пользователю В с подтверждением своего авторства, то он может воспользоваться своим секретным ключом, т.е. преобразованием DK=DK,A, вычислить величину C=DK,A[M] и послать это значение (это и будет цифровой подписью) пользователю В. в этом случае преобразование DK,A используется для шифрования текста М и цифровая подпись обратна алгоритму открытого шифрования. Пользователь В, также как и любой другой пользователь, знающий открытое преобразование EK,A может убедиться в авторстве сообщения М вычислением этого сообщения из соотношения 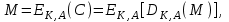 и проверкой, является ли М осмысленным текстом. Т.е. здесь EK,A действуют как преобразование расшифрования. Авторство пользователя А основано на том, что только он знает секретное преобразование DK,A . Злоумышленник, желающий подменить сообщение М на другое сообщение 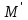 , должен решить задачу нахождения такого значения С, что , должен решить задачу нахождения такого значения С, что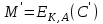 . .В силу односторонней природы (используется односторонняя функция) преобразования сделать это крайне трудно. Обычно на практике, для сокращения времени подписывания преобразования 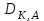 применяется не для всего исходного текста М, а для некоторой его хэш-функции H(M) , которая отображает любое сообщение М в сообщение H(M) фиксированного малого размера. Другими словами, цифровая подпись имеет вид применяется не для всего исходного текста М, а для некоторой его хэш-функции H(M) , которая отображает любое сообщение М в сообщение H(M) фиксированного малого размера. Другими словами, цифровая подпись имеет вид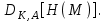 Пользователь В, получив сообщение Ми подпись к нему DK,A может вычислить (функция хэширования общеизвестна) и проверить выполнимость соотношения 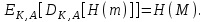 С учетом сказанного, общую схему цифровой подписи может представить следующим образом: схема включает: 1. Пространство открытых сообщений  к которым применяется алгоритм цифровой подписи. к которым применяется алгоритм цифровой подписи. 2. Пространство секретных параметров 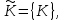 которые выбираются пользователем. которые выбираются пользователем.3. Алгоритм генерации за полиномиальное время пары (EK,DK) - открытого и секретного ключей по выбранному параметру К. 4. Алгоритм подписи Q, который вырабатывает значение Q [М, DK], называемое цифровой подписью сообщению М. 5. Алгоритм проверки подписи, который проверяет правильность подписи и сообщение с использованием открытого ключа ЕK. Рассмотрим теперь конкретный алгоритм цифровой подписи, предложенный Эль Гамалем (1985) Все пользователи знают большое простое число и примитивный элемент 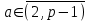 по модулю Р. Секретная информация подписывающего пользователя А состоит из двух частей: по модулю Р. Секретная информация подписывающего пользователя А состоит из двух частей:1. 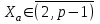 - долговременный секретный ключ подписи выбирается случайно из интервала - долговременный секретный ключ подписи выбирается случайно из интервала  и хранится в секрете. и хранится в секрете.2. 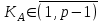 - разовый секретный ключ подписи конкретного сообщения, такой что - разовый секретный ключ подписи конкретного сообщения, такой что 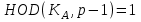 , т.е. , т.е. 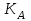 взаимно просто с p -1. взаимно просто с p -1.Открытая информация подписывающего тоже имеет 2 части: 1. 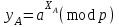 - открытый ключ подписи. - открытый ключ подписи.2. 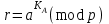 - первая из двух частей подписи (r,s). - первая из двух частей подписи (r,s).Подписываемое сообщение представляется числом из интервала (0,p -1) точнее его функцией хэширования H(M). АЛГОРИТМ ПОДПИСИ СООБЩЕНИЯ М: 1. Пользователь А выбирает случайное число из интервала 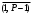 , таким образом, чтобы НОД , таким образом, чтобы НОД 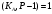 2. Вычисляет 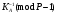 т.е. число удовлетворяющее сравнению т.е. число удовлетворяющее сравнению 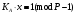 Именно для разрешимости этого сравнения при выборе Именно для разрешимости этого сравнения при выборе 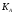 наложено условие его простоты, с наложено условие его простоты, с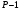 . .3. Вычисляем первую часть подписи 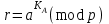 . .4. Вычисляем вторую часть подписи по формуле 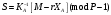 . .На этом процедура выработки подписи (r,S) к сообщению М заканчивается, и эти данные M,r,S сообщаются получателям. АЛГОРИТМ ПРОВЕРКИ ПОДПИСИ К СООБЩЕНИЮ М По полученным данным M, r, S и имеющемуся у получателя открытому ключу отправителя yA вычисляются величины  и и 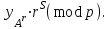 В случае выполнения равенства В случае выполнения равенства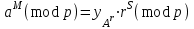 считается, что подпись верная. Поясним работу алгоритмов. Рассмотрим проверяемое равенство 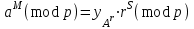 или сравнение или сравнение 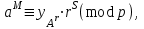 решением которого и является числа r и s. После подстановки yA и rоно примет вид решением которого и является числа r и s. После подстановки yA и rоно примет вид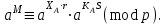 Учитывая свойства сравнений (теорема Эйлера - Ферма), последнее эквивалентно сравнение по модулю (Р – 1) вида: 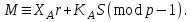 Именно из этого сравнения подписывающий пользователь вычисляет величину 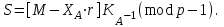 Особенностью алгоритмов цифровой подписи является наличие у подписывающего абонента секретного ключа 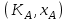 . При этом, в случае проверки, он предъявляет контролеру не сам секретный элемент, а некоторые значение функции, вычисляемое с помощью секретного ключа по случайному запросу контролера, доказывая тем самым, что он обладает секретом, путем его косвенной демонстрации, путем вычислений. Именно отсюда появилось название «доказательство при нулевом знании», которое получил протокол общения абонентов, когда абонент доказывает, что он обладает секретом, не раскрывая самого секрета. Алгоритмы «доказательства при нулевом знании» не являются собственно криптографическими, т.к. они служат для передачи сообщений типа « я знаю эту информацию». Однако, такие алгоритмы совместно с алгоритмами цифровой подписи, шифрования с открытым ключом и открытого распределения ключей позволяют организовывать более совершенные протоколы взаимодействия пользователей криптографической сети, которые реализуют одновременно и подтверждение подлинности документов и доказательство при нулевом знании. . При этом, в случае проверки, он предъявляет контролеру не сам секретный элемент, а некоторые значение функции, вычисляемое с помощью секретного ключа по случайному запросу контролера, доказывая тем самым, что он обладает секретом, путем его косвенной демонстрации, путем вычислений. Именно отсюда появилось название «доказательство при нулевом знании», которое получил протокол общения абонентов, когда абонент доказывает, что он обладает секретом, не раскрывая самого секрета. Алгоритмы «доказательства при нулевом знании» не являются собственно криптографическими, т.к. они служат для передачи сообщений типа « я знаю эту информацию». Однако, такие алгоритмы совместно с алгоритмами цифровой подписи, шифрования с открытым ключом и открытого распределения ключей позволяют организовывать более совершенные протоколы взаимодействия пользователей криптографической сети, которые реализуют одновременно и подтверждение подлинности документов и доказательство при нулевом знании.Общая идея алгоритмов доказательства при нулевом знании состоит в том, что он может вычислять некоторую функцию, зависящую от секретного ключа и от аргументов, задаваемых проверяющим. Проверяющий, даже зная эти аргументы, не может по данному ему значению функции восстановить секретный ключ. При этом функция должна быть такой, чтобы проверяющий мог удостовериться в правильности ее вычисления, например, эта функция может представлять собой цифровую подпись выбранных им аргументов. Рассмотрим алгоритм доказательства при нулевом знании, в основе которого лежит описанный ранее алгоритм RSA: 1. Доказывающий А и контролер В, оба знают идентификатор I и открытый ключ n, e, но А, кроме того, знает еще секретное число 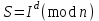 , сформированное по секретному ключу d. Сначала А генерирует случайное число Х и вычисляет , сформированное по секретному ключу d. Сначала А генерирует случайное число Х и вычисляет  . Затем он отсылает I,y к B. . Затем он отсылает I,y к B.2. После этого В генерирует и передает А случайное число V. 3. Затем Авычисляет и передает В число 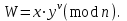 4. Контролер В проверяет принадлежность идентификатора I к А путем проверки тождества 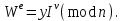 Список рекомендуемой литературы. Лидл Р.,Нидеррайтер Г. Конечные поля. М.: Мир, 1998. Том 1,2,822с. Варфоломеев А., Пеленицин М. Методы криптографии и их применение в банковских технологиях. Учебное пособие. М.: МИФИ, 1995-116с. Жельников В. Криптография от папируса до компьютера. М.: АBF, 1997-336с. Мельников В.В. Защита информации в компьютерных системах. М.: Финансы и статистика, 1997-425с. Герасименко В.А., Малюк А.А. Основы защиты информации. М.: МИФИ, 1997-537с. Фомичев В.М. Симметричные криптосистемы. Учебное пособие. М.: МИФИ, 1995-325с. Давыдова Е.В., Дмитриев И.Л., Курепкин И.А. Новые средства криптографической защиты информации. Учебное пособие. М.: МИФИ, 1996-132с. Галуев Геннадий Анатольевич МАТЕМАТИЧЕСКИЕ ОСНОВЫ КРИПТОЛОГИИ: Учебно-методическое пособие ПОКУРСУ МАТЕМАТИЧЕСКИЕ ОСНОВЫ КРИПТОЛОГИИ Для студентов специальностей 075300, 075400, 075600. всех форм обучения Ответственный за выпуск Галуев Г.А. ЛР №020565 от 23 июня 1997г. Подписано к печати 24.05.2003 г. Формат 60х80 1/16 Бумага офсетная. Офсетная печать. Усл. п. л. 8,2. Уч.- изд. л. 8,0 <<C>> Издательство Таганрогского государственного радиотехнического университета ГСП 17 А, Таганрог,28, Некрасовский, 44 Типография Таганрогского государственного радиотехнического университета ГСП 17 А, Таганрог,28, Энгельса, 1   |
