Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
10. Общая характеристика различных типов шифров и классов криптосистем. Ранее (на первой лекции) уже сообщалось об основных типах шифров (шифры замены и перестановки) и классах криптосистем (поточные, блочные), используемых в современной криптографии, рассмотрим более детально эти вопросы. Шифры замены. Шифры этого типа делятся на две группы: шифры простой замены и шифры сложной или многоалфавитной замены, например, система Виженера, шифр Гронсфельза. В настоящее время для шифрования используют ЭВМ, где каждый знак исходного текста представлен двоичным кодом заданной длины. Самый простой и эффективный шифр замены в этом случае - это модификация шифра Вернама т.е. когда исходное сообщение в виде последовательности бит смешивается при помощи операции XOR (сложение по модулю 2) со случайной двоичной последовательностью чисел, заданной выбранным секретным ключом. В этом случае информация, содержащаяся в исходном сообщении, прячется в шуме, т.е. самом информативном по определению К. Шеннона сигнале. (Песчинку лучше прятать на пляже, рыбу в море среди других таких же рыб, а информацию в шуме). Специфика этого шифра состоит в том, что процедура шифрования совпадает с процедурой расшифрования. Если последовательность бит исходного сообщения - m, случайная последовательность - 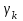 , где k - секретный ключ, а шифрованный текст с, то имеем , где k - секретный ключ, а шифрованный текст с, то имеем  . .Такая обратимость шифра может в ряде случаев быть использована противником для передачи ложных шифровок, даже не прибегая к раскрытию секретного ключа. Например, если линия связи недозагружена, но в тоже время аппаратура шифрования не выключается и в канал связи достаточно длительное время поступает чистая случайная последовательность 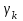 . Если в это время перехватить шифровку в виде чистого ключа . Если в это время перехватить шифровку в виде чистого ключа 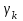 и наложить на нее свое сообщение, то получатель получит переданный ему перехватчиком текст ложного сообщения. А так как этот текст будет получен в шифрованном виде, то его содержимому могут поверить, что недопустимо. Даже если перехваченное сообщение не будет чистым ключом и наложить на нее свое сообщение, то получатель получит переданный ему перехватчиком текст ложного сообщения. А так как этот текст будет получен в шифрованном виде, то его содержимому могут поверить, что недопустимо. Даже если перехваченное сообщение не будет чистым ключом 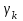 , и будут, конечно, некоторые искажения ложного шифрования, получатель может их интерпретировать как помехи в канале связи. , и будут, конечно, некоторые искажения ложного шифрования, получатель может их интерпретировать как помехи в канале связи.Шифры перестановки. При применении шифра замены символы исходного сообщения могут превращаться во что угодно, но сохраняют в шифротексте своё первоначальное положение, т.е. местоположение символа в исходном тексте такое же, как и в шифрованном тексте. Если теперь к шифротексту применить шифр перестановки, то местоположение символов в шифротексте может стать произвольным по отношению к расположению этих символов в исходном тексте. Это позволяет существенно увеличить стойкость шифра. Примерами шифров перестановки являются скиталь, магические квадраты и другие, о которых говорилось на первой лекции. Перестановка символов текста может осуществляться двумя способами: 1. Перестановка может делаться до наложения на сообщение случайной последовательности 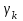 (т.е. до применения шифра замены). В этом случае шифрованное сообщение имеет вид (т.е. до применения шифра замены). В этом случае шифрованное сообщение имеет вид 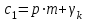 , где р - перестановка заданного типа. При таком, способе, если в канале связи отсутствует сообщение, т.е. m=0, то в канал попадает чистый ключ , где р - перестановка заданного типа. При таком, способе, если в канале связи отсутствует сообщение, т.е. m=0, то в канал попадает чистый ключ 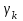 . .2. Перестановка может делаться после наложения на исходный текст случайной последовательности 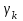 . .В этом случае  и при отсутствии сообщения, т.е. при m=0, в канал связи поступает ключ и при отсутствии сообщения, т.е. при m=0, в канал связи поступает ключ 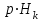 , подвергнутый шифрованию перестановкой. , подвергнутый шифрованию перестановкой.Перестановка может осуществляться отдельными битами или такими группами бит, как байт или блок. Временная сложность перестановки оценивается квадратом числа переставляемых элементов. Поэтому перестановка бит будет в 64 раза сложнее, чем перестановка байтами. Вычислительных способов перестановок существует очень много. Например, широко применяется перестановка по номерам N от 0 до L-1 на основе рекуррентного соотношения 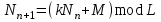 , ,где а) К и М берутся из интервала (1,L -1) б) М - взаимно простое L в) К -1 делится на любой простой делитель L г) К -1 делится на 4,если L делится на 4. Для хорошего запутывания такую перестановку делают несколько раз, выбирая каждый раз K и М случайным образом. Шифр замены, осложненный перестановкой, обладает достаточно высокой стойкостью. Его вскрытие без знания ключа неоднозначно, что не позволяет сколько-нибудь уверенно расшифровать сообщение. Существенно повысить стойкость шифра можно, если вместо перестановки использовать линейное преобразование вида с=Lm, где L -невырожденная матрица случайного линейного преобразования (или, что тоже самое, детерминант L не равен нулю). Шифры на основе этого преобразования получили название скремблеров или взбивалок. Шифры взбивания. Для шифров этого типа характерным является зависимость каждого бита шифротекста от каждого бита исходного текста. Детерминант случайной матрицы L, также как и её элементы может принимать два значения 0 и 1. Если 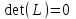 , матрица является вырожденной. Основной проблемой использования шифра взбивания является стремительное убывание числа невырожденных матриц с увеличением их размера. Для получения случайных невырожденных матриц специалистами фирмы IBM при сознании криптосистемы Lucifer, ставшей впоследствии (1976 год) национальным стандартам шифрования США под именем DEC, был предложен достаточно эффективный способ, не требующий много вычислений. Суть одного шага этого способа сводится к следующему: , матрица является вырожденной. Основной проблемой использования шифра взбивания является стремительное убывание числа невырожденных матриц с увеличением их размера. Для получения случайных невырожденных матриц специалистами фирмы IBM при сознании криптосистемы Lucifer, ставшей впоследствии (1976 год) национальным стандартам шифрования США под именем DEC, был предложен достаточно эффективный способ, не требующий много вычислений. Суть одного шага этого способа сводится к следующему: Входной блок данных делится на две равные части: левую  и правую и правую 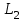 . После этого формируется выходной массив так, что его правая часть . После этого формируется выходной массив так, что его правая часть  представляется левой частью представляется левой частью  исходного массива данных, а левая часть исходного массива данных, а левая часть 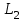 формируется как сумма по модулю 2 формируется как сумма по модулю 2  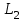 . Далее выходной массив шифруется перестановкой. Все проведенные операции обратимы и расшифрование осуществляется за число операций, линейно зависящих от размерности задачи. После нескольких таких шагов взбивания можно считать, что каждый бит выходного блока шифровки может зависеть от каждого бита исходного сообщения. Существенным недостатком шифра взбивания является тот факт, что с увеличением числа шагов взбивания искажение (порча) единственного бита в шифротексте делает нечитаемым половину текста при побайтной перестановке. Если перестановку осуществлять побитно, то от ошибки в одном бите перестал бы читаться весь текст. . Далее выходной массив шифруется перестановкой. Все проведенные операции обратимы и расшифрование осуществляется за число операций, линейно зависящих от размерности задачи. После нескольких таких шагов взбивания можно считать, что каждый бит выходного блока шифровки может зависеть от каждого бита исходного сообщения. Существенным недостатком шифра взбивания является тот факт, что с увеличением числа шагов взбивания искажение (порча) единственного бита в шифротексте делает нечитаемым половину текста при побайтной перестановке. Если перестановку осуществлять побитно, то от ошибки в одном бите перестал бы читаться весь текст.Шифры с открытым ключом. В традиционных криптографических системах одним и тем же секретным ключом осуществляется как шифрование, так и расшифрование сообщений. Это предполагает, что отправитель и получатель сообщения получают идентичные копии ключа курьером. Это достаточно дорогостоящий способ и он почти неприменим для коммерческих фирм и практически недоступен для частных лиц. В 1976 году Диффи и Хеллман предложили схему открытого распределения ключей, которая позволяет решить указанную проблему. Эта схема предполагает независимое генерирование каждым из пары связывающихся пользователей своего случайного числа, преобразование его посредствам определенной процедуры (об этом мы более подробно поговорим на следующих лекциях), обмен преобразованными числами по открытому каналу связи и вычисление каждым пользователем общего секретного ключа. Такой секретный ключ существует только в течение одного сеанса связи. Таким образом, использование схемы открытого распределения ключей позволяет каждой паре абонентов самим выбирать свой общий секретный ключ и тем самым упрощает процедуру распределения секретных ключей. Вместе с тем, такая схема не устраняет необходимости аутентификации, т.е. подтверждения того, что, скажем, абонент А получил сообщение именно от абонента B, а не от какого-либо нарушителя. Поэтому каждый абонент все же должен иметь свой секретный ключ или пароль, известный только ему и отличающий его от всех остальных абонентов. Необходимость в системах открытого распределения ключей иметь заранее распространенные из центра индивидуальные секретные пароли не выглядит столь уже дорогостоящей задачей как изготовление и распределение из центра секретных ключей. Во-первых, срок действия того пароля может быть весьма длительным, например, 1 год. Кроме того, в некоторых видах связи подтверждение подлинности партнера может достигаться за счет узнавания его по физическим признакам (по голосу при телефонной связи, по внешнему виду и голосу в системах телевизионной связи и т.д.). Наряду с этим в системах с открытым ключом в каждом узле связи (т.е. у каждого абонента) достаточно иметь один секретный ключ, в то время как в классических криптосистемах в каждом узле находится столько ключей, сколько этот узел имеет абонентов. В качестве индивидуального секретного ключа в современных системах связи используется так называемая цифровая подпись, о которой более подробно будем говорить на следующих лекциях. Представленное выше рассмотрение различных типов шифров позволяет сделать ряд выводов. Крайне желательно, чтобы как можно меньший объем информации шел по закрытому каналу, требующему больших затрат и являющемуся наименее надежным участком системы связи. Однако совсем обойтись без него нельзя, так как он необходим для передачи секретных ключей. Сложность подбора ключа зависит лишь от объема информации, которую он занимает. Чем больше информации в ключе, тем сложнее его подобрать. Таким образом, существует объективное противоречие между сокращением информации, передаваемой по секретному каналу и увеличением информации в секретном ключе, чтобы повысить сложность его раскрытия. Это ставит серьезную проблему поиска оптимального объема информации содержащегося в секретном ключе. Нераскрываемых шифров не существует. Все шифры просто делают процедуру взламывание шифротекстов либо заведомо дороже содержащейся в сообщении информации, либо затягивают время расшифрования до неприемлемых размеров. При разработки шифров устанавливают требуемые цену или время взламывания, и затем уже не обращают внимание на очень богатых или терпеливых взломщиков. Необходимую сложность ключа вычислить можно, если знать технические возможности взломщика и плату за ошибку оценки надежности шифра. Например, взломщик вручную не переберет и сотни ключей при расшифровке ключа, поэтому скажем тысяча вариантов ключа в этом случае вполне достаточно для его надежной защиты. Это эквивалентно информационной длине ключа десять бит (число вариантов ключа при этом будет 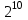 =1024) или ключевому слову из 3 -5 букв. Подводя итоги сказанному, можно сказать, что в настоящее время в криптографии используют два основных вида шифров - шифры замены, шифры перестановки и различные их комбинации. При этом операция шифрования редко применяется ко всему сообщению в целом. Обычно сообщение разбивается на большое число фрагментов, называемых блоками, фиксированного размера и каждый блок шифруется отдельно, если не независимо. Это существенно упрощает процедуру шифрования, так как сообщение обычно имеют различную длину. Таким образом, можно выделить три основных типа криптосистем используемых в современной криптографии: поточные, блочные и системы с открытым ключом. =1024) или ключевому слову из 3 -5 букв. Подводя итоги сказанному, можно сказать, что в настоящее время в криптографии используют два основных вида шифров - шифры замены, шифры перестановки и различные их комбинации. При этом операция шифрования редко применяется ко всему сообщению в целом. Обычно сообщение разбивается на большое число фрагментов, называемых блоками, фиксированного размера и каждый блок шифруется отдельно, если не независимо. Это существенно упрощает процедуру шифрования, так как сообщение обычно имеют различную длину. Таким образом, можно выделить три основных типа криптосистем используемых в современной криптографии: поточные, блочные и системы с открытым ключом.Их основными различиями являются следующие. 1. При поточном шифровании каждый знак шифротекста является функцией значения и положения знака открытого текста. Знаками бывают биты, байты и редко единицы текста крупнее этих. Поточные криптосистемы обычно используют шифры замены. 2. При блочном шифровании исходный текст разбивается на равные по длине блоки бит. К блокам применяется зависящие от ключа тип шифра для их преобразования в блоки шифровки той же длины. Обычно блоки шифруются перестановкой или взбиванием. 3. Основное отличие криптосистем с открытым ключом состоит в том, что знание алгоритма и ключа шифрования не достаточно для расшифровки сообщения. Потоковые криптосистемы широко используются в военных и других системах близких к ним по назначению для шифрования данных и преобразованных в цифровую форму речевых сигналов. Это связано, прежде всего, с относительной простотой конструирования и реализации генераторов псевдослучайных, шифрующих последовательностей на базе теории линейных рекуррентных последовательностей над конечными полями и других математических дисциплин. Однако главным фактором такого применения поточных криптосистем является отсутствие размножения ошибок. Так как при передаче данных и речевых сообщений в стратегической связи используются каналы недостаточно высокого качества, то любая криптосистема, которая увеличивает и без того нередкие ошибки, неприменима. Кроме указанных приложений поточные криптосистемы используются и при передаче данных в локальных и глобальных сетях ЭВМ, где их непрерывное действие препятствует эффективному криптоанализу. Главное свойство блочных криптосистем состоит в том, что каждый бит текста шифровки является функцией почти всех бит соответствующего блока открытого текста, и никакие два блока открытого текста не могут быть представлены одним и тем же блоком шифротекста. Основное их преимущество состоит в том, что даже небольшие изменения открытого текста или ключа вызывают большие и непредсказуемые изменения в шифротексте. Однако существенным их недостатком является распространение (размножение) ошибки внутри блока. Результатом изменения одного бита в принятом блоке будет неправильное расшифрование всего блока. Возможно образование комбинированных криптосистем поточного и блочного типа с использованием лучших свойств каждой из них. В таких системах поточное шифрование комбинируется с перестановками бит в блоках. Открытый текст сначала шифруется на основе шифра замены, а затем полученный шифротекст разбивается на блоки фиксированного размера и в каждом блоке дополнительно реализуется под управлением ключа шифр перестановки. В результате получается шифр, не размножающий ошибки, в котором неизвестно, какому биту открытого текста соответствует бит шифровки, что существенно повышает стойкость криптосистемы. Криптосистемы с открытым ключом обычно представляют собой систему блочного шифрования, оперирующую с блоками большой длины. Это обусловлено тем, что криптоаналитик, знающий открытый ключ шифрования мог бы предварительно вычислить и составить таблицу соответствия блоков открытого текста блокам шифровки. Если длина блоков мала, то число возможных блоков будет не слишком большим и может быть составлена полная таблица, дающая возможность мгновенного расшифрования любого шифротекста с использованием известного отрытого ключа. Ни один алгоритм шифрования с открытым ключом не может быть применен для каналов с большой скоростью. Это значит, что использование таких систем для блочного шифрования ограничено лишь распространением ключей, аутентификацией и формированием цифровой подписи. Общую характеристику существующих криптосистем можно представить в виде следующей таблицы
После характеристики в общем виде различных типов шифров и классов криптосистем перейдем к непосредственному рассмотрению алгоритмов криптографии. 11. Методы формирования псевдослучайных |
