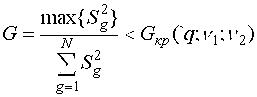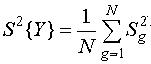Для проверки гипотезы об однородности оценок дисперсий следует пользоваться критерием Кохрена, который основан на законе распределения отношения максимальной эмперической дисперсии к сумме всех дисперсий, т.е.
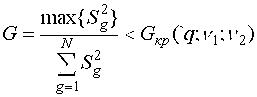
| (7) |
Если вычисленное значение критерия G окажется меньше табличного значения Gкр, найденного для q%-ного уровня значимости, vзн = v2 = N - числа степеней свободы знаменателя (например для q=5%; vчисл = 3 - 1 = 2; vзн=8, Gкр = 0,5157, см. табл.П.5), то гипотеза об однородности дисперсий принимается. При этом всю группу дисперсий S2g можно считать оценкой S2{Y} одной и той же генеральной дисперсии воспроизводимости 2{Y}, откуда
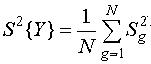
| (8) |
Если проверка на воспроизводимость дала отрицательный результат, то остается признать либо невоспроизводимость эксперимента относительно управляемых переменных вследствие наличия флуктуаций неуправляемых и неконтролируемых переменных, создающих на выходе большой уровень "шума", либо наличие грубого промаха в строке, откуда взята дисперсия max{S2g}. В первом случае следует увеличить число параллельных опытов, во втором - найти грубый промах и заменить его на результат доброкачественного измерения при соответствующей комбинации факторов. Если это по каким-то причинам невозможно, то, чтобы не нарушать предпосылки использования критерия Кохрена, на место грубого промаха следует поместить среднюю арифметическую величину 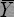 g данной строки. g данной строки.
Следует также отметить, что критерий Кохрена можно применять не к любой группе выборок, а только к группе выборок одинакового объема, что как раз и имеет место при полном факторном эксперименте.
Легко заметить, что исходный план (табл.1) содержит много больше строк, чем столбцев и, следовательно, из результатов эксперимента согласно условию решения нормальных уравнений (2) можно получить дополнительную информацию, т.е. расширить модель. Безусловно, это относится к средней арифметической всего эксперимента, т.е. к отклику в базовой точке b0, для расчета которого можно ввести фиктивную переменную xод = +1 для всех строк. Оставшиеся свободными столбцы можно использовать для нахождения оценок коэффициентов при парных взаимодействиях и т.п. При этом соответствующие величины xixj, xixjxl получаются простым перемножением соответствующих столбцов исходного плана.
Тогда математическая модель объекта, получающаяся в результате ПФЭ может быть представлена в виде
Y = 0 + 0x1 + nxn + 12x1x2 + (n-1)x1x2 + 123x1x2x3 + 123...nx1x2x3x3
| (9) |
Однако вследствие того, что из ограниченного числа опытов нельзя получить точные значения коэффициентов i, а только их независимые оценки bi, вся математическая модель становится оценочной
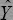 = b0 + b1x1 +...+ bnxn + b12x1x2 + b1...nx1...xn = b0 + b1x1 +...+ bnxn + b12x1x2 + b1...nx1...xn
| (10) |
Пример матрицы планирования, принципа ее реализации и последующей обработки экспериментальных данных приведен в табл.2 на базе трехфакторного эксперимента. В разделе "Матрица планирования эксперимента" включены не только относительные переменные xi, сочетание которых и является собственно настоящей матрицей планирования, ни и их парные и тройные взаимодействия, знание которых необходимо лишь на этапе обработки экспериментальных данных.
Таблица 2
|
Матрица планирования ПФЭ типа N=23 и обработка его результатов
|
номер
строки
g
|
Порядок реализации опытов
|
Матрица планирования эксперимента
|
Результаты эксперимента
|
Первичная
обра ботка
результатов
|
Проверка
адекватности
|
l
|
z0
|
z1
|
z2
|
z3
|
z4
|
z5
|
z6
|
z7
|
Yg1
|
...
|
Ygl
|
...
|
Ygm
|
 g g
|
S2g
|
 g g
|
(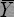 g- g-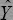 g)2 g)2
|
k1
|
...
|
kl
|
...
|
km
|
x0
|
x1
|
x2
|
x3
|
x1x2
|
x1x3
|
x2x3
|
x1x2x3
|
1
|
1
|
...
|
6
|
...
|
8
|
+
|
-
|
-
|
-
|
+
|
+
|
+
|
-
|
|
|
|
|
|
|
|
|
|
2
|
7
|
...
|
5
|
...
|
4
|
+
|
+
|
-
|
-
|
-
|
-
|
+
|
+
|
|
|
|
|
|
|
|
|
|
3
|
3
|
...
|
7
|
...
|
6
|
+
|
-
|
+
|
-
|
-
|
+
|
-
|
+
|
|
|
|
|
|
|
|
|
|
4
|
8
|
...
|
2
|
...
|
7
|
+
|
+
|
+
|
-
|
+
|
-
|
-
|
-
|
|
|
|
|
|
|
|
|
|
5
|
6
|
...
|
3
|
...
|
2
|
+
|
-
|
-
|
+
|
+
|
-
|
-
|
+
|
|
|
|
|
|
|
|
|
|
6
|
4
|
...
|
4
|
...
|
1
|
+
|
+
|
-
|
+
|
-
|
+
|
-
|
-
|
|
|
|
|
|
|
|
|
|
7
|
2
|
...
|
1
|
...
|
5
|
+
|
-
|
+
|
+
|
-
|
-
|
+
|
-
|
|
|
|
|
|
|
|
|
|
8
|
5
|
...
|
8
|
...
|
3
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
+
|
|
|
|
|
|
|
|
|
| |
 Скачать 446.5 Kb.
Скачать 446.5 Kb.