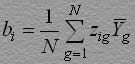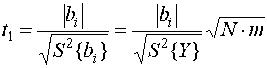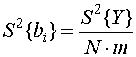моделирование. Математическое моделирование при активном эксперименте
 Скачать 446.5 Kb.
|
|
Для удобства расчетов и представления формул каждый столбец может быть представлен в виде новой переменной Zig. Тогда оценки коэффициентов уравнения регрессии легко найти по формуле
Легко заметить, что матрица планирования  является ортогональной с линейно независимыми вектор-столбцами; отсюда следует диагональность матрицы нормальной системы уравнений, а следовательно, и взаимная независимость оценок коэффициентов уравнения регрессии.Необходимо отметить, что получаемая модель не дает членов типа x2ii и, таким образом, является неполной. В большинстве случаев это не отражается на качестве модели, так как чаще всего bii=0. Однако в случаях, когда bii0, модель становится неточной (неадекватной), тогда следует от ПФЭ переходить к другим принципам планирования (как правило, это случается в окрестностях частного или глобального экстремума целевой функции). После определения оценок коэффициентов регрессии необходимо проверить гипотезу о значимости коэффициентов bi. Лучше всего это сделать в виде нуль-гипотезы, т.е. гипотезы о равенстве bi = 0. Если она подтвердилась, то коэффициент bi следует признать статистически незначимым и отбросить из искомой модели; если гипотеза не подтвердилась, то соответствующий коэффициент bi следует признать значимым и включить в модель. Проверка гипотезы проводится с помощью t - критерия Стъюдента, который при проверка нуль-гипотезы формируется в виде
где S2{bi}- дисперсия ошибки определения коэффициента bi. При полном и дробном факторном планировании для всех i
|
