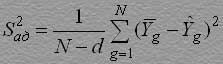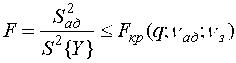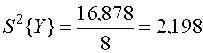моделирование. Математическое моделирование при активном эксперименте

• Название: Математическое моделирование при активном эксперименте
• Дата: 19.12.2022
• Размер: 446.5 Kb.
• Имя файла: моделирование.doc
• Тип: Курсовая; #852876
• страница: 6 из 9

Если вычисленная величина параметра t_i превышает табличное значение t_кр, найденное для q%-ного уровня значимости и v_з=N(m-1) числа степеней свободы (например для q = 5%; v_з = 16; t_кр = 2,199, см.табл.П.2) то нуль-гипотеза отвергается и коэффициент считается незначимым и его следует отбросить, не включая в искомую модель.

Статистическая незначимость коэффициента bi может быть обусловлена следующими причинами:

1. 
   уровень базового режима ^* близок к точке частного экстремума по переменной X_i или по произведению переменных;
   
2. 
   шаг варьирования X_i выбран малым;
   
3. 
   данная переменная (или произведение переменных) не имеет функциональной связи с выходным параметром Y;
   
4. 
   велика ошибка эксперимента вследствие наличия неуправляемых и неконтролируемых переменных.
   

Поскольку ортогональное планирование позволяет определять доверительные границы для каждого из коэффициентов регрессии в отдельности, то, если какой-либо из коэффициентов окажется незначимым, он может быть отброшен без пересчета всех остальных. После этого математическая модель объекта составляется в виде уравнения связи выходного параметра Y и переменных x_i, включающего только значимые коэффициенты.

Чтобы проверить гипотезу об адекватности представления результатов эксперимента найденному уравнению связи (иными словами, чтобы проверить, насколько найденное уравнение соответствует экспериментальным результатам), достаточно оценить отклонение выходной величины Y_g, предсказанное уравнением регрессии, от результатов экспериментов _g в точках факторного пространства.

Рассеяние результатов эксперимента вблизи уравнения связи, аппроксимирующего искомую функциональную зависимость, можно охарактеризовать с помощью дисперсии неадекватности ²_ад, оценка которой S²_ад находится по формуле

(14)

с числом степеней свободы v_ад = N-d, где d - число членов аппроксимирующего полинома.

Проверка адекватности состоит в выяснении соотношения между дисперсией неадекватности ²_ад и дисперсией воспроизводимости ²{Y}. Если ²_ад не превышает дисперсии опыта, то полученная математическая модель адекватно представляет результаты эксперимента, если же ²_ад> ²{Y}, то описание считается неадекватным объекту.

Проверка гипотезы об адекватности проводится с использованием F-критерия Фишера.

Критерий Фишера позволяет проверить нуль-гипотезу о равенстве двух генеральных дисперсий ²_ад и ²{Y}. В связи с тем, что самих генеральных дисперсий мы не знаем, F-критерий формируется как отношение

(15)

Если вычисленное по формуле (15) значение критерия F меньше табличного F_кр, найденного для q%-ного уровня значимости, v_числ = v_ад = v₄ = N-d числа степеней свободы числителя и v_зн = v_з = N(m-1) числа степеней свободы знаменателя, то нуль-гипотеза принимается. В противном случае она отвергается и описание (модель) признается неадекватным объекту. Некоторые значения F_кр(q=5%;v₄;v_з) приведены в табл.П.4

В ходе работы может возникнуть ситуация, когда выборочная дисперсия неадекватности S²_ад не превосходит оценки дисперсии воспроизводимости S²{Y} (т.е. когда S²_адS²{Y}). Тогда соотношение (15) будет равно F1 и неравенство Fкр выполняется для любого числа степеней свободы v₄ и v₃, т.е. гипотеза ²_ад ²{Y} не противоречит выборочным данным и математическая модель адекватно представляет объект.

Проверка адекватности возможна только при v_ад = v₄ > 0. Число вариантов варьирования плана ПФЭ равно числу оцениваемых коэффициентов регрессии уравнения связи (N = d). Следовательно, не остается степеней свободы (v_ад = 0) для проверки нуль-гипотезы об адекватности представления экспериментальных данных выбранной формой аппроксимирующего полинома. Если же некоторые коэффициенты регрессии оказались незначимыми или ими можно пренебречь в силу их малости, то число членов проверяемого уравнения в этом случае будет меньше числа вариантов варьирования (dад>0) останется для проверки гипотезы адекватности.

Если гипотеза адекватности отвергается, то модель признается неадекватной экспериментальным данным. Неадекватность модели не означает ее неправильности! Неадекватность модели может означать, что не весь перечень влияющих факторов был принят во внимание, или что необходимо перейти к более сложной форме уравнения связи, или выбрать другой шаг варьирования по одному или нескольким факторам и т.п. Однако все достижения неадекватной модели: отсев незначимых факторов, оценка дисперсии эксперимента и др. остаются в силе.

 

Пример 1. Методом ПФЭ найти математическую модель процесса напыления резисторов.

После консультации с экспертами и некоторых предварительных исследований было определено, что на величину сопротивления напыляемых резисторов могут оказывать влияние следующие факторы:

1. 
   Состояние испарителя - "чистое", т.е. порошок для напыления сыпется в стакан испарителя впервые после промывки его сторон, или "грязное", т.е. порошок сыпется в испаритель, в котором осталось некоторое его количество от предыдущего цикла напыления; обозначим этот фактор как x1, причем величина x₁ = +1соответствует "чистому", а величина x₁ = -1 соответствует "грязному" состоянию испарителя;
   
2. 
   Температура подогрева подложки x₂, причем x₂ = +1 соответствует верхней допустимой по техпроцессу температуре, а x₂ = -1 - нижней;
   
3. 
   Температура испарителя x3, причем x₃ = +1 соответствует верхней допустимой по техпроцессу температуре, а х₃ = -1 - нижней.
   

План эксперимента, его пятикратная реализация с учетом рандомизации и первичная обработка результатов представлена в таблице.

номер строки g	Циклы					z0	z1	z2	z3	z4	z5	z6	z7	Результаты, кOм					Обработка		Адекватность
																			g	S2g	g	( g- g)2
	k1	k2	k3	k4	k5	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	Yg1	Yg2	Yg3	Yg4	Yg5
1	4	2	3	6	8	+	-	-	-	+	+	+	-	11,4	10,5	13,8	14,0	12,1	12,36	2,303	12,10	0,0676
2	3	3	6	2	5	+	+	-	-	-	-	+	+	18,1	17,4	15,2	16,8	19,2	17,34	2,228	17,08	0,0676
3	8	6	2	4	1	+	-	+	-	-	+	-	+	10,8	9,3	11,6	12,1	9,8	10,72	1,387	10,98	0,0676
4	6	1	7	1	6	+	+	+	-	+	-	-	-	18,8	29,6	22,0	22,8	20,7	21,38	2,752	21,64	0,0676
5	5	8	1	3	4	+	-	-	+	+	-	-	+	12,9	12,8	13,6	15,2	14,0	13,70	0,950	13,98	0,0784
6	2	5	5	7	2	+	+	-	+	-	+	-	-	12,0	11,6	14,2	13,4	12,5	12,74	1,118	13,00	0,0676
7	1	7	4	8	7	+	-	+	+	-	-	+	-	15,1	14,8	16,8	18,1	17,0	16,36	1,913	16,10	0,0676
8	7	4	8	5	3	+	+	+	+	+	+	+	+	13,5	11,9	14,3	17,0	16,2	14,58	4,227	14,32	0,0676
																			119,18	16,878	-	0,5410

При первичной обработке результатов экспериментов пользуемся формулами (4) и (5), а затем проверяем воспроизводимость опытов по (7)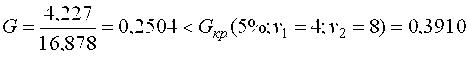



Таким образом, подтверждена воспроизводимость опытов (отсутствие в данных грубых промахов), что позволяет, в свою очередь, найти среднюю дисперсию строчных выборок (дисперсию опытов) по (8)

C

v3 = 8·(5-1) = 32 степенями свободы