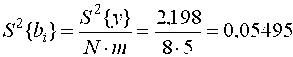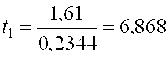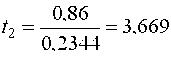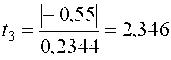моделирование. Математическое моделирование при активном эксперименте
 Скачать 446.5 Kb.
|
|
Оценки коэффициентов уравнения регрессии ищутся по формуле (11) 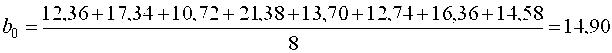 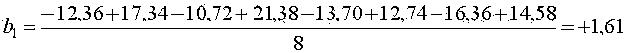 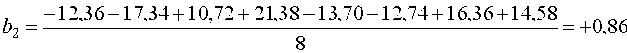 и т.д. Аналогично находим b3 = -0,55; b12 = +0,61; b13 = -2,30; b23 = +0,26; b123 = -0,81 Проверяем значимость оценок коэффициентов по критерию Стьюдента по формуле (12), предварительно найдя дисперсию оценок по формуле (13)
Табличное значение критерия ti (табл.П.2) tкр(5%;v3=32) = 2,046, поэтому все найденные оценки коэффициентов, кроме b23, признаются значимыми и должны войти в модель  = 14,90 + 1,61x1 + 0,86x2 -0,55x3 + 0,61x1x2 -2,30x1x3 - 0,81x1x2x3Для определения дисперсии адекватности по формуле (14) необходимо сначала найти числовые значения модели 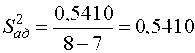g для каждой g-ой строки матрицы планирования, а затем подсчитать сумму квадратов разностей между модельным значением и средним арифметическим  g той же строки Тогда критерий Фишера (15) дает 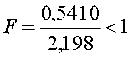 что доказывает адекватность найденной модели. Ее можно использовать для управления технологическим процессом испытания резисторов 2. Дробный факторный эксперимент Полный факторный эксперимент целесообразно использовать при сравнительно небольшом числе независимых факторов (обычно не больше 5), в противном случае число вариантов варьирования N = 2n становится непомерно большим и реализация эксперимента затрудняется. В то же время в большинстве практических задач взаимодействия внешних порядков, начиная с третьего (а то и второго), отсутствуют или пренебрежимо малы, вследствие чего излишне много степеней свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику). Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ позволяет получить приближение искомой функциональной зависимости Y = f(X1,...,Xn) в некоторой небольшой окрестности точки базового режима при минимуме опытов. Так, для решения трехфакторной задачи можно ограничиться четырьмя вариантами (N = 4), если в планировании ПФЭ типа 22 произведение x1x2 приравнять к третьей независимой переменной x3. Такое планирование, представленное матрицей табл 3, позволяет оценить свободный член b0 и три коэффициента регрессии при линейных членах b1,b2,b3 (из четырех опытов нельзя получить более четырех коэффициентов).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
