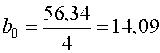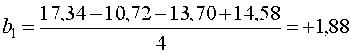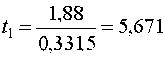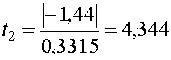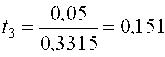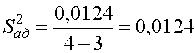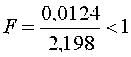моделирование. Математическое моделирование при активном эксперименте
 Скачать 446.5 Kb. Скачать 446.5 Kb.
|
|
Пример 2. Методом ДФЭ найти математическую модель процесса напыления резисторов. Воспользуемся результатами Примера 1 и положим в качестве генерирующего соотношения равениство x1 = x2x3 (т.к. b23 = 0). Тогда матрица планирования и результаты эксперимента (опуская промежуточные данные) будут выглядеть так
Проверим воспроизводимость опытов 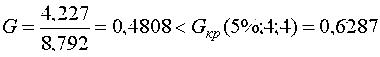 откуда следует, что результаты опытов получены правильно, дисперсия строчных выборок равна S2{y} = 8,792 / 4 = 2,198 с числом степеней свободы v3 = 4·4 = 16. Оценки коэффициентов уравнения регрессии
аналогично b2 = -1,44; b3 = 0,05. Проверка значимости полученных оценок начинается с определения их СКО 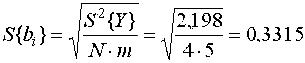 откуда
Табличные значения критерия tкр(5%;16) = 2,131, следовательно, модель найдена в виде Проверка адекватности модели дает
т.е. модель признается адекватной экспериментальным данным. Сравнение моделей примера 1 и примера 2 показывает, что они имеют совершенно разный вид, а по некоторым факторам - противоположные по смыслу оценки коэффициентов. Отсюда можно сделать несколько общих выводов и рекомендаций (без подробного обоснования), пригодных для использования в рамках теории планирования экспериментов: по одним и тем же экспериментальным данным можно построить несколько математических моделей, каждая из которых будет адекватна для своего набора оценок коэффициентов регрессии; из всех моделей наилучшей признается та, у которой меньше членов и меньше критерий Фишера (или, если угодно, меньше дисперсия адекватности); при большом числе факторов работу по математическому моделированию следует начинать с ДФЭ возможно большей дробности. Если модель получилась неадекватной, ее всегда можно достроить до следующей реплики вплоть до ПФЭ. Это сэкономит количество опытов, время, затраты и т.п. Заключение. Применение описанных выше методов математического моделирования полностью оправдало себя в условиях с небольшим числом факторов. Но при очень большом числе факторов и привлечение их к составлению математического описания исследуемого объекта методами ПФЭ или ДФЭ может потребовать увеличения объема экспериментальной работы, что редко может выполняться из-за экономических, технологических и прочих ограничений. Таким образом, возникает необходимость в предварительном отсеивании несущественных и выделении тех факторов процесса, которые оказывают наиболее заметное влияние на целевую функцию. Другим существенным затруднением для применения ПФЭ или ДФЭ в производственных условиях является метод получения оценок коэффициентов регрессии. Оценки вида (11) считаются оптимальными в смысле эффективности (минимума дисперсии), поскольку их вычисление базируется на методе наименьших квадратов, однако предварительным условием такой оптимальности являются требования независимости факторов, ортогональности и симметричности плана эксперимента, а также требование равенства дисперсий условных распределений плотности вероятности f(y/xk). В свою очередь симметричность плана требует равного количества наблюдений, соответствующих положительным и отрицательным значениям k-го фактора. На практике в производственных условиях требования симметричности плана и равенства дисперсий условных распределений плотности вероятности f(y/xk) эксперимента, как правило, нарушаются, особенно в случаях, когда исследователь пытается построить модель по результатам, зафиксированными для случайной системы комбинаций производственных факторов. При этом всегда имеется выбор: либо нарушить одно из требований факторного анализа, либо потерять часть информации, пытаясь выбрать из нее только то, что согласуется с правилами ведения ПФЭ (ДФЭ). |