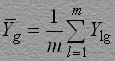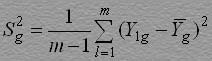моделирование. Математическое моделирование при активном эксперименте

• Название: Математическое моделирование при активном эксперименте
• Дата: 19.12.2022
• Размер: 446.5 Kb.
• Имя файла: моделирование.doc
• Тип: Курсовая; #852876
• страница: 3 из 9

Следует отметить, что суть матрицы не изменится, если первая строка ₁ будет выбрана так, чтобы управляемые переменные находились на верхнем уровне, т.е. x_i1 = +1.

Матрицы планирования любого другого типа, например, 2⁴, 2⁵ и т.д. могут быть получены описаным выше способом.

Поскольку изменение выходной величины Y носит случайный характер, необходимо в каждой точке _g (т.е. в точке с координатами, записаными в g-й строке) проводить m параллельных опытов и результаты наблюдений Y_1g,Y_2g,...,Y_mg усреднять

(4)

Величина m может быть любой, но не меньше m=3. Тогда эксперимент делится на m серий опытов, в каждой из которых полностью реализуется матрица планирования (т.е. эксперимент проводится в N=2ⁿ точках факторного пространства).

Одним из важнейших положений современной теории планирования эксперимента является рандомизация. План эксперимента составляется так, чтобы рандомизировать, т.е. сделать случайными те систематически действующие факторы, которые трудно поддаются учету и контролю, для того, чтобы рассматривать их как случайные величины и учитывать статистически.

Перед реализацией плана на объекте необходимо произвести рандомизацию - с помощью таблицы равномерно распределенных случайных чисел (табл.П.6) определить последовательность реализации матрицы планирования в каждой из m серий опытов. Для этого в качестве начала выбирается любое число из табл.П.6 и записывается в столбец k₁ из табл.2 на место g=1. Остальные места этого столбца заполняют числа от 1 до N, следующие по порядку из табл.П.6 за выбранным начальным. Следует обращать внимание на то, чтобы числа в столбцах табл.2 не повторялись дважды. Пусть, например, при g=4 k₁₄=8, это значит, что в первой серии испытаний точка ₄ реализуется восьмой по порядку.

Аналогично рандомизируются испытания в каждой из оставшихся серий экспериментов; порядок реализации записывается в столбцах k₂,k₃,...,k_m. Результаты эксперимента в каждой из серий испытаний записываются в столбцах Y₁,Y₂,...,Y_m.

Проверка воспроизводимости - это проверка на выполнение второй предпосылки регрессионного анализа об однородности выборочных дисперсий S²_g. Задача состоит в проверке гипотезы о равенстве дисперсий ²{Y₁}²{Y₂}²{Y_N} при экспериментах соответственно в точках ₁, ₂,..., _g,..., _N.

Оценки дисперсий находятся по формуле

(5)

Так как все дисперсии получены по выборкам одинакового объема m, то число степеней свободы для всех дисперсий одинаково и равно

v1 = m-1

(6)