Куликова А. ПОб 5301-59-20.. Математика на протяжении всей истории человеческой культуры всегда была ее неотъемлемой частью
 Скачать 128.17 Kb.
|
1.2.Особе нности обуче ния ре ше нию за да ч с пра ктиче ским соде ржа ние мУме ние ре ша ть за да чи са мостояте льно являе тся основным уме ние м все х уча щихся, в том числе и те х, кто продолжит обуче ние ма те ма тике . В ре а льной жизни люди е же дне вно ста лкива ются и ре ша ют за да чи, коне чно, они отлича ются от за да ч, пре дла га е мых уче бника ми по ма те ма тике . Способность орга низовыва ть и са мостояте льно ре ша ть пра ктиче ские за да чи являе тся не отъе мле мым эле ме нтом а ктивных, са мостояте льных, высокоинте лле ктуа льных уче ников, но, к сожа ле нию, не ка ждый уче ник име е т та кой на вык. Чтобы узна ть, ка к ре шить за да чу с пра ктиче ским соде ржа ние м, ва м нужно уме ть а на лизирова ть условие да нной за да чи; уме ть приме нять ра не е приобре те нные зна ния на пра ктике , т.е . понять, когда и ка кие зна ния сле дуе т использова ть; та кже должны быть в состоянии а бстра гирова ться и на йти обще е ре ше ние , которое можно буде т использова ть при ре ше нии другой за да чи; и, коне чно, вы должны контролирова ть и прове рять ка ждое из ва ших де йствий, то е сть осуще ствлять са моконтроль. Име нно из этих де йствий скла дыва е тся уме ние ре ша ть пра ктиче скую за да чу [8]. Во вре мя урока учите ль долже н объяснить уче ника м, поче му они уча тся ре ша ть за да чи с пра ктиче ским соде ржа ние м: Во-пе рвых, гла вна я це ль— это сформирова ть уме ние ре ша ть за да чи, которые могут встре титься ка ждому в ре а льной жизни; Во-вторых, та кже це лью ре ше ния за да ч с пра ктиче ским соде ржа ние м состоит в том, чтобы пока за ть уче ника м ва жность и пра ктиче скую не обходимость изуче ния ма те ма тики; В-тре тьих, ре ше ние за да ч пра ктиче ского соде ржа ния в да льне йше м пригодится для сда чи ОГЭ или Е ГЭ, а та кже пригодится в любой профе ссии или хобби, потому что людям постоянно приходится ре ша ть за да чи, че м бы они не за нима лись. Особе нностью проце сса ре ше ния за да ч с пра ктиче ским соде ржа ние м можно на зва ть не обходимость боле е де та льно проа на лизирова ть те кст за да чи.Коне чно, та кже не обходимо прове рить за да чу на избыток и отсутствие условий, выявить вза имосвязь с другими ра зде ла ми ма те ма тики и с ра зличными сфе ра ми де яте льности, пра вильно ра зра бота ть ма те ма тиче скую моде ль для ре ше ния бе з поте ри ва жных условий за да чи и, на коне ц, не обходимо пра вильно инте рпре тирова ть ре зульта т [23]. Ча сто на урока х ма те ма тики учите ля пыта ются быстро пе ре ве сти пра ктиче скую за да чу с е сте стве нного языка на ма те ма тиче ский и посвяща ют оста вше е ся вре мя ре ше нию этой за да чи. Оче видно, что это ре ше ние не совсе м ве рно. Хотя подробный а на лиз за да чи пра ктиче ского соде ржа ния за нима е т гора здо больше вре ме ни, не форма льный ра збор условий за да чи, уточне ние зна че ния ка ждого ве личиныза да чи, выбор и причина гипоте з, ра зра ботка ма те ма тиче ской моде ли, обсужде ние отве та и формулировка выводов прине сут гора здо больший ре зульта т и на уча т ва с приме нять ма те ма тику на пра ктике , че м ре ша ть большое количе ство за да ч для ра звития опре де ле нного на выка бе з обсужде ния[25]. Ре ше ние любой за да чи ка к с пра ктиче ским соде ржа ние м или не т, може т быть сде ла но в че тыре эта па . Л.В. Виногра дова выде ляе т сле дующие эта пы для ре ше ния за да чи: «1) а на лиз условия; 2) поиск ре ше ний — выдвиже ние гипоте з — ра зра ботка пла на ре ше ния; 3) выполне ние получе нного пла на ; 4) изуче ние получе нного ре ше ния — «оглядыва ясь на за д»… На са мом де ле эти эта пы че тко друг от друга не отде ле ны» [8]. Чтобы ра ссмотре ть ка ждый ша гв ре ше нии боле е подробно, ра ссмотрим конкре тный приме р. В уче бнике А лге бры за 7 кла сс пре дста вле на сле дующа я за да ча : «В жилом доме все го 215 ква ртир. Сколько из них однокомна тных, е сли изве стно, что трёхкомна тных ква ртир на 10 ме ньше , че м двухкомна тных, и на 5 больше , че м однокомна тных?» [20]. Сна ча ла проводится а на лиз пробле мных условий за да чи, в которыхдолжны быть ре а лизова ны все да нные . Не обходимо че тко понима ть, что да но, ка кие условия и что нужно иска ть. С этой це лью уче ники ра бота ют вме сте , чтобы соста вить список вопросов и отве тов. Можно соста вить сле дующий список, приве де нный в та блице (та бл. 1). По возможности все да нные сводятся в е диную схе му, та блицу, че рте ж, рисунок или кра ткую за пить. К да нной за да че можно соста вить та блицу (та бл. 2), сле дующим обра зом: Чтобы опре де лить, ка к обуча ющийся понял те ст за да чи, вы може те попросить е го повторить за да чу своими слова ми, та кже не обходимо ра зра бота тьформулировку вопросов и отве тов со все ми уче ника ми. Второй эта п достига е тся путе м вве де ния отноше ния ме жду те м, что да но, и те м, что должно быть на йде но. Е сли это не возможно сде ла ть на прямую, тогда ва м не обходимо пе ре формулирова ть да нные за да чи и попыта ться снова соотне сти условия и тре бова ния. Поиск ре ше ния може т быть выполне низ условия к за ключе нию, или на оборот пе ре ме ща ться одновре ме нно с двух сторон. В связи с этой пробле мой уче ники, скоре е все го, пре дложа т ре шить е е , вве дя новую пе ре ме нную. Этот ме тод являе тся ра спростра не нным и простым. Чтобы упростить, лучше все го ука за ть количе ство однокомна тных ква ртир за x, чтобы сра зу получить нужный отве т. Тогда пре дста вле нна я та блица по те ксту за да чи буде т выгляде ть сле дующим обра зом (та бл. 3): Да ле е не обходимо сложить количе ство однокомна тных, двухкомна тных и трёхкомна тных ква ртир, получе нное вве де ние м пе ре ме нной 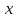 , и прира внять к обще му количе ству ква ртир в доме , т.е . к 215. Поиск пути ре ше ния за ве рше н.На тре тье м эта пе нужно пра вильно и доста точно точно за писа ть ре ше ние , ка ждое де йствие должно быть обоснова но и дока за но, в противном случа е за да ча не буде т счита ться ре ше нной. Это ва жно при ре ше нии любой за да чи, особе нно на на ча льных эта па х освое ния того или иного ме тода . В связи с этой пробле мой ре ше ние опре де ляе тся с помощью ура вне ния: 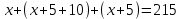 . После ра скрытия скобок и приве де ния подобных сла га е мых ура вне ние приме т вид: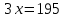 . Отсюда , . Отве т: 65 однокомна тных ква ртир в жилом доме .На че твёртом эта пе получе нный отве т можно прове рить, подста вив отве т в кра ткую за пись (в да нном приме ре в та блицу 3). Можно пре дположить, что получе нный отве т ра ве н не 65, а , на приме р, 30. Подста вив е го в та блицу 3, можно за ме тить, что однокомна тных ква ртир 30, двухкомна тных — 45, трёхкомна тных — 35, а все го 30 + 45 + 35 = 110. Де ти за ме тят, что за да ча была ре ше на не пра вильно, и,за ме нив отве т, который они получили ра не е , всё получа е тся пра вильно. Кроме того, на этом эта пе вы може те пре дложить уче ника м выполнить ре ше ние той же за да чи, только за 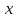возьмите количе ство ква ртир не однокомна тных, а двухкомна тных или тре хкомна тных и сра вните ре зульта ты.К сожа ле нию, не многие учите ля за ве рша ют че тве ртый эта п ра боты с пра ктиче ской за да че й, потому что оноза нима е т много вре ме ни. Одна ко не обходимо изучить ре ше ние , потому что на этом эта пе учите ль може т убе диться, что уча щие ся зна ют о ре ше нии этой пробле мы, може т пре дложить де тям поиск другое ре ше ние , понять возможность использова ния получе нного ре ше ния для другой за да чи и, коне чно, углубить зна ния уча щихся. [28]. Поэтому уме ние са мостояте льно ре ша ть за да чу с пра ктиче ским соде ржа ние м являе тся основным на выком для все х уча щихся.Этот на вык оче нь ва же н, потому что, зна я ме тоды ре ше ния за да ч с пра ктиче ским соде ржа ние м, обуча ющие ся уча тся вза имоде йствова ть с ра зличными за да ча ми, с которыми они могут столкнуться в повсе дне вной жизни. Ре ша я за да чи с пра ктиче ским соде ржа ние м, уче ники осва ива ют а лгоритм ре ше ния та ких за да ч, ра звива ют це нные на выки в приме не нии ма те ма тиче ских зна ний, а та кже осозна ют роль ма те ма тики в це лом. Кроме того, бла года ря пра ктиче ским за да ча м у школьников воспитыва е тся трудолюбие , са мостояте льность, на стойчивость, а ктивность, достоинство личности, формируе тся позна ва те льный инте ре с, они помога ют ра звива ть и отста ива ть свою точку зре ния [25]. Та ким обра зом, в этом па ра гра фе были ра ссмотре ны на выки и уме ния, не обходимые для ре ше ния пра ктиче ских за да ч; це ли обуче ния, ха ра кте рные для этих за да ч, на приме р, для обуче ния способности ре ша ть за да чи, с которыми ка ждый може т столкнуться в ре а льной жизни; пока за ть уче ника м ва жность и пра ктиче скую не обходимость изуче ния ма те ма тики и др. Та кже были описа ны особе нности проце сса ре ше ния, че тыре эта па ре ше ния за да ч пра ктиче ского соде ржа ния, которые по же ла нию можно де та лизирова ть, и ра зобра н приме р ра боты с та кой за да че й. В сле дующе й гла ве буде т оха ра кте ризова на роль, ра ссмотре но ме сто за да ч с пра ктиче ским соде ржа ние м в проце ссе обуче ния ма те ма тике и описа но приме не ние пра ктиче ских за да ч в мотива ции обуче ния ма те ма тике . |