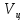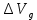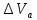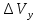механика полёта. Механика полета. Механика
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Отличие реальной скорости ракеты от характеристической Поскольку в условиях реального полёта на ракету кроме тяги двигателей действуют и другие силы, то скорость, развиваемая ракетами в этих условиях, как правило, ниже характеристической из-за потерь, вызываемых силами гравитации, сопротивления среды и др. Действительная скорость в конце активного участка траектории 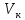 должна рассчитываться с учетом этих потерь: должна рассчитываться с учетом этих потерь: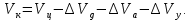 Формулу для расчета скорости 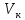 с учетом потерь называют иногда формулой Королева. с учетом потерь называют иногда формулой Королева.В таблице 1 приведён баланс скоростей ракеты Сатурн V при выводе корабля Аполлон на траекторию полёта к Луне. Таблица 1. Потери скорости
Как видно из таблицы 1, гравитационная составляющая является наибольшей в общей величине потерь. Гравитационные потери возникают из-за того, что ракета, стартуя вертикально, не только разгоняется, но и набирает высоту, преодолевая тяготение Земли, и на это также расходуется топливо. Величина этих потерь вычисляется по формуле: 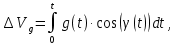 где 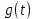 и и 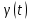 – местное ускорение гравитации и угол между вектором силы тяги двигателя и местным вектором гравитации, соответственно, являющиеся функциями времени по программе полёта. Как видно из таблицы 1, наибольшая часть этих потерь приходится на участок полёта первой ступени. Это объясняется тем, что на этом участке траектория отклоняется от вертикали в меньшей степени, чем на участках последующих ступеней, и значение – местное ускорение гравитации и угол между вектором силы тяги двигателя и местным вектором гравитации, соответственно, являющиеся функциями времени по программе полёта. Как видно из таблицы 1, наибольшая часть этих потерь приходится на участок полёта первой ступени. Это объясняется тем, что на этом участке траектория отклоняется от вертикали в меньшей степени, чем на участках последующих ступеней, и значение 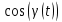 близко к максимальному значению – 1. близко к максимальному значению – 1.Аэродинамические потери вызваны сопротивлением воздушной среды при движении ракеты в ней и рассчитываются по формуле: 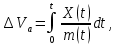 где 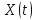 – сила лобового аэродинамического сопротивления, а – сила лобового аэродинамического сопротивления, а 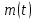 – текущая масса ракеты. Основные потери от сопротивления воздуха также приходятся на участок работы 1-й ступени ракеты Сатурн V, так как этот участок проходит в нижних, наиболее плотных слоях атмосферы. – текущая масса ракеты. Основные потери от сопротивления воздуха также приходятся на участок работы 1-й ступени ракеты Сатурн V, так как этот участок проходит в нижних, наиболее плотных слоях атмосферы.Корабль должен быть выведен на орбиту со строго определёнными параметрами. Система управления на активном участке полёта разворачивает ракету по определённой программе, при этом направление тяги двигателя отклоняется от текущего направления движения ракеты, а это влечёт за собой потери скорости на управление, которые рассчитываются по формуле: 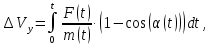 где 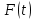 – текущая сила тяги двигателя, – текущая сила тяги двигателя, 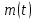 – текущая масса ракеты, а – текущая масса ракеты, а 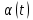 – угол между векторами тяги и скорости ракеты. Наибольшая часть потерь на управление ракеты Сатурн V приходится на участок полёта 2-й ступени, поскольку именно на этом участке происходит переход от вертикального полёта в горизонтальный (участок разворота ракеты), и вектор тяги двигателя в наибольшей степени отклоняется по направлению от вектора скорости ракеты. – угол между векторами тяги и скорости ракеты. Наибольшая часть потерь на управление ракеты Сатурн V приходится на участок полёта 2-й ступени, поскольку именно на этом участке происходит переход от вертикального полёта в горизонтальный (участок разворота ракеты), и вектор тяги двигателя в наибольшей степени отклоняется по направлению от вектора скорости ракеты.Особенности аэродинамических характеристик П 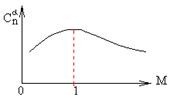 ри небольших углах атаки ( ри небольших углах атаки (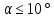 ) коэффициент продольной силы (или силы лобового сопротивления) ) коэффициент продольной силы (или силы лобового сопротивления) 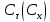 мало зависит от угла атаки, а коэффициент нормальной (подъемной) силы мало зависит от угла атаки, а коэффициент нормальной (подъемной) силы 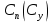 пропорционален углу атаки, т.е. пропорционален углу атаки, т.е. 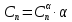 , , 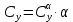 , где , где 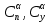 – частные производные от соответствующих коэффициентов по углу атаки. – частные производные от соответствующих коэффициентов по углу атаки.Производная 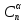 зависит главным образом от числа Маха. В области околозвуковых скоростей (число М = 1) коэффициент зависит главным образом от числа Маха. В области околозвуковых скоростей (число М = 1) коэффициент 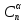 ракеты имеет максимальное значение, а в дальнейшем с увеличением числа Маха понижается, стремясь к некоторой постоянной величине. ракеты имеет максимальное значение, а в дальнейшем с увеличением числа Маха понижается, стремясь к некоторой постоянной величине.Для углов атаки до 10о ... 15о с точностью до 1...2 % расчетная зависимость для суммарного коэффициента нормальной силы имеет вид 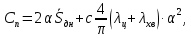 где 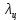 и и 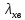 – удлинение цилиндрической и хвостовой (кормовой) части корпуса – удлинение цилиндрической и хвостовой (кормовой) части корпуса 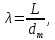 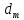 – диаметр миделевого сечения (цилиндра – для корпуса ракеты), – диаметр миделевого сечения (цилиндра – для корпуса ракеты), 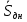 – площадь донного среза ракеты, отнесенная к площади миделя. – площадь донного среза ракеты, отнесенная к площади миделя.Величину коэффициента с при прикидочных расчетах можно выбрать, исходя из следующих условий: а) для турбулентного течения с = 0,35; б) для фюзеляжей самолетов и крупных ракетных снарядов в среднем с = 0,5 (на большей части поверхности пограничный слой турбулентный, а в передней части снаряда – ламинарный); в) при числах 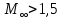 можно считать с = 1,2. можно считать с = 1,2.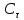 – зависит от формы ракеты, от угла атаки, от числа Маха и от числа Рейнольдса. Т.к. скорость звука а и коэффициент вязкости воздуха – зависит от формы ракеты, от угла атаки, от числа Маха и от числа Рейнольдса. Т.к. скорость звука а и коэффициент вязкости воздуха 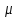 зависят от высоты полета, то при данной скорости полета ракеты V ,число Маха М и число Рейнольдса Re, а с ними зависят от высоты полета, то при данной скорости полета ракеты V ,число Маха М и число Рейнольдса Re, а с ними 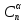 и и 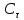 будут изменяться с высотой полета. Причем будут изменяться с высотой полета. Причем 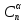 изменяется слабо, а изменяется слабо, а 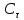 – существенно. – существенно. О 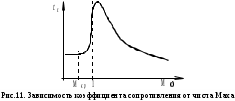 дной из составляющих силы лобового сопротивления, проявляющей себя при любых скоростях полета, является сила трения поверхности ЛА о воздушную среду. Величина коэффициента силы трения зависит от вязкости воздуха (т.е. от высоты полета) и скорости движения ЛА. Причем характер влияния их на дной из составляющих силы лобового сопротивления, проявляющей себя при любых скоростях полета, является сила трения поверхности ЛА о воздушную среду. Величина коэффициента силы трения зависит от вязкости воздуха (т.е. от высоты полета) и скорости движения ЛА. Причем характер влияния их на 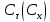 противоположен: чем больше скорость движения (число Маха), тем меньше величина коэффициента сопротивления трения и наоборот – чем больше высота полета, тем больше противоположен: чем больше скорость движения (число Маха), тем меньше величина коэффициента сопротивления трения и наоборот – чем больше высота полета, тем больше 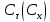 . Другой составляющей . Другой составляющей 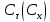 при сверхзвуковых скоростях полета (М > 1) является коэффициент волнового сопротивления, величина которого с ростом числа Маха быстро уменьшается. Характерная зависимость суммарного коэффициента сопротивления от числа Маха приведена на рис. 11. Как видно, наибольшая величина при сверхзвуковых скоростях полета (М > 1) является коэффициент волнового сопротивления, величина которого с ростом числа Маха быстро уменьшается. Характерная зависимость суммарного коэффициента сопротивления от числа Маха приведена на рис. 11. Как видно, наибольшая величина 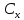 соответствует околозвуковому диапазону скоростей. Горб сопротивления обусловлен волновым сопротивлением, максимум которого приходится на этот, переходный диапазон околозвуковых скоростей соответствует околозвуковому диапазону скоростей. Горб сопротивления обусловлен волновым сопротивлением, максимум которого приходится на этот, переходный диапазон околозвуковых скоростей Подводя итог можно сказать: действующие аэродинамические силы зависят от формы и размеров ракеты, от угла атаки 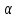 , от высоты h и скорости полета ракеты V. , от высоты h и скорости полета ракеты V.Аэродинамические моменты И  звестно, что аэродинамические силы, действующие на ракету, можно свести к одной результирующей силе RA. Точка, лежащая на продольной оси ракеты, через которую проходит линия действия результирующей аэродинамической силы, носит название центр давления. звестно, что аэродинамические силы, действующие на ракету, можно свести к одной результирующей силе RA. Точка, лежащая на продольной оси ракеты, через которую проходит линия действия результирующей аэродинамической силы, носит название центр давления.Д Рис.12 ля удобства анализа действия сил, приложенных к ракете, рассмотрим плоскую задачу, т.е. при β = 0. При составлении уравнения движения ракеты исходим из того, что все силы, действующие на ракету, приложены к центру тяжести (центру масс) ракеты (рис.12). Тогда полный аэродинамический момент равен 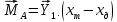 . В проекциях на оси связанной системы координат: . В проекциях на оси связанной системы координат: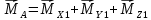 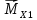 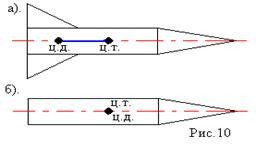 – момент крена; – момент крена;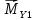 – момент рысканья; – момент рысканья;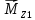 – момент тангажа. – момент тангажа.Величина и направление 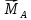 зависит от ряда факторов: зависит от ряда факторов:– от положения центра давления; – от скорости движения ракеты; – Рис.13 от угловой скорости вращения ракеты. Положение центра давления в общем случае зависит от формы ракеты, числа Маха и от угла атаки. Если ракета не имеет стабилизаторов (рис.13б), то центр давления находится в центре тяжести (ориентировочно, в первом приближении). В схеме со стабилизаторами (рис.13а) центр давления смещается к хвостовой части. В первом приближении можно считать, что положение центра давления остается постоянным, если угол атаки α изменяется в некоторой малой окрестности своего нулевого значения. Коэффициент центра давления длинных тел Рассмотрим расчетную схему нахождения положения центра давления тела вращения, состоящего из нескольких отсеков разного типа. Расчленим это тело на такие элементы, для каждого из которых известны создаваемая им нормальная сила и точка ее приложения (рис.14). Для конических головных частей центр давления расположен на расстоянии 2/3 высоты от вершины конуса. Считаем, что цилиндрическая часть вся в равной мере создает нормальную силу, и точка ее приложения лежит в центре цилиндра. Поскольку хвостовые нецилиндрические отсеки имеют малые углы конусности, то в первом приближении можно считать, что и для них центр давления расположен в геометрическом центре отсека. Т 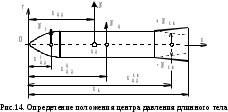 огда суммарная нормальная сила для всего корпуса тела вращения, изображенного на рис.14, равна огда суммарная нормальная сила для всего корпуса тела вращения, изображенного на рис.14, равна 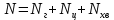 , где , где 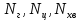 – нормальные силы, создаваемые головной, цилиндрической и хвостовой частями. Вычислим сумму моментов всех сил относительно носка тела вращения (точки О): – нормальные силы, создаваемые головной, цилиндрической и хвостовой частями. Вычислим сумму моментов всех сил относительно носка тела вращения (точки О):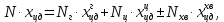 где 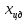 , , 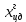 , … – координаты центров давления указанных частей корпуса ЛА. Знак «+» составляющей момента от , … – координаты центров давления указанных частей корпуса ЛА. Знак «+» составляющей момента от 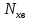 соответствует расширяющейся, а «-» – сужающейся хвостовой части. соответствует расширяющейся, а «-» – сужающейся хвостовой части.Переходя к коэффициентам сил и относительным координатам, имеем: 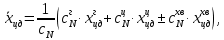 где 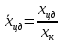 , а коэффициенты , а коэффициенты 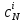 нормальных сил определяются обычным образом. нормальных сил определяются обычным образом.Демпфирующий момент При вращательном движении ракеты в воздушной среде, сопротивление воздушной среды вращению проявляется в виде аэродинамического момента, который называют демпфирующим моментом. Демпфирующий момент всегда направлен в сторону противоположную вращению и стремится погасить угловую скорость вращения. Величина момента зависит от угловой скорости вращения и от ее ориентации относительно ракеты. Полный демпфирующий момент можно разложить на три составляющие по осям OX1, OY1, OZ1. 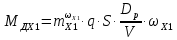 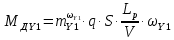 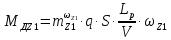 Здесь Dp – диаметр ракеты, Lp – длина ракеты, V – скорость движения ракеты, q – cкоростной напор, S – площадь миделя ракеты, 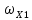 , , 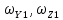 – проекции угловой скорости ракеты относительно осей связанной системы координат, – проекции угловой скорости ракеты относительно осей связанной системы координат, 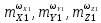 – коэффициенты моментов относительно этих осей (всегда отрицательные), их величины зависят от формы ракеты, от положения центра тяжести и от числа Маха. – коэффициенты моментов относительно этих осей (всегда отрицательные), их величины зависят от формы ракеты, от положения центра тяжести и от числа Маха.Управляющие силы и моменты Известно, что общее движение ракеты или ЛА можно разделить на движение центра масс и движение ЛА вокруг собственного центра масс. Поэтому задачу управления полетом ЛА можно разделить на две части: – управление движением центра масс, т.е. изменение величины и направления вектора скорости; – управление вращательным движением относительно центра масс. В общем случае в полете на ракету действуют следующие силы: G – вес ракеты; RA – полная аэродинамическая сила; Р – сила тяги. Примечание: При старте на ракету могут действовать силы реакции стартовых устройств. Для изменения траектории полета нужно изменить величину и направление равнодействующей всех этих трех сил. Т.к. на силу тяжести влиять невозможно, то управлять полетом можно лишь изменяя величину и направление RA и Р (рис. 15). Заменим эти две силы равнодействующей: 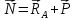 . Разложим ее на нормальную и касательную составляющие к траектории движения ЛА: . Разложим ее на нормальную и касательную составляющие к траектории движения ЛА: 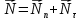 . .В проекции на касательную к траектории движения ЛА: 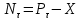 . .Изменение 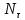 достигается (и в баллистических расчетах также) изменением тяги маршевых двигателей. Для баллистических ракет с ЖРД изменение силы тяги происходит за счет изменения секундного расхода топлива. достигается (и в баллистических расчетах также) изменением тяги маршевых двигателей. Для баллистических ракет с ЖРД изменение силы тяги происходит за счет изменения секундного расхода топлива.Ту часть силы 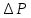 , которую можно использовать для регулирования скорости ракеты принято называть тангенциальной управляющей силой. Нормальная составляющая управляющей силы обеспечивает управление положением ЛА в пространстве (рис. 16). , которую можно использовать для регулирования скорости ракеты принято называть тангенциальной управляющей силой. Нормальная составляющая управляющей силы обеспечивает управление положением ЛА в пространстве (рис. 16).Рассмотрим 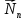 : : 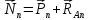 так как так как 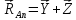 , то , то 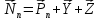 . В проекциях на оси координат . В проекциях на оси координат 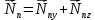 , где , где  – нормальная управляющая сила, а – нормальная управляющая сила, а  – боковая управляющая сила. – боковая управляющая сила.С  Рис.15 Рис.16 оздавая необходимые по величине и направлению тангенциальную, нормальную и боковую управляющие силы можно обеспечить заданную траекторию полета ракеты. |