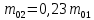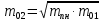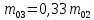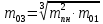механика полёта. Механика полета. Механика
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Возмущающие силы и моменты В реальном полете на реальную ракету всегда действуют возмущающие силы и моменты, вызванные различными факторами. К ним относят: а) отклонение параметров ракеты и ее двигателей (вес ракеты, сила тяги основных двигателей, секундный расход топлива и т.д.) от номинальных значений. Это отклонение вызвано главным образом производственными потребностями при сборке агрегатов ракеты, а также разбросом характеристик ракетного топлива; б) эксцентриситет тяги основного ракетного двигателя; в) несимметричность ракеты; г) атмосферные возмущения. Атмосферные возмущения Отклонение параметров реальной атмосферы от стандартных значений приводит к появлению возмущающих аэродинамических сил и моментов, а также к отклонению вектора тяги от номинальной величины (рн). Ветровое воздействие атмосферы на ракету вызывает появление возмущающих аэродинамических сил и моментов. Атмосферные возмущения представляют собой случайные процессы и должны описываться в уравнениях движения случайными функциями. При составлении уравнений движений ракеты, а также при его исследовании невозможно учесть все возмущающие факторы, действующие на ракету. В зависимости от конкретных условий постоянной задачи необходимо учитывать те из них , которые существенно влияют на решение задачи. Возмущающие факторы, воздействующие непосредственно на ракету и на процессы управления полетом в конечном итоге приводят к уменьшению дальности полета к рассеиванию точек попадания ГЧ (для УБР). Расчет траектории управляемых баллистических ракет (УБР) Общий вид траектории УБР и параметры активного участка Участки полета (траектории) (рис. 34): ОА – активный участок полета (активный участок траектории – АУТ) – участок полёта летательного аппарата, на котором работает маршевый двигатель ЛА. Величина и направление скорости в конце активного участка 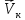 определяются заданной дальностью стрельбы (полета ЛА). Активный участок траектории подразделяется на три более мелких участка: стартовый, программного разворота и наведения (или доведения). определяются заданной дальностью стрельбы (полета ЛА). Активный участок траектории подразделяется на три более мелких участка: стартовый, программного разворота и наведения (или доведения).М 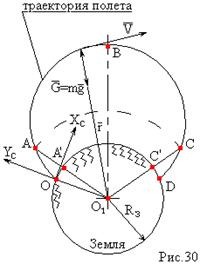 омент выключения двигателя разделяет траекторию движения ракеты на активный и пассивный участки. В момент выключения двигателя управление ракетой заканчивается и для БР происходит отделение головной части. омент выключения двигателя разделяет траекторию движения ракеты на активный и пассивный участки. В момент выключения двигателя управление ракетой заканчивается и для БР происходит отделение головной части.Пассивным участком полёта (траектории) АВD, в противоположность активному, называется участок, на котором маршевый двигатель ЛА не работает и аппарат движется по инерции за счет запаса кинетической (скорость) и потенциальной (высота полета) энергии, приобретенного на активном участке траектории. Ракета совершает движение по баллистической кривой. Н 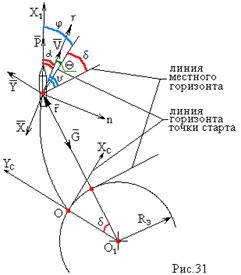 Рис.34 а пассивном (эллиптическом) участке траектории на ракету вне атмосферы действует только силы гравитации (сила тяжести G). На пассивном атмосферном участке траектории на ЛА (ракета, ГЧ или спускаемый аппарат) действуют и сила тяжести, и сила аэродинамического сопротивления. Б Рис.35 аллистическая траектория и точка ее пересечения с поверхностью Земли (D) зависят от координат ракеты, величины и направления ее скорости в момент выключения двигателя (конечные параметры). То есть задача управления баллистическими ракетами состоит в том, чтобы к моменту выключения двигателя ракета была выведена в расчетную точку пространства (Xк, Yк) и имела при этом расчетную по величине и направлению скорость движения. Если эти условия не соблюсти, то ошибка уже не может быть исправлена (ракета не попадет в цель), так как на пассивном участке траектории ракета не управляется. Параметры активного участка траектории УБР (рис. 35) φ – угол тангажа – угол между продольной осью ракеты и линией горизонта точки старта. Θ – угол траектории (угол наклона траектории к горизонту) – угол между вектором скорости и линией горизонта точки старта в плоскости стрельбы. υ – угол траектории относительно местного горизонта – угол между вектором скорости и линией местного горизонта. δ – полярный угол, характеризует наклонение плоскости местного горизонта к плоскости точки старта. α – угол атаки – угол между вектором скорости и продольной осью ракеты (для плоской задачи). Требования к траектории 1. Программа полета должна обеспечивать минимум рассеивания траектории в конце АУТ. В связи с этим угол траектории Θ в конце АУТ должен быть оптимальным. Анализ траектории показывает, что значение оптимального угла Θ может определяться: – с точки зрения максимальной дальности полета; – с точки зрения минимального рассеивания точек попадания. Известно, что эти значения угла Θ не совпадают между собой. Будем учитывать оптимальное значение угла Θ, полученное из условий максимальной дальности полета. При сравнительно малых дальностях (100 … 300 км) угол тангажа 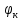 в момент выключения двигателя близок к 45°. При больших дальностях он уменьшается и может быть равным 17° … 25°. в момент выключения двигателя близок к 45°. При больших дальностях он уменьшается и может быть равным 17° … 25°. 2. Стартовый участок тяжелых (баллистических) ракет – вертикальный, а время движения на вертикальном участке невелико. Причины использования вертикального старта: – обеспечение устойчивости движения ракеты в начале полета при малых скоростях; – ракета проходит наиболее плотные слои атмосферы по кратчайшему расстоянию, с относительно небольшой скоростью и при нулевых углах атаки (это сводит к минимуму аэродинамическое сопротивление и нагрев ракеты); – при вертикальном старте конструкция ракеты испытывает в основном осевые перегрузки, поэтому конструкция может не иметь большую поперечную жесткость (уменьшается стартовая масса ракеты); – удобство старта ракеты с горизонтального стола пускового устройства (упрощается проектирование и изготовление пускового устройства, которое удерживает ракету перед стартом сь помощью одних только хвостовых опор). 3. Траектория движения ракеты на АУТ не должна иметь резких перегибов. Математически это означает, что должны быть наложены ограничения на первую и вторую производные от угла траектории Θ. Известно, что 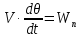 . .Здесь 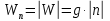 – нормальное ускорение, где – нормальное ускорение, где 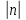 – коэффициент перегрузки. – коэффициент перегрузки.Таким образом, первая производная определяет нормальное ускорение Wn и позволяет определить силу, действующую на корпус ракеты при маневрах. 4. При выводе уравнений движения баллистических ракет предполагается, что ракета является абсолютно жестким телом, т.е. не учитывают упругость корпуса ракеты и наличие жидкости в баках. Использование формулы Циолковского при проектировании ракет Выведенная в конце XIХ века, формула Циолковского и сегодня составляет важную часть математического аппарата, используемого при проектировании ракет, в частности, при определении их основных массовых характеристик. Путём несложных преобразований формулы получаем следующее уравнение: 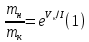 Это уравнение дает отношение начальной массы ракеты к её конечной массе при заданных значениях конечной скорости ракеты и удельного импульса. Введём следующие обозначения: 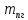 – масса полезного груза; – масса полезного груза;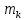 – масса конструкции ракеты; – масса конструкции ракеты;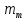 – масса топлива. – масса топлива.Масса конструкции ракеты в большом диапазоне значений зависит от массы топлива почти линейно: чем больше запас топлива, тем больше размеры и масса ёмкостей для его хранения, больше масса несущих элементов конструкции, мощнее (следовательно, массивнее) двигательная установка. Выразим эту зависимость в виде: 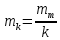 Где k – коэффициент, показывающий, какое количество топлива приходится на единицу массы конструкции (коэффициент конструктивного совершенства). При рациональном конструировании этот коэффициент в первую очередь зависит от характеристик (плотности и прочности) конструкционных материалов, используемых в производстве ракеты. Чем прочнее и легче используемые материалы, тем выше значение коэффициента k. Этот коэффициент зависит также от усреднённой плотности топлива (для менее плотного топлива требуются ёмкости большего размера и массы, что ведёт к снижению значения k). Конструктивное совершенство определяется общим уровнем развития техники на данном этапе развития техники. Так, например, для различных блоков РН "Сатурн-V" k = 0,061...0,127. Уравнение (1) может быть записано в виде: 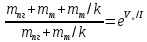 , ,что путём элементарных преобразований приводится к виду: 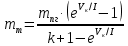 (3) (3)Эта форма уравнения Циолковского позволяет рассчитать массу топлива, необходимого для достижения одноступенчатой ракетой заданной характеристической скорости, при заданной массе полезного груза, значении удельного импульса и значении коэффициента k. Разумеется, эта формула имеет смысл, только когда значение, получающееся при подстановке исходных данных, положительно. Поскольку экспонента для положительного аргумента всегда больше 1, числитель формулы всегда положителен, следовательно, положительным должен быть и знаменатель этой формулы: 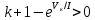 , иначе говоря, , иначе говоря, 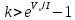 (4) (4)Это неравенство является критерием достижимости одноступенчатой ракетой заданной скорости 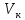 при заданных значениях удельного импульса Iи коэффициента k. Если неравенство не выполняется, то заданная скорость не может быть достигнута ни при каких затратах топлива: с увеличением количества топлива будет возрастать и масса конструкции ракеты и отношение начальной массы ракеты к конечной никогда не достигнет значения, требуемого формулой Циолковского для достижения заданной скорости. при заданных значениях удельного импульса Iи коэффициента k. Если неравенство не выполняется, то заданная скорость не может быть достигнута ни при каких затратах топлива: с увеличением количества топлива будет возрастать и масса конструкции ракеты и отношение начальной массы ракеты к конечной никогда не достигнет значения, требуемого формулой Циолковского для достижения заданной скорости.Пример расчёта массы ракеты Требуется вывести искусственный спутник Земли массой 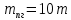 на круговую орбиту высотой 250 км. Располагаемый двигатель имеет удельный импульс на круговую орбиту высотой 250 км. Располагаемый двигатель имеет удельный импульс 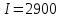 м/c. Коэффициент м/c. Коэффициент 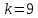 – это значит, что масса конструкции составляет 10 % от массы заправленной ракеты (ступени). Определим массу ракеты-носителя. – это значит, что масса конструкции составляет 10 % от массы заправленной ракеты (ступени). Определим массу ракеты-носителя.Первая космическая скорость для выбранной орбиты составляет 7759,4 м/с, к которой добавляются предполагаемые потери от гравитации 600 м/c (это, как можно видеть, меньше, чем потери, приведённые в таблице 1, но и орбита, которую предстоит достичь – вдвое ниже). Характеристическая скорость, таким образом, равна 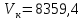 м/c (остальными потерями в первом приближении можно пренебречь). При таких параметрах величина м/c (остальными потерями в первом приближении можно пренебречь). При таких параметрах величина 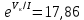 . Неравенство (4), очевидно, не выполняется, следовательно, одноступенчатой ракетой при данных условиях достижение поставленной цели невозможно. . Неравенство (4), очевидно, не выполняется, следовательно, одноступенчатой ракетой при данных условиях достижение поставленной цели невозможно.Расчёт для двухступенчатой ракеты. Разделим пополам характеристическую скорость, что составит характеристическую скорость для каждой из ступеней двухступенчатой ракеты 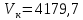 м/c. На этот раз м/c. На этот раз 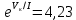 , что удовлетворяет критерию достижимости (4), и, подставляя в формулы (3) и (2) значения, , что удовлетворяет критерию достижимости (4), и, подставляя в формулы (3) и (2) значения,для 2-й ступени получаем: 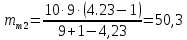 т; т;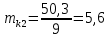 т; т;полная масса 2-й ступени составляет 55,9 т. Для 1-й ступени к массе полезной нагрузки добавляется полная масса 2-й ступени, и после соответствующей подстановки получаем: 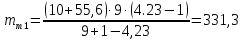 т; т;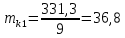 т; т;полная масса 1-й ступени составляет 368,1 т; общая масса двухступенчатой ракеты с полезным грузом составит 10 + 55,9 + 368,1 = 434 т. Аналогичным образом выполняются расчёты для большего количества ступеней. В результате получаем: Стартовая масса трёхступенчатой ракеты составит 323,1 т. Четырёхступенчатой – 294,2 т. Пятиступенчатой – 281 т. На этом примере видно, как оправдывается многоступенчатость в ракетостроении: при той же конечной скорости ракета с большим числом ступеней имеет меньшую массу. Следует отметить, что эти результаты получены в предположении, что коэффициент конструктивного совершенства ракеты 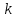 остаётся постоянным, независимо от количества ступеней. Более тщательное рассмотрение показывает, что это – сильное упрощение. Ступени соединяются между собой специальными секциями – переходниками – несущими конструкциями. Каждая из них должна выдерживать суммарный вес всех последующих ступеней, помноженный на максимальное значение перегрузки, которую испытывает ракета на всех участках полёта, на которых переходник входит в состав ракеты. С увеличением числа ступеней их суммарная масса уменьшается, в то время как количество и суммарная масса переходников возрастают, что ведёт к снижению коэффициента остаётся постоянным, независимо от количества ступеней. Более тщательное рассмотрение показывает, что это – сильное упрощение. Ступени соединяются между собой специальными секциями – переходниками – несущими конструкциями. Каждая из них должна выдерживать суммарный вес всех последующих ступеней, помноженный на максимальное значение перегрузки, которую испытывает ракета на всех участках полёта, на которых переходник входит в состав ракеты. С увеличением числа ступеней их суммарная масса уменьшается, в то время как количество и суммарная масса переходников возрастают, что ведёт к снижению коэффициента 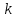 , а, вместе с ним, и положительного эффекта многоступенчатости. В современной практике ракетостроения более четырёх ступеней, как правило, не делается. , а, вместе с ним, и положительного эффекта многоступенчатости. В современной практике ракетостроения более четырёх ступеней, как правило, не делается.Анализ баллистических возможностей ракет говорит о следующем: Примерно одинаковую массу при массе полезной нагрузки 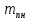 = 500 … 1000 кг имеют: = 500 … 1000 кг имеют:одноступенчатые ракеты с ЖРД и двухступенчатые с РДТТ в диапазоне максимальных дальностей полета 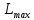 = 1000 … 4000 км; = 1000 … 4000 км;двухступенчатые ракеты с ЖРД и трехступенчатые ракеты с РДТТ в диапазоне 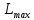 = 4000 … 10000 км. = 4000 … 10000 км.При дальностях 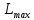 = 4000 … 10000 км у ракет с ЖРД оптимальное число ступеней близко к двум-трем, а для ракет с РДТТ – к трем-четырем. = 4000 … 10000 км у ракет с ЖРД оптимальное число ступеней близко к двум-трем, а для ракет с РДТТ – к трем-четырем.При этом приращения скорости, сообщаемые ступенями для двух- и трехступенчатых ракет, имеют различные пропорции (табл. 2). Оптимальное соотношение масс ступеней зависит от коэффициента тяговооруженности, представляющего собой отношение тяги двигателя к начальной массе ракеты. Поэтому для анализа влияния различных параметров ракеты на оптимальное соотношение масс ступеней обычно рассматривают скорость полета, определяемую с учетом величины коэффициента тяговооруженности. При баллистическом проектировании в качестве предварительных можно принимать соотношения масс ступеней, как в табл. 3. Такого рода расчёты выполняются не только на первом этапе проектирования – при выборе варианта компоновки ракеты, но и на последующих стадиях проектирования, по мере детализации конструкции. Формула Циолковского постоянно используется при поверочных расчётах, когда характеристические скорости пересчитываются, с учётом сложившихся из конкретных деталей соотношений начальной и конечной массы ракеты (ступени), конкретных характеристик двигательной установки, уточнения потерь скорости после расчёта программы полёта на активном участке, и т.д., с целью контроля достижения ракетой заданной скорости. Таблица 2 Приращение скорости ракеты
Таблица 3 Соотношение масс ступеней ракеты
Элементы небесной механики Небесная механика – раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается предвычислением положения Луны и планет, предсказанием места и времени затмений, в общем, определением реального движения космических тел. Естественно, что небесная механика в первую очередь изучает поведение тел Солнечной системы (обращение планет вокруг Солнца, спутников вокруг планет, движение комет и других малых небесных тел). Тогда как перемещение далеких звёзд удается заметить, в лучшем случае, за десятилетия и века, движение членов Солнечной системы происходит буквально на глазах – за дни, часы и даже минуты. Поэтому его изучение стало началом современной небесной механики, рождённой трудами И. Кеплера (1571—1630) и И. Ньютона (1643—1727). Кеплер впервые установил законы планетного движения. Законы Кеплера Законы Кеплера – это три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. В рамках классической механики выводятся из решения задачи двух тел предельным переходом 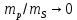 , где , где 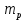 , , 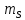 – массы планеты и Солнца соответственно. – массы планеты и Солнца соответственно.П  ервый закон Кеплера (закон эллипсов) ервый закон Кеплера (закон эллипсов)Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 36). Ф Рис.36 орма эллипса и степень его сходства с окружностью характеризуется отношением 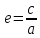 , где , где 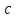 – расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a – большая полуось. Величина – расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a – большая полуось. Величина 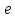 называется эксцентриситетом эллипса. При называется эксцентриситетом эллипса. При 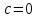 , и, следовательно, , и, следовательно, 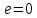 эллипс превращается в окружность. эллипс превращается в окружность.В 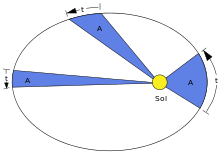 торой закон Кеплера (закон площадей). торой закон Кеплера (закон площадей).Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади (рис.37). П Рис.37 рименительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий – ближайшая к Солнцу точка орбиты, и афелий – наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу. Третий закон Кеплера (гармонический закон) Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет (это соотношение справедливо не только для планет, но и для их спутников): 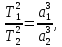 Где 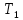 и и 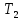 – периоды обращения двух планет вокруг Солнца, а – периоды обращения двух планет вокруг Солнца, а 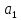 и и 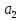 – длины больших полуосей их орбит. – длины больших полуосей их орбит.Ньютон вывел из законов Кеплера закон всемирного тяготения и использовал законы движения и тяготения для решения небесно-механических проблем, не охваченных законами Кеплера. После Ньютона прогресс в небесной механике в основном заключался в развитии математической техники для решения уравнений, выражающих законы Ньютона. Таким образом, принципы небесной механики – это «классика» в том смысле, что и сегодня они такие же, как во времена Ньютона. Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен – в действительности в него входит и масса планеты: 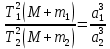 , где , где 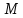 – масса Солнца, а – масса Солнца, а 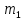 и и 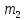 – массы планет. – массы планет.Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды. Применение результатов небесной механики к движению искусственных спутников и космических кораблей составляет астродинамику Астродинамика – раздел небесной механики, изучающий движение искусственных космических тел: искусственных спутников, межпланетных станций и других космических кораблей. В сферу задач астродинамики входят расчёт орбит космических кораблей, определение параметров их запуска, вычисление изменений орбит в результате манёвров, планирование гравитационных манёвров и другие практические задачи. Результаты астродинамики используются при планировании и проведении любых космических миссий. Астродинамика выделяется из небесной механики, которая изучает в первую очередь движение естественных космических тел под действием сил тяготения, своей ориентированностью на решение прикладных задач управления космическими кораблями. В связи с этим в астродинамике требуется учитывать и факторы, игнорируемые классической небесной механикой – влияние атмосферы и магнитного поля Земли, гравитационных аномалий, давления солнечного излучения и другие. Орбита (от лат. Orbita — колея, дорога, путь) – траектория движения материальной точки в наперёд заданной системе пространственных координат для заданной в этих координатах конфигурации поля сил, которые на неё действуют. В небесной механике это траектория небесного тела в гравитационном поле другого тела, обладающего значительно большей массой (планеты, кометы, астероида в поле звезды). В прямоугольной системе координат, начало которой совпадает с центром масс, траектория может иметь форму конического сечения (окружности, эллипса, параболы или гиперболы). При этом его фокус совпадает с центром масс системы. Д 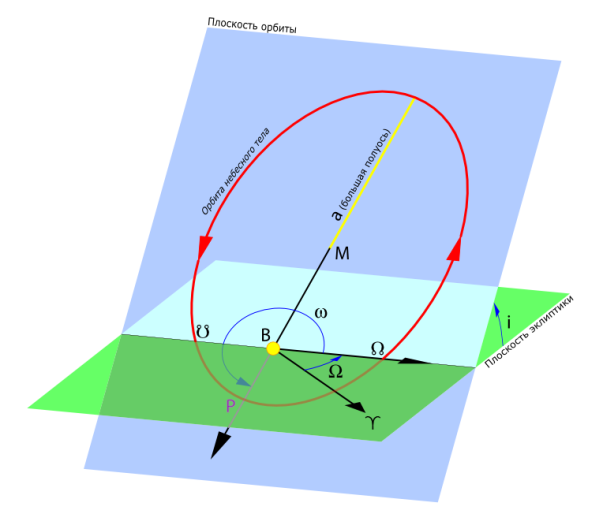 олгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона, описывающих орбитальное движение тел. олгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона, описывающих орбитальное движение тел.Кеплеровыми элементами орбиты являются (рис. 38): фокальный параметр5 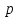 , большая полуось , большая полуось 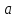 , радиус перицентра и радиус апоцентра6 — определяют размер орбиты, , радиус перицентра и радиус апоцентра6 — определяют размер орбиты,эксцентриситет (e)— определяет форму орбиты, наклонение орбиты (i), долгота восходящего узла (Ω) – определяет положение плоскости орбиты небесного тела в пространстве, а Рис.38 ргумент перицентра (ω) – задаёт ориентацию аппарата в плоскости орбиты (часто задают направление на перицентр), момент прохождения небесного тела через перицентр ( 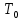 ) – задаёт привязку по времени. ) – задаёт привязку по времени.Эти элементы однозначно определяют орбиту независимо от её формы (эллиптической, параболической или гиперболической). Основной координатной плоскостью может быть плоскость эклиптики, плоскость галактики, плоскость земного экватора и т. д. Тогда элементы орбиты задаются относительно выбранной плоскости. По геометрической форме орбиты делятся на круговые и эллиптические, с тем или иным эксцентриситетом. Также существует разделение на замкнутые и незамкнутые орбиты, в особенности для КЛА. По углу наклонения i плоскости орбиты к плоскости земного экватора – на экваториальные (i = 0°), полярные (i = 90°) и наклонные (i – любое, кроме 0° и 90°). По соотношению периода обращения Тоб вокруг земного шара с земными или солнечными сутками – на не синхронные, квазисинхронные, синхронно-суточные (геосинхронные), солнечно-синхронные. Орбитальная скорость тела (планеты, естественного или искусственного спутника, звезды) – это скорость, с которой оно вращается вокруг барицентра системы, как правило, вокруг более массивного тела (табл. 4). Таблица 4 Орбитальные скорости планет солнечной системы
Орбиты космических аппаратов вокруг Земли
Низкая опорная орбита (НОО, низкая околоземная орбита) – орбита космического аппарата около Земли. Орбиту правомерно называть «опорной», если предполагается её изменение – увеличение высоты или изменение наклонения. Если же маневры не предусмотрены или космический аппарат вообще не имеет собственной двигательной установки, предпочтительно использование названия «низкая околоземная орбита». В общем случае считается, что космический аппарат находится на опорной орбите, если он движется с первой космической скоростью, и находится на высоте, где соответствующая плотность верхних слоёв атмосферы, в первом приближении, допускает круговое или эллиптическое движение. При этом на орбите такого типа аппарат может находиться не менее одного витка. Типичные параметры опорной орбиты, на примере космического корабля «Союз-ТМА» составляют: минимальная высота над уровнем моря (в перигее) – 193 км, максимальная высота над уровнем моря (в апогее) – 220 км, наклонение – 51,6 градуса, период обращения – около 88,3 минуты. При определении высоты НОО важно указывать, от какой модели Земли она отсчитывается. Российские баллистики традиционно указывают высоту над эллипсоидом, а американские – над сферой, в результате разница может достигать 20 км (примерно соответствует разнице экваториального и полярного радиусов Земли), а положения апогея и перигея – смещаться. Так как суточное вращение Земли участвует в выведении ракеты-носителя на орбиту, то грузоподъёмность зависит от наклонения орбиты к плоскости экватора. Наилучшие условия достигаются, если НОО имеет наклон к экватору, который совпадает с широтой стартовой площадки, с которой был осуществлён запуск. Другие наклонения орбиты ведут к уменьшению параметров ракеты-носителя по способности вывода груза на орбиту. Однако, не для всех космодромов возможен запуск в наиболее энергетически выгодном направлении, так, например, для Байконура с широтой около 46 градусов невозможен запуск на наклонения меньше 48,5 градусов из-за ограничений по расположению территорий падения отделяющихся частей ракет (зон отчуждения). Наиболее часто используемое наклонение при запусках с Байконура – 51,6 градуса, меньшие наклонения используются редко. Время жизни, или время нахождения КА на НОО, зависят от баллистических параметров искусственного небесного тела и от активности Солнца в этот период, которая влияет на высоту верхних слоёв атмосферы Земли. Чем ниже орбита, тем больше масса груза, который может вывести на неё ракета-носитель при прочих равных условиях. Поэтому опорную орбиту выгодно делать как можно ниже. На практике время орбитального полёта (до вхождения в плотные слои атмосферы) менее одних суток может вызвать проблемы при отказах на борту космического аппарата, поэтому такие низкие орбиты практически не используются. Кроме того, на минимальную высоту опорной орбиты влияет величина погрешности выведения, так как при неблагоприятном сочетании ошибок измерительных приборов, органов управления и внешних факторов орбита может оказаться слишком низкой и КА вернётся в атмосферу Земли и сгорит, прежде чем успеет сманеврировать. Тем не менее, известны случаи выведения аппаратов на орбиты с периодом обращения менее 88 минут и высотой перигея 121—150 км. Например, на опорную орбиту с перигеем 129 км была выведена автоматическая станция Луна-7. Понятие «опорная орбита» вошло в обиход с началом запусков четырёхступенчатой ракеты 8К78 «Молния», четвёртая ступень которой запускалась в невесомости после совершения примерно 3/4 оборота вокруг Земли, как требовалось для межпланетных и лунных АМС. Низкая околоземная орбита может использоваться не только как опорная, но и как рабочая. В общем случае низкими считаются орбиты с высотой апогея до 2000 км. Особой разновидностью низких околоземных орбит является солнечно-синхронная орбита. На такие орбиты запускаются спутники дистанционного зондирования Земли. На низкой околоземной орбите находится МКС. После завершения в 1972 году программы «Аполлон» все пилотируемые полёты в космосе происходят по низкой околоземной орбите. В связи с интенсивным использованием на низких орбитах обращается большое количество космического мусора, что приводит к осложнениям в эксплуатации МКС. Время нахождения спутника на НОО зависит от многих факторов, особенно сильно зависит от влияния Луны и высоты над плотными слоями атмосферы. Например, орбита ИСЗ «Эксплорер-6» (США) менялась каждые 3 месяца от 250 до 160 км, что привело к сроку службы спутника в 2 года вместо 20 запланированных, также первый спутник Земли просуществовал 3 месяца (перигей 215 км, апогей 939 км). Возросшая солнечная активность может привести к резкому увеличению плотности верхней атмосферы – в результате спутник тормозится сильнее, а высота его орбиты снижается быстрее. Существенную роль играет и форма спутника, а именно площадь его миделя (поперечного сечения); для спутников, специально предназначенных к работе на низких орбитах, зачастую выбирают стреловидную, аэродинамически обтекаемую форму корпуса. Солнечно-синхронная орбита (иногда именуемая гелиосинхронной) – геоцентрическая орбита с такими параметрами, что объект, находящийся на ней, проходит над любой точкой земной поверхности приблизительно в одно и то же местное солнечное время. Таким образом, угол освещения земной поверхности будет приблизительно одинаковым на всех проходах спутника. Такие постоянные условия освещения очень хорошо подходят для спутников, получающих изображения земной поверхности (в том числе спутников дистанционного зондирования земли, метеоспутников). Однако присутствуют годовые колебания солнечного времени, вызванные эллиптичностью земной орбиты. Например, спутник LandSat-7, находящийся на солнечно-синхронной орбите, может пересекать экватор пятнадцать раз в сутки, каждый раз в 10:00 местного времени. Для достижения подобных характеристик параметры орбиты выбираются таким образом, чтобы орбита прецессировала в восточном направлении на 360 градусов в год (приблизительно на 1 градус в день), компенсируя вращение Земли вокруг Солнца. Прецессия происходит за счёт взаимодействия спутника с Землёй, несферичной из-за полярного сжатия. Скорость прецессии зависит от наклонения орбиты. Нужной скорости прецессии можно достичь лишь для определённого диапазона высот орбит (как правило, выбираются значения 600—800 км, с периодами 96—100 мин.), необходимое наклонение для упомянутого диапазона высот около 98°. Для орбит с бо́льшими высотами требуются весьма большие значения наклонения, из-за чего в зону посещений спутника перестают попадать полярные области. Данный тип орбит может иметь различные вариации. Например, возможны солнечно-синхронные орбиты с большим эксцентриситетом. В этом случае солнечное время прохода будет зафиксировано только для одной точки орбиты (как правило, перигея). Период обращения выбирается в соответствии с необходимым периодом повторных проходов над одной и той же точкой поверхности. Хотя спутник на круговой солнечно-синхронной орбите пересекает экватор в одно и то же местное время, это происходит в разных точках экватора (на разной долготе) из-за того, что Земля поворачивается на некоторый угол между проходами спутника. Предположим, период обращения составляет 96 мин. Это значение нацело делит солнечные сутки7 на пятнадцать. Таким образом, за сутки спутник пройдёт над пятнадцатью разными точками экватора на дневной стороне орбиты (и еще над пятнадцатью — на ночной) и вернется к первой точке. Подбором более сложных (нецелых) отношений, число посещаемых точек может быть увеличено за счёт увеличения периода посещения одной и той же точки. Специальным случаем солнечно-синхронной орбиты является орбита, на которой посещение экватора происходит в полдень/полночь, а также орбита, лежащая в плоскости терминатора8, то есть в полосе закатов и восходов. Последний вариант не имеет смысла для спутников, осуществляющих оптическую фотосъёмку, но хорош для радарных спутников, так как обеспечивает отсутствие участков орбиты, на которых спутник попадает в тень Земли. Таким образом, на такой орбите солнечные батареи спутника постоянно освещаются Солнцем. Геоцентрическая орбита – траектория движения небесного тела по эллиптической траектории вокруг Земли. Один из двух фокусов эллипса, по которому движется небесное тело, совпадает с Землёй. Для того, чтобы космический корабль оказался на этой орбите, ему необходимо сообщить скорость, которая меньше второй космической скорости, но не меньше чем первая космическая скорость. Высокая эллиптическая орбита (ВЭО) – это тип эллиптической орбиты, у которой высота в апогее во много раз превышает высоту в перигее. По законам Кеплера спутники, использующие высокие эллиптические орбиты, двигаются с очень высокой скоростью в перигее, а затем сильно замедляются в апогее. Когда КА находится близко от апогея, у наземного наблюдателя создаётся впечатление, что спутник почти не двигается в течение нескольких часов, то есть его орбита становится квазигеостационарной. В течение 3,5 часов сигнал с него можно принимать на антенну диаметром 0,6 м без использования поворотного устройства. С другой стороны, точка квазигеостационара может быть расположена над любой точкой земного шара, а не только над экватором, как у геостационарных спутников. Это свойство используется в северных и южных широтах, сильно удалённых от экватора (выше 76 – 78° с.ш./ю.ш.), где угол места геостационарных спутников может быть очень низким, или даже отрицательным. В этих зонах приём с геостационарного спутника сильно затруднён или вовсе невозможен, и спутники на высокоэллиптических орбитах являются единственной возможностью обеспечить обслуживание. Углы мест у высокоэллиптических спутников превышают 40° на краях зоны обслуживания и достигают 90° в её центре. Орбиты ВЭО могут иметь любое наклонение, но часто имеют наклонение близкое к 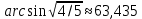 для обнуления возмущения вызванного неправильной формой Земли, похожей на сплюснутый эллипсоид. При использовании такого наклонения орбита стабилизируется. для обнуления возмущения вызванного неправильной формой Земли, похожей на сплюснутый эллипсоид. При использовании такого наклонения орбита стабилизируется.У эллиптических орбит аргумент перигея, находящийся между 180° и 360°, означает, что апогей находится над Северным полушарием. Если аргумент перигея находится между 0° и 180° – апогей находится над Южным полушарием. Апогей орбиты с аргументом перигея 0° или 180° будет находиться точно над экватором, что с практической точки зрения не имеет смысла, поскольку в этом случае дешевле и проще использовать КА на геостационарной орбите (понадобится всего лишь один спутник вместо трёх). Спутники на ВЭО обладают следующими достоинствами: возможность обслуживания очень большой территории. Так, например, такая система может обслуживать всю территорию России; возможность обслуживания высоких широт. Угол места в этих зонах у систем на ВЭО гораздо больше, чем у геостационарных спутников; широкое использование различных частотных диапазонов на ВЭО без регистрации (в отличие от геостационарной орбиты, где уже практически не осталось ни свободного места, ни свободных частот); более дешевый вывод на орбиту (примерно в 1,8 раза). В то же время, в настоящее время у систем на высокоэллиптических орбитах больше недостатков, чем достоинств. К недостаткам относятся: необходимость иметь, по крайней мере, три спутника на орбите (вместо одного геостационарного) для создания квазигеостационарной системы. В случае обеспечения круглосуточного непрерывного вещания, количество КА возрастает до семи; приемная антенна должна обладать функцией слежения (привод для разворота). Поэтому первоначальная стоимость такой антенны и стоимость её обслуживания будут выше, чем у простой фиксированной антенны; в высоких широтах плотность населения гораздо ниже, чем в средних районах, поэтому вопрос окупаемости такой системы очень сомнителен; апогей спутников на ВЭО выше, чем у ГСО, поэтому мощность передатчиков должна быть выше, до 400—500 ватт. Это удорожает спутники; орбита спутников на ВЭО обычно пересекает радиационные пояса, что сильно сокращает срок службы КА. Для того чтобы избавиться от этой проблемы, необходимо иметь орбиту с апогеем около 50 тыс. км и перигеем около 20 тыс. км; так как КА движутся по орбите, эффект Доплера создает дополнительные трудности для приемников на Земле; из-за большого времени распространения сигнала, возникают сложности при использовании приложений, работающих в реальном масштабе времени (например, телефония). Геопереходная орбита (ГПО) – орбита, являющаяся переходной между низкой опорной орбитой (НОО) (высота порядка 200 км) и геостационарной орбитой (ГСО) (35 786 км). В отличие от НОО и ГСО, которые в первом приближении являются круговыми, переходная орбита – это сильно вытянутая эллиптическая траектория движения КА, перигей которой лежит на расстоянии НОО от Земли, а апогей на расстоянии ГСО (орбита Гомана — Ветчинкина). Завершение вывода КА на ГСО происходит, когда он достигает апогея при движении по геопереходной орбите. В этот момент разгонный блок сообщает аппарату разгонный импульс, который превращает его эллиптическое движение в круговое, с периодом обращения вокруг Земли, равным длине суток. Геостационарная орбита (ГСО) – круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе координат направление на спутник не изменяется ни по азимуту ни по высоте над горизонтом, спутник «висит» в небе неподвижно. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т.п.). Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря. Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд (Звёздные сутки: 23 часа 56 минут 4,091 секунды). Преимущества геостационарной орбиты получили широкую известность после выхода в свет научно-популярной статьи Артура Кларка в журнале «Wireless World» в 1945 году, поэтому на Западе геостационарная и геосинхронные орбиты иногда называются «орбитами Кларка». А «поясом Кларка» называют область космического пространства на расстоянии 36000 км над уровнем моря в плоскости земного экватора, где параметры орбит близки к геостационарной. Первым спутником, успешно выведенным на ГСО, был Syncom-3, запущенный NASA в августе 1964 года. Спутник, находящийся на геостационарной орбите, неподвижен относительно поверхности Земли, поэтому его местоположение на орбите называется точкой стояния. В результате, сориентированная на спутник и неподвижно закреплённая направленная антенна может сохранять постоянную связь с этим спутником длительное время. Геостационарная орбита может быть точно обеспечена только на окружности, расположенной прямо над экватором, с высотой, очень близкой к 35 786 км. После завершения активной эксплуатации на остатках топлива спутник должен быть переведён на орбиту захоронения, расположенную на 200—300 км выше ГСО. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||