|
|
механика полёта. Механика полета. Механика
Недостатки геостационарной орбиты Задержка сигнала. Связь через геостационарные спутники характеризуется большими задержками в распространении сигнала. При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча «Земля-спутник» требует около 0,12 с. Ход луча «Земля (передатчик) → спутник → Земля (приемник)» ≈0,24 с. Ping (ответ) составит полсекунды (точнее 0,48 с). С учетом задержки сигнала в аппаратуре ИСЗ и аппаратуре наземных служб общая задержка сигнала на маршруте «Земля → спутник → Земля» может достигать 2—4 секунд. Такая задержка делает невозможной применение спутниковой связи с использованием ГСО в различных сервисах реального времени (например, в онлайн-играх). Невидимость ГСО с высоких широт. Геостационарная орбита не видна с высоких широт (приблизительно от 81° до полюсов). На широтах выше 75° ГСО наблюдается очень низко над горизонтом (в реальных условиях спутники просто скрываются выступающими объектами и рельефом местности) и виден лишь небольшой участок орбиты, то невозможна связь и телетрансляция с использованием ГСО в высокоширотных районах Крайнего Севера (Арктики) и Антарктиды. К примеру, американские полярники на станции Амундсен-Скотт для связи с внешним миром (телефония, интернет) используют оптоволоконный кабель длиной 1670 километров до расположенной на 75° ю.ш. французской станции Конкордия, с которой уже видно несколько американских геостационарных спутников. Солнечная интерференция. Одним из самых неприятных недостатков геостационарной орбиты является уменьшение и полное отсутствие сигнала в ситуации, когда солнце и спутник-передатчик находятся на одной линии с приёмной антенной (положение «солнце за спутником»). Данное явление присуще и другим орбитам, но именно на геостационарной, когда спутник «неподвижен» на небе, проявляется особенно ярко. В средних широтах северного полушария солнечная интерференция проявляется в периоды с 22 февраля по 11 марта и с 3 по 21 октября, с максимальной длительностью до десяти минут. В такие моменты в ясную погоду солнечные лучи, сфокусированные светлым покрытием антенны, могут повредить (расплавить или перегреть) приёмо-передающую аппаратуру спутниковой антенны. Международно-правовой статус ГСО
Использование геостационарной орбиты ставит целый ряд не только технических, но и международно-правовых проблем. Значительный вклад в их разрешение вносит ООН, а также её комитеты и иные специализированные учреждения.
Некоторые экваториальные страны в разное время предъявляли претензии (например, Декларация об установлении суверенитета на участке ГСО, подписанная в Боготе Колумбией, Конго, Эквадором, Индонезией, Кенией, Угандой и Заиром в 1976 г.) на распространение их суверенитета на находящуюся над их территориями часть космического пространства, в которой проходят орбиты геостационарных спутников. Было, в частности, заявлено, что геостационарная орбита является физическим фактором, связанным с существованием нашей планеты и полностью зависящим от гравитационного поля Земли, а потому соответствующие части космоса (сегменты геостационарной орбиты) как бы являются продолжением территорий, над которыми они находятся. Соответствующее положение закреплено в Конституции Колумбии.
Эти притязания экваториальных государств были отвергнуты, как противоречащие принципу неприсвоения космического пространства. В Комитете ООН по космосу такие заявления подверглись обоснованной критике. Во-первых, нельзя претендовать на присвоение какой-либо территории или пространства, находящегося на таком значительном удалении от территории соответствующего государства. Во-вторых, космическое пространство не подлежит национальному присвоению. В-третьих, технически неправомочно говорить о какой-либо физической взаимосвязи между государственной территорией и столь отдаленным районом космоса. Наконец, в каждом отдельном случае феномен геостационарного спутника связан с конкретным космическим объектом. Если нет спутника, то нет и геостационарной орбиты.
Скорости движения космических аппаратов на орбитах разного типа
Движению космических аппаратов по эллиптическим траекториям соответствуют так называемые эллиптические скорости, определяемые соотношением 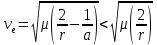 , частным случаем которых является круговая, или первая космическая скорость. , частным случаем которых является круговая, или первая космическая скорость.
Параболической траектории соответствует параболическая скорость 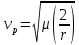 , называемая также второй космической скоростью. , называемая также второй космической скоростью.
Гиперболические скорости 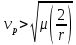 соответствуют движению по гиперболическим траекториям. соответствуют движению по гиперболическим траекториям.
Здесь μ – гравитационный параметр, равный 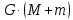 , где G —гравитационная постоянная, M – масса центрального тела, m – масса вращающегося тела; , где G —гравитационная постоянная, M – масса центрального тела, m – масса вращающегося тела; 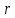 – расстояние между вращающимся телом и центральным телом; a – длина большой полуоси (для эллипса). – расстояние между вращающимся телом и центральным телом; a – длина большой полуоси (для эллипса).
Космическая скорость
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) – это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:
v1 (круговая скорость) – стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности);
v2 (параболическая скорость, скорость убегания) – преодолеть гравитационное притяжение небесного тела и уйти на бесконечность;
v3 – покинуть звёздную систему, преодолев притяжение звезды;
v4 – покинуть галактику.
Первая космическая скорость (круговая скорость) – минимальная скорость, которую необходимо придать объекту, чтобы вывести его на геоцентрическую орбиту. Иными словами, первая космическая скорость – это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
В инерциальной системе отсчёта на объект, движущийся по круговой орбите вокруг Земли, будет действовать только одна сила – сила тяготения Земли. При этом движение объекта не будет ни равномерным, ни равноускоренным. Происходит это потому, что скорость и ускорение (величины не скалярные, а векторные) в данном случае не удовлетворяют условиям равномерности/равноускоренности движения – то есть движения с постоянной (по величине и направлению) скоростью/ускорением. Действительно – вектор скорости будет постоянно направлен по касательной к поверхности Земли, а вектор ускорения – перпендикулярно ему к центру Земли, при этом по мере движения по орбите эти векторы постоянно будут менять свое направление. Поэтому в инерциальной системе отсчета такое движение часто называют «движение по круговой орбите с постоянной по модулю скоростью».
Часто для удобства вычисления первой космической скорости переходят к рассмотрению этого движения в неинерциальной системе отсчета – относительно Земли. В этом случае объект на орбите будет находиться в состоянии покоя, так как на него будут действовать уже две силы: центробежная сила и сила тяготения. Соответственно, для вычисления первой космической скорости необходимо рассмотреть равенство этих сил.
Точнее, на тело действует одна сила - сила тяготения, она же - центростремительная. Центробежная сила действует на Землю. Центростремительная сила, вычисляемая из условия вращательного движения равна силе тяготения. Отсюда, приравниванием этих формул, вычисляется скорость.
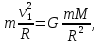
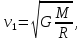
где m – масса объекта, M – масса планеты, G – гравитационная постоянная, v1 – первая космическая скорость, R – радиус планеты. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6371 км), найдем
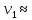 7,9 км/с. 7,9 км/с.
Первую космическую скорость можно определить через ускорение свободного падения. Поскольку
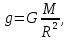
то 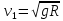 . .
Вторая космическая скорость (параболическая скорость, скорость освобождения, скорость убегания) – наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по дуге параболы относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой; если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.
Для получения формулы второй космической скорости удобно обратить задачу – спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
Запишем затем закон сохранения энергии
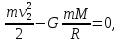
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния – энергия равна нулю). Здесь m – масса пробного тела, M – масса планеты, R – радиус планеты, G – гравитационная постоянная, v2 — вторая космическая скорость.
Решая это уравнение относительно v2, получим
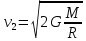 . .
Между первой и второй космическими скоростями существует простое соотношение:
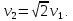
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности небесного тела):
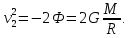
Вторая космическая скорость обычно определяется в предположении отсутствия каких-либо других небесных тел (например, для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики). Величины первой и второй космических скоростей для планет солнечной системы приведены в табл. 5.
Таблица 5
Первая (круговая) и вторая космическая скорость (скорость освобождения)
на поверхности некоторых небесных тел
Небесное тело
|
Масса (по отношению к массе Земли)
|
1-я космическая скорость, км/с
|
2-я космическая скорость, км/с
|
Луна
|
0,0123
|
1,680
|
2,4
|
Меркурий
|
0,055
|
3,05
|
4,3
|
Марс
|
0,108
|
3,546
|
5,0
|
Венера
|
0,82
|
7,356
|
10,22
|
Земля
|
1
|
7,91
|
11,2
|
Уран
|
14,5
|
15,6
|
22,0
|
Нептун
|
17,5
|
16,7
|
24,0
|
Сатурн
|
95,3
|
25
|
36,0
|
Юпитер
|
318,3
|
43
|
61,0
|
Солнце
|
333 000
|
437
|
617,7
|
Нейтронная звезда
|
666 000
|
|
200 000
|
Кварковая звезда
|
833 500
|
|
?
|
Чёрная дыра
|
832 500 - 5,6·1015
|
|
>299 792,458
|
Третья космическая скорость – минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.
Для расчёта третьей космической скорости можно воспользоваться следующей формулой:
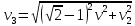 , ,
где v – орбитальная скорость планеты, v2 – вторая космическая скорость для планеты. Подставляя численные значения (для Земли v = 29,783 км/с, v2 = 11,182 км/с), найдем
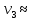 16,650 км/с. 16,650 км/с.
При старте с Земли, наилучшим образом используя осевое вращение (≈ 0,5 км/с) и орбитальное движение планеты (≈ 29,8 км/с), космический аппарат может достичь третьей космической скорости уже при
16,6 км/с относительно Земли. Для исключения влияния атмосферного сопротивления предполагается, что космический аппарат приобретает эту скорость за пределами атмосферы Земли. Наиболее энергетически выгодный старт для достижения третьей космической скорости должен осуществляться вблизи экватора, движение объекта должно быть сонаправлено осевому вращению Земли и орбитальному движению Земли вокруг Солнца. При этом скорость движения аппарата относительно Солнца составит
29,8 + 16,6 + 0,5 = 46,9 км/с.
Траектория аппарата, достигшего третьей космической скорости, будет частью ветви параболы, а скорость относительно Солнца будет асимптотически стремиться к нулю.
На 2012 год ещё ни один космический аппарат не покидал окрестностей Земли с третьей космической скоростью. Наибольшей скоростью покидания Земли обладал КА Новые горизонты – 16,21 км/с. За счёт гравитационного маневра у Юпитера, он покинет Солнечную систему со скоростью около 30 км/с после окончания основной части своей миссии. Аналогичным образом ускорялись и другие КА, уже покинувшие Солнечную систему (Вояджер-1, Вояджер-2, Пионер-10 и Пионер-11). Все они покидали окрестности Земли со скоростями, существенно меньшими третьей космической. |
|
|
 Скачать 1.01 Mb.
Скачать 1.01 Mb.
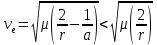 , частным случаем которых является круговая, или первая космическая скорость.
, частным случаем которых является круговая, или первая космическая скорость.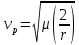 , называемая также второй космической скоростью.
, называемая также второй космической скоростью.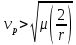 соответствуют движению по гиперболическим траекториям.
соответствуют движению по гиперболическим траекториям.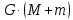 , где G —гравитационная постоянная, M – масса центрального тела, m – масса вращающегося тела;
, где G —гравитационная постоянная, M – масса центрального тела, m – масса вращающегося тела; 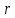 – расстояние между вращающимся телом и центральным телом; a – длина большой полуоси (для эллипса).
– расстояние между вращающимся телом и центральным телом; a – длина большой полуоси (для эллипса).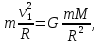
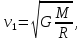
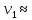 7,9 км/с.
7,9 км/с.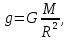
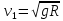 .
.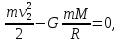
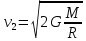 .
.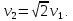
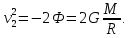
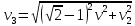 ,
,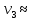 16,650 км/с.
16,650 км/с.