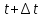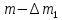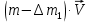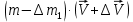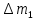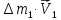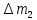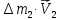механика полёта. Механика полета. Механика
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Уравнение движения точки переменной массы Реактивным движением называют движение тела, возникающее при отделении какой-либо его части. Э  Рис.5. Ракетный (а) и реактивный (воздушно-реактивный, б) двигатели: 1 – сопло, 2 – насос, 3 – камера сгорания, 4 – компрессор, 5 – форсунки. тот принцип преобразования энергии используют реактивные и ракетные двигатели (РД). Так почему они имеют несколько разное название? Что касается любого двигателя, то в любом из них происходит преобразование энергии топлива в энергию движения. Топливо включает в себя горючее и окислитель, необходимый для протекания химической реакции разложения горючего с выделением тепла (например, горение). Так вот, если двигатель, использующий реактивный принцип движения, получает окислитель из окружающего пространства (кислород воздуха земной атмосферы), такой двигатель принято называть реактивным двигателем (рис.5). Если же оба компонента топлива летательный аппарат несет на своем борту (то есть двигатель может работать на собственных компонентах при любых условиях в окружающем пространстве), то такой двигатель называют ракетным двигателем. Топливо ракетного двигателя может состоять из жидких (или сжиженных) компонентов. И в этом случае его называют жидкостным ракетным двигателем (ЖРД). РД, работающие на твердом топливе (баллистные пороха, смесевые ракетные топлива, включающие в себя горючее и окислитель) называют твердотопливными РД или ракетными двигателями твердого топлива (РДТТ). При полете ЛА с работающим реактивным двигателем происходит отбрасывание от него продуктов сгорания (ПС) топлива.А в случае, если на ЛА установлен воздушно-реактивный двигатель, то кроме отбрасывания ПС топлива на ЛА поступают все новые и новые частицы воздуха, т.е. состав (масса) ЛА в процессе полета при любом типе двигателя непрерывно меняется. Рассматривая движение ЛА удобно в каждый момент времени включать в его состав только те частицы, которые в данный момент времени находятся внутри объема ЛА. При такой постановке ЛА с работающим двигателем представляет собой систему переменного состава, к которой непосредственно нельзя применить теоремы динамики твердого тела. Однако основываясь на этих классических теоремах И.В.Мещерский доказал аналогичные теоремы для системы материальных точек переменной массы и установил принцип составления уравнений движения реактивного ЛА. Теорема об изменении количества движения системы материальных точек Будем считать, что масса интересующего нас объекта в какой-то промежуток времени 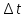 будет изменяться за счет отсоединения и присоединения масс частиц. Допустим, что в момент времени t частица массой m движется со скоростью V. будет изменяться за счет отсоединения и присоединения масс частиц. Допустим, что в момент времени t частица массой m движется со скоростью V.Используем теорему об изменении количества движения системы материальных точек на промежутке времени 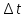 . .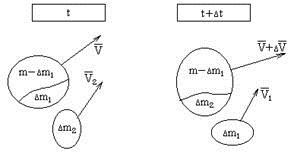 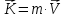 – количество движения; – количество движения;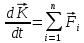 – сумма внешних сил. – сумма внешних сил.
Определим приращение количества движения системы материальных точек за промежуток времени 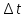 : :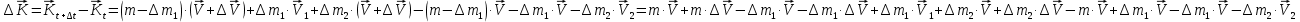 . .То есть 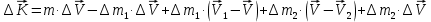 . . Рассматривая изменение количества движения за малый промежуток времени и учитывая только члены первого порядка малости, получаем: 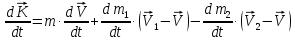 . .Здесь 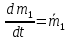 – расход топлива; – расход топлива;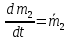 – приход топлива; – приход топлива; 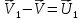 – относительная скорость отсоединения частиц; – относительная скорость отсоединения частиц;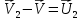 – относительная скорость присоединения частиц. – относительная скорость присоединения частиц.Таким образом, получаем уравнение: 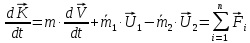 . .Уравнение Мещерского для поступательного движения тела переменной массы:
Формула Циолковского Запишем уравнение Мещерского: 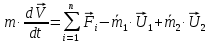 . Будем рассматривать движение ракеты в безвоздушном пространстве и вне поля тяготения Земли, т.е. ракета движется под действием силы тяги. Для нашего случая уравнение Мещерского будет иметь вид: . Будем рассматривать движение ракеты в безвоздушном пространстве и вне поля тяготения Земли, т.е. ракета движется под действием силы тяги. Для нашего случая уравнение Мещерского будет иметь вид: 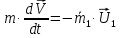 ; ;Здесь 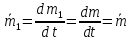 , ,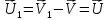 – относительная скорость отсоединяемых частиц. Для ракеты это скорость истечения газов из сопла двигателя (скорость на срезе сопла). – относительная скорость отсоединяемых частиц. Для ракеты это скорость истечения газов из сопла двигателя (скорость на срезе сопла).Таким образом: 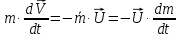 . Как правило, для ракеты . Как правило, для ракеты 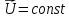 , и, следовательно, , и, следовательно, 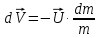 – дифференциальное уравнение с раздельными переменными. – дифференциальное уравнение с раздельными переменными.Проинтегрируем это равнение: 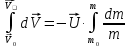 . . В результате имеем 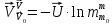 . Отсюда . Отсюда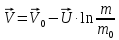 – формула скорости Циолковского. – формула скорости Циолковского.Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической и при 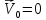 может быть записана, как: может быть записана, как: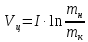 , ,где: 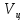 – конечная (после выработки всего топлива) скорость летательного аппарата – скорость Циолковского; – конечная (после выработки всего топлива) скорость летательного аппарата – скорость Циолковского;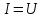 – удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива), равный скорости истечения продуктов сгорания из сопла ракетного двигателя; – удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива), равный скорости истечения продуктов сгорания из сопла ракетного двигателя;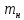 – начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо); – начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо);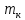 – конечная масса летательного аппарата (полезная нагрузка + конструкция). – конечная масса летательного аппарата (полезная нагрузка + конструкция).Для многоступенчатой ракеты конечная скорость рассчитывается как сумма скоростей, полученных по формуле Циолковского отдельно для каждой ступени, причем при расчёте характеристической скорости каждой ступени к её начальной и конечной массе добавляется суммарная начальная масса всех последующих ступеней. Введем обозначения:  – масса заправленной i-ой ступени ракеты; – масса заправленной i-ой ступени ракеты;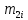 – масса i-ой ступени без топлива; – масса i-ой ступени без топлива;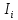 – удельный импульс двигателя i-ой ступени; – удельный импульс двигателя i-ой ступени;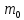 – масса полезной нагрузки; – масса полезной нагрузки;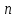 – число ступеней ракеты. – число ступеней ракеты.Тогда формула Циолковского для многоступенчатой ракеты может быть записана в следующем виде: 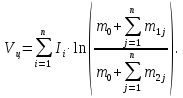 Системы координат 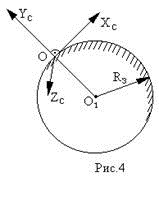 Рассмотрим три системы координат: Стартовая система координат. Э Рис.6 та система связана с Землей (рис. 6) и вращается вместе с ней. Начало координат расположено в точке старта. Ось OYc направлена в сторону противоположную силе тяжести. Ось OXc перпендикулярна оси OYc и направлена в сторону цели. Ось OZc соответствует правой системе координат. Плоскость XcOYc называется плоскостью стрельбы. Связанная система координат. П 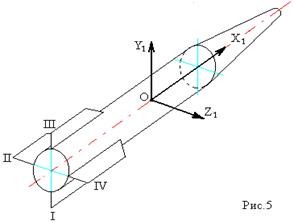 редставляет собой декартовую прямоугольную правую систему осей координат, неподвижную относительно ракеты (рис. 7) или ГЧ (рис. 8). Оси этой системы называют связанными осями. редставляет собой декартовую прямоугольную правую систему осей координат, неподвижную относительно ракеты (рис. 7) или ГЧ (рис. 8). Оси этой системы называют связанными осями.Н Рис.7 ачало связанной системы координат помещено в центр тяжести (или в центр масс) ракеты. Ось OX1 направлена по продольной оси ракеты в сторону ГЧ. Ось OY1 расположена в плоскости симметрии ракеты, которая в момент старта совпадает с плоскостью стрельбы (плоскостью XcOYc) стартовой системы координат. Ось OY1 направлена в сторону третьего, а ось OZ1 – в сторону четвертого стабилизатора. Для ГЧ направление осей OY1 и OZ1 удобно выбрать так, чтобы для ГЧ, состыкованной с ракетой, ось OY1 была направлена в сторону третьего стабилизатора, а ось OZ1 – в сторону четвертого. П 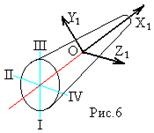 Рис.8 ри установке ракеты на стартовый стол плоскость стабилизаторов I и III совпадает с плоскостью стрельбы, а стабилизатор I направлен в сторону цели. Связанная система координат иногда называется “подвижной” системой координат. С 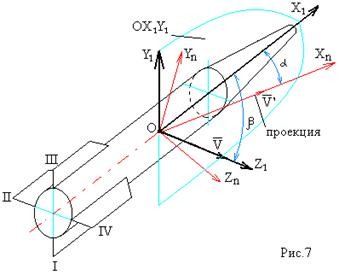 коростная система координат. Это также декартовая, прямоугольная, правая система координат (рис. 9). Начало системы (точка О) расположено в центре тяжести ракеты. Ось OХn направлена по вектору скорости ракеты коростная система координат. Это также декартовая, прямоугольная, правая система координат (рис. 9). Начало системы (точка О) расположено в центре тяжести ракеты. Ось OХn направлена по вектору скорости ракеты 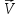 . Ось OYn перпендикулярна OXn и лежит в плоскости симметрии ракеты OX1Y1. . Ось OYn перпендикулярна OXn и лежит в плоскости симметрии ракеты OX1Y1.Ориентация ракеты относительно вектора скорости 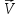 в общем случае определяется двумя углами: в общем случае определяется двумя углами:у Рис.9 гол атаки 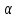 – это угол между проекцией вектора скорости – это угол между проекцией вектора скорости 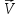 на плоскость симметрии ракеты OX1Y1 и продольной осью ракеты OX1. на плоскость симметрии ракеты OX1Y1 и продольной осью ракеты OX1.угол скольжения 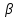 – это угол между вектором скорости – это угол между вектором скорости 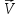 и плоскостью ракеты OX1Y1. и плоскостью ракеты OX1Y1.Силы и моменты, действующие на ракету в полете. Аэродинамические силы Силовое воздействие сплошной газообразной среды сводится к непрерывно распределенным по поверхности тела силам от нормальных напряжений и от касательных напряжений. Все аэродинамические силы, действующие на ракету в полете можно свести к одной результирующей силе RA (главная аэродинамическая сила), а также к результирующему моменту МА, действующему относительно центра масс ракеты. RA проходит через точку на продольной оси ракеты, которая носит название центр давления. Величина и направление RA и МА зависят от ряда факторов, в том числе: от угла атаки, плотности воздуха, скорости воздушного потока, аэродинамической формы ракеты и т.д. Известно, что RA в наибольшей степени, кроме формы ракеты, зависит от угла атаки 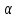 и от угла скольжения и от угла скольжения 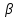 . .Для того, чтобы было удобно составлять уравнения движения, принято RA и МА раскладывать по осям систем координат (рис. 10). – По осям скоростной системы координат RA есть: 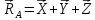 . .Проекция RA на ось OXn ( 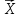 ) всегда отрицательна и носит название силы лобового сопротивления; ) всегда отрицательна и носит название силы лобового сопротивления;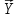 – подъемная сила; – подъемная сила;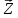 – боковая сила. – боковая сила.– По осям связанной системы координат RA есть:  . .З 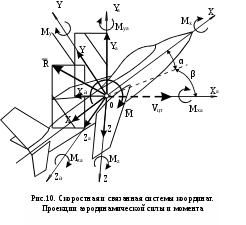 десь Х1 – продольная (осевая) сила; Y1 – нормальная сила; Z1 – поперечная сила. Баллистическая ракета является аэродинамически осесимметричным телом. Если продольная ось ракеты направлена по вектору скорости (т.е. 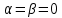 ), то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящую через эту ось, т.е. Y1 = Y = 0; Z1 = Z = 0. ), то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящую через эту ось, т.е. Y1 = Y = 0; Z1 = Z = 0.Если ось ракеты образует с вектором скорости некоторый угол, то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящей через ось ракеты и вектор скорости. При этом RA и ее составляющие (X,X1,Y,Y1) будут лежать в этой плоскости, следовательно, для аэродинамики симметричной ракеты зависимости силы Z(Z1) от угла скольжения 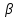 аналогичны зависимостям силы Y(Y1) от угла атаки аналогичны зависимостям силы Y(Y1) от угла атаки 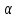 . . На основании теории аэродинамического подобия проекции аэродинамической силы на оси системы координат (связанной или скоростной) равны: 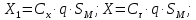 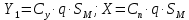 , , 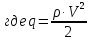 – скоростной напор, действующий на ракету; – скоростной напор, действующий на ракету;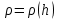 – плотность воздуха на высоте полета; – плотность воздуха на высоте полета;V – скорость ракеты; Sм – характерная площадь ЛА (для бескрылого ЛА или фюзеляжа это площадь наибольшего – миделевого сечения), которая для ракеты равна; 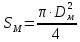 , где Dм – диаметр цилиндрической части ракеты; , где Dм – диаметр цилиндрической части ракеты;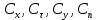 – безразмерные аэродинамические коэффициенты. – безразмерные аэродинамические коэффициенты.Аэродинамические коэффициенты зависят от формы ракеты, ее ориентации относительно вектора воздушной скорости (т.е. от величины углов 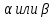 ), а также от критериев аэродинамического подобия. ), а также от критериев аэродинамического подобия.Критериями аэродинамического подобия являются: – число Маха 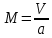 ; ;– число Рейнольдса 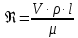 ; ; здесь а = а(h) – скорость звука в воздушной среде на данной высоте; l – характерный размер ЛА (для ракеты – длина ракеты); 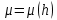 – динамический коэффициент вязкости воздуха. – динамический коэффициент вязкости воздуха. | |||||||||||||||