механика полёта. Механика полета. Механика
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Используемые двигатели. В качестве маршевых двигателей могут использоваться: жидкостные ракетные двигатели; твёрдотопливные ракетные двигатели; различные комбинации на разных ступенях. Масса полезной нагрузки. В зависимости от массы полезного груза ракеты-носители делятся на следующие классы: ракеты сверхтяжёлого класса (больше 50 тонн); ракеты тяжелого класса (до 30 тонн); ракеты среднего класса (до 15 тонн); ракеты лёгкого класса (до 2-4 тонн); ракеты сверхлёгкого класса (до 300-400 кг). Конкретные границы классов меняются с развитием техники и являются достаточно условными, в настоящее время лёгким классом считаются ракеты, выводящие на низкую опорную орбиту груз массой до 5 т, средними — от 5 до 20 т, тяжёлыми — от 20 до 100 тонн, сверхтяжёлыми — свыше 100 т. Появляется также новый класс так называемых «нано-носителей» (полезная нагрузка – до нескольких десятков кг). Повторное использование. Наибольшее распространение получили одноразовые многоступенчатые ракеты, как пакетной, так и продольной компоновки. Одноразовые ракеты отличаются высокой надёжностью благодаря максимальному упрощению всех элементов. Следует уточнить, что одноступенчатой ракете для достижения орбитальной скорости теоретически необходимо иметь конечную массу не более 7—10 % от стартовой, что при даже существующих технологиях делает их труднореализуемыми и экономически неэффективными из-за низкой массы полезного груза. В истории мировой космонавтики одноступенчатые ракеты-носители практически не создавались –существовали только т. н. полутораступенчатые модификации (например, американской РН «Атлас» со сбрасываемыми дополнительными стартовыми двигателями). Наличие нескольких ступеней позволяет существенно увеличить отношение массы выводимой полезной нагрузки к начальной массе ракеты. В то же время многоступенчатые ракеты требуют отчуждения территорий для падения промежуточных ступеней. Ввиду необходимости применения высокоэффективных сложных технологий (прежде всего, в области двигательных установок и теплозащиты), полностью многоразовых ракет-носителей пока не существует, несмотря на постоянный интерес к этой технологии и периодически открывающиеся проекты разработки многоразовых носителей (за период 1990—2000-х годов – такие, как: ROTON, Kistler K-1, АКС VentureStar и др.). Частично многоразовой являлась широко использовавшаяся американская многоразовая транспортная космическая система (МТКС)-АКС «Спейс шаттл» («Космический челнок») и закрытая советская программа МТКС «Энергия –Буран», разработанная, но так и не использованная в прикладной практике, а также ряд нереализованных бывших (например, «Спираль», МАКС и др. АКС) и вновь разрабатываемых (например, «Байкал-Ангара») проектов. Вопреки ожиданиям, «Спейс шаттл» не смог обеспечить снижение стоимости доставки грузов на орбиту; кроме того, пилотируемые МТКС характеризуются сложным и длительным этапом предстартовой подготовки (из-за повышенных требований по надёжности и безопасности при наличии экипажа). Присутствие человека. Ракеты для пилотируемых полётов должны обладать большей надёжностью (также на них устанавливается система аварийного спасения); допустимые перегрузки для них ограничены (обычно не более 3—4,5 единиц). При этом сама ракета-носитель является полностью автоматической системой, выводящей в космическое пространство аппарат с людьми на борту (это могут быть как пилоты, способные осуществлять непосредственное управление аппаратом, так и так называемые «космические туристы»). Основные задачи, решаемые для баллистической ракеты Баллистическая ракета – ракета, полет которой в основном совершается по траектории свободно брошенного тела. Баллистическая ракета в отличие от крылатой ракеты не имеют несущих поверхностей, предназначенных для создания подъемной силы при полете в атмосфере. Могут быть управляемыми и неуправляемыми, одно- и многоступенчатыми. Боевые баллистические ракеты по назначению подразделяются на стратегические, оперативно-тактические и тактические. Морские баллистические ракеты устанавливаются на подводных лодках. Пуск может проводиться из подводного и надводного положений. Ракета-носитель (РН) – многоступенчатая (2—4 ступени) баллистическая ракета для выведения в космос искусственных спутников Земли, автоматических межпланетных станций, космических кораблей, орбитальных станций и др. полезных грузов. В зависимости от энергетических характеристик и способности выводить на орбиту искусственного спутника полезный груз определённой массы РН можно условно разделить на следующие классы: лёгкие (до 500 кг), средние (до 10 т), тяжёлые (до 100 т), сверхтяжёлые (свыше 100 т). Большинство РН создано на основе межконтинентальных баллистических ракет или баллистических ракет средней дальности. Задачи, ставящиеся при проектировании ракет: 1. Исследование летных характеристик ЛА и в первую очередь дальности, в зависимости от конструктивных параметров ЛА с целью выбора наивыгоднейшего сочетания этих параметров. 2. Определение траектории и других характеристик ЛА с известными конструктивными параметрами, с известной системой управления при заданных прицельных дальностях полета для управляемых баллистических ракет. 3. Определение исходных данных для проектирования головных частей и исследование рассеивания головных частей. 4. Обеспечение максимальной прицельной дальности стрельбы в условиях влияния различных возмущающих факторов: разброса конструктивных параметров, изменение внешних условий полета и т.д. 5. Исследование влияния различных возмущающих факторов на активном участке полета ракеты. 6. Определение прицельных данных по заданным координатам точки старта и точки целей. 7. Выбор такой траектории полета, которая обеспечит наилучшее использование возможностей ЛА. 8. Определение исходных данных для летно-конструкторских испытаний и анализ этих испытаний. При решении этих задач возникает ряд и других вопросов: – аэродинамика – определение величин аэродинамических сил, моментов, нагрева поверхности и элементов конструкции ракеты и головной части (ГЧ); – динамика конструкций – расчет упругих колебаний и колебаний жидкостей в баках; – управление полетом ЛА – это обеспечение устойчивости движения, обеспечение управляемости полетом ракеты с учетом упругих колебаний и колебаний жидкости в баках; выбор структуры и основных параметров системы управления; – динамика неустановившихся режимов полета, имеющих место при старте ракеты, разделении ступеней, отделении ГЧ (обеспечение безопасности разделения и управляемости ракеты на этих участках полета); – расчет конструкции ЛА на прочность – определение нагрузок, действующих на конструкцию ЛА на различных участках траектории полета. Движение, форма и гравитационное поле Земли Движение Земли Земля при своем движении в космическом пространстве совершает сложное движение, которое состоит из следующих составляющих: 1. Вращение вокруг своей оси с запада на восток с периодом 23 часа 56 минут 4.091 секунды среднего солнечного времени (86164,091 с) или 24 ч = 86400 с звездного времени; угловая скорость вращения Земли при этом равна 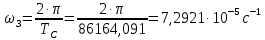 ; вектор угловой скорости Земли направлен по оси вращения от южного полюса к северному (в соответствии с правой системой координат). ; вектор угловой скорости Земли направлен по оси вращения от южного полюса к северному (в соответствии с правой системой координат).2. Годичное вращение Земли вокруг Солнца со средней скоростью Vз = 298,93 км/с. 3. Нутационные колебания земной оси с периодом 18,6 года и с амплитудой, не превышающей 9.2” (угловых секунд). В процессе нутационных колебаний ось описывает конусообразную поверхность вокруг некоторого среднего положения, которое совпадает с вектором кинетического момента Земли. 4. Прецессионное3 движение Земли относительно оси эклиптики4 с периодом 25800 лет. 5. Движение Земли вместе с солнечной системой относительно других звезд. Вращение Земли вокруг своей оси относительно неподвижных звезд определяет звездное время. Вращение Земли вокруг своей оси относительно центра Солнца определяет истинное солнечное время. При исследовании движения баллистических ракет все составляющие движения Земли, кроме его суточного вращения не учитываются, т.к. их влияние на траекторию полета ракеты ничтожно мало. При расчете траектории полета зенитной управляемой ракеты (ЗУР) Земля считается неподвижной. Считается, что центр Земли движется прямолинейно и равномерно и Земля вращается равномерно вокруг своей оси, положение в пространстве не меняется. Вращение Земли оказывает существенное влияние на динамику полета баллистических ракет (БР), т.к. при движении ракеты необходимо учитывать силы инерции, вызванные суточным вращением Земли. Форма Земли Земля представляет собой геометрическое тело сложной формы. Поверхность Земли со всеми ее неровностями называется физической поверхностью Земли. Из геометрических тел, описывающих форму Земли, наиболее близко к реальной Земле подходит геоид. Г 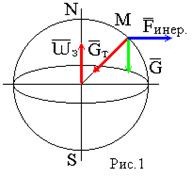 еоид – представляет собой тело ограниченное уровенной поверхностью силы тяжести, совпадающей с поверхностью океана (невозмущенной приливами и волнами) и продолженной под материками. Поверхность геоида непрерывно замкнута и не имеет резких перегибов и складок. еоид – представляет собой тело ограниченное уровенной поверхностью силы тяжести, совпадающей с поверхностью океана (невозмущенной приливами и волнами) и продолженной под материками. Поверхность геоида непрерывно замкнута и не имеет резких перегибов и складок.Fинер – сила инерции Gт – сила притяжения G – сила тяжести Примечание: экспериментальным путем невозможно отделить центробежную силу инерции от силы земного притяжения. Известно, что массы пород внутри Земли распределены неравномерно и направление силы тяжести в различных точках Земли зависит от этого распределения, поэтому поверхность геоида является весьма сложной и не имеет математического описания. В первом приближении Землю можно считать шаром, объем которого равен объему Земли, а радиус  . .В большинстве случаев с достаточной для практического использования точностью геоид можно заменить эллипсоидом вращения, полученным вращением эллипса вокруг малой оси. Эллипсоид, который наилучшим образом приближается к поверхности реального геоида, носит название общего земного эллипсоида. Он определяется из следующих условий: – центр эллипсоида совпадает с центром Земли, а плоскость его экватора совпадает с плоскостью экватора Земли. – объемы эллипсоида и геоида равны. – сумма квадратов отклонений (по высоте) к поверхности общего земного эллипсоида от поверхности геоида должна быть минимальной. В настоящее время приняты следующие размеры общего земного эллипсоида: – большая полуось (радиус экватора) а = 6378137 м, – малая полуось b = 6356752 м, сжатие эллипсоида – 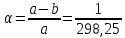 . .По мнению ряда ученых, поверхность даже самого точного эллипсоида, правильно ориентированного по отношению к Земле, может отклоняться от поверхности геоида на величины ± 150 м. В некоторых странах, больших по площади, с целью уменьшения геодезических ошибок, появляющихся от замены геоида общим земным эллипсоидом, вводят понятие о референс эллипсоиде. Им называют эллипсоид вращения с соответствующими размерами, определенным образом ориентированным относительно поверхности Земли и к поверхности которого относятся результаты геодезических работ на рассматриваемом участке земной поверхности в данном государстве. Так на территории России за размеры референс эллипсоида приняты размеры Красовского: а = 6378245 м; b = 6357520 м; 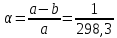 . .Гравитационное поле Земли Согласно второму закону Ньютона (закон тяготения) каждая частица массой М притягивает другую частицу массой m силой гравитационного притяжения (тяготения) Gт, определяемой следующей зависимостью: 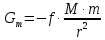 , ,где f – гравитационная постоянная; r – расстояние между частицами. Если эту формулу применить к Земле, то для приближенных расчетов: 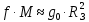 , где , где 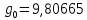 м/с2 – ускорение земного притяжения для м/с2 – ускорение земного притяжения для  . .Тогда 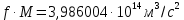 . .При полете ЛА, на них действуют силы притяжения Земли и других небесных тел. При полете ЛА на небольшом расстоянии от Земли действие небесных тел (Луна, Солнце и т.д.) незначительно или ими пренебрегают. Сила притяжения Земли консервативна, т.е. имеет силовую функцию. G – зависит от географического положения точки (ее долготы и широты). Для удобства расчетов принимаем, что сила притяжения Земли G = const. Атмосфера При полете ЛА на небольшом расстоянии от Земли, на него кроме силы тяжести действуют аэродинамические силы. Величина этих сил зависит от конструкции ЛА, а также от состояния параметров атмосферы (температура, плотность, давление). Параметры атмосферы в свою очередь зависят: – от географической широты места полета; – от времени суток; – от времени года; – от активности Солнца и т.д. При расчете траектории ЛА при его проектировании используются значения стандартной атмосферы (СА), которые представляют собой некоторые средние значения параметров спокойной атмосферы в зависимости от высоты полета. ГОСТ 4401-81 определяет параметры СА до высоты 200 км. За начало отсчета высоты принят уровень моря ( 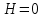 ), для которого стандартное атмосферное давление равно 760 мм рт. ст. = 101 325 Па; стандартная температура 288,15 К; стандартная плотность 1,225 кг/м3, стандартная концентрация ), для которого стандартное атмосферное давление равно 760 мм рт. ст. = 101 325 Па; стандартная температура 288,15 К; стандартная плотность 1,225 кг/м3, стандартная концентрация 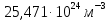 на географической широте 45о32′33′′ при молярной массе М = 28,964 42 кг/кмоль. на географической широте 45о32′33′′ при молярной массе М = 28,964 42 кг/кмоль.По изменению температуры в атмосфере выделяют характерные области, носящие названия «сферы» и «паузы» (рис.2). Сфера – слой атмосферы, в пределах которого происходит изменение температуры, а пауза – слой атмосферы с постоянной температурой. В основе закономерностей, принятых в СА, лежит опытный закон изменения температуры с высотой. Условились считать, что в пределах сфер зависимость температуры от высоты линейная, а для пауз характерно постоянство температуры. Так для тропосферы температурный градиент составляет примерно 0,006 5 град/м, т. е. закон изменения температуры с высотой можно записать как 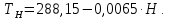 В области тропопаузы (на высотах более 11 км) температура воздушной среды равна 216,65 К. Температурный градиент для стратосферы составляет примерно +0,002 8 град/м, а в мезосфере температура снижается с интенсивностью около 0,003 5 град/м (см. рис. 2). Д  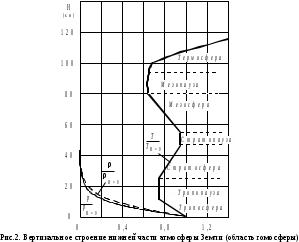 ля высот до 80 км включительно для каждого слоя атмосферы получены полуэмпирические зависимости T, p и ρ от H, позволяющие достаточно просто рассчитать параметры СА. Зависимости давления и плотности от высоты имеют сложный вид. Для практических расчетов используют модель экспоненциального закона изменения этих параметров с ростом высоты, причем показатели экспоненты учитывают изменение температуры атмосферы. Следует заметить, что уменьшение давления происходит более интенсивно, чем уменьшение плотности. ля высот до 80 км включительно для каждого слоя атмосферы получены полуэмпирические зависимости T, p и ρ от H, позволяющие достаточно просто рассчитать параметры СА. Зависимости давления и плотности от высоты имеют сложный вид. Для практических расчетов используют модель экспоненциального закона изменения этих параметров с ростом высоты, причем показатели экспоненты учитывают изменение температуры атмосферы. Следует заметить, что уменьшение давления происходит более интенсивно, чем уменьшение плотности.Зависимость СА от высоты подобрана таким образом, что СА ближе всего подходит к средним широтам северного полушария в летнее время. Основные компоненты, составляющие атмосферу Земли, – это азот (78 %) и кислород (21 %). Отклонение параметров атмосферы от стандартных значений, а также перемещение воздушных масс (ветер) представляют собой атмосферные возмущения, которые влияют на параметры полета, ЛА. При проектировании ЛА необходимо знать диапазоны возможных отклонений этих параметров, знать статистические зависимости между случайными отклонениями каждого параметра на разных высотах от времени года, географической широты и т.д. Системы координат Определение положения точки на земной поверхности Для определения положения точки на земной поверхности математического описания гравитационного поля Земли используют в основном две системы координат: 1 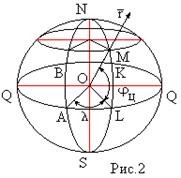 . Геоцентрическая система координат (рис. 3). . Геоцентрическая система координат (рис. 3).Положение точки М на поверхности эллипсоида Красовского определяют две координаты: λ Рис. 3 Геоцентрическая система координат (долгота) – угол между плоскостью Гринвичского меридиана и плоскостью местного меридиана, проходящего через точку М. Долготы точек, расположенные восточнее Гринвичского меридиана, принято считать положительными, а западнее – отрицательными. φц (геоцентрическая широта) – угол между экватором и радиусом, проведенным из центра эллипсоида через точку М. Широты, лежащие выше экватора (северные) – положительные, а южные – отрицательные. 2 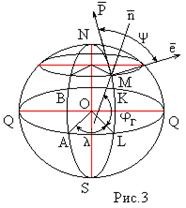 . Геодезическая система координат (рис. 4). . Геодезическая система координат (рис. 4).В этой системе положение точки на поверхности эллипсоида Красовского также определяются по двум координатам: λ (долгота) – определяется как в геоцентрической системе координат. φ Рис. 4 Геодезическая система координат г (геодезическая широта) – угол между плоскостью экватора и нормалью к поверхности эллипсоида в точке М. Геодезическим азимутом направления L называется угол ψ, отсчитываемый по часовой стрелке от северного направления  геодезического меридиана данной точки, до заданного направления. геодезического меридиана данной точки, до заданного направления.Широты φw и φг связаны между собой следующим соотношением: 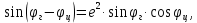 где е – эксцентриситет меридионального эллипса и общего земного эллипсоида. |
