УПП_Дискретная математика-1. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики

• Название: Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
• Дата: 09.02.2023
• Размер: 6.65 Mb.
• Имя файла: УПП_Дискретная математика-1.doc
• Тип: Учебно-практическое пособие; #929287
• страница: 3 из 19

1.2. Отношения на множествах

Предложения «х – брат y», «x
Первое предложение свидетельствует, что два объекта «х» и «y» принадлежат общему классу – сыновья общих родителей. Второе предложение выражает относительный порядок в системе.

Об отношении можно говорить тогда, когда можно выделить множество объектов, на которых это отношение определено.

Приведенные примеры есть бинарные отношения (они выполняются для пары объектов). Тернарные отношения определены для трех объектов, n-арные – для n объектов.

Отношением А на множестве М называют подмножество А множества ММ. Если входит в А, то обозначают xAy (A). Эта запись читается так: «х находится в отношении А с y».

Итак, отношением называется упорядоченная пара <А,М>, где АММ, М – множество, на котором определено отношение, А – множество пар, для которых это отношение определено. (Рассматриваем бинарные отношения).

Обратимся к примеру. Зададим отношение «x_i – победитель x_j» в шахматном турнире из пяти игроков х₁, х₂, х₃, х₄, х₅, турнир игрался в один круг. Данные приведены в табл. 1.2.1.
Таблица 1.2.1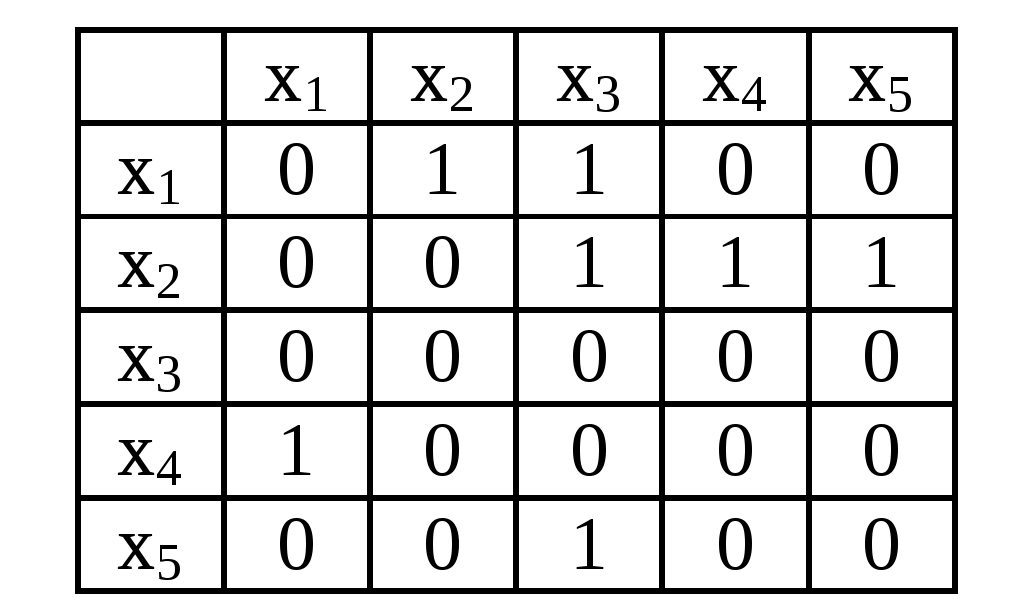


i^ая строка соответствует элементу х_i, j^ый столбец элементу х_j, на их пересечении ставится 1, если отношение х_iАх_j выполнено, и 0, если нет. Так, единица, стоящая на пересечении 4^ой строки и 1^го столбца, соответствует тому, что игрок х₄ выиграл у игрока х₁, т.е. <х₄Ах₁>.

Итак, на множестве М(х₁, ... х₅) отношение «x_i – победитель y_j» задано матрицей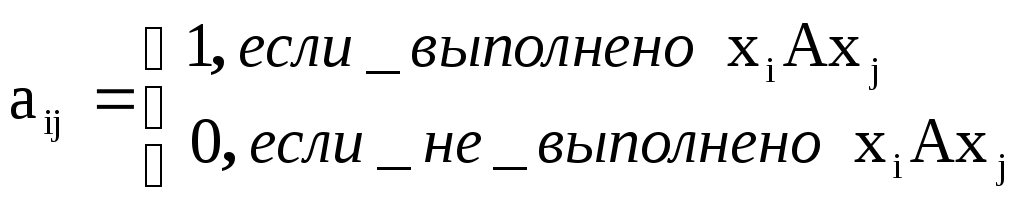

Такая матрица полностью задает отношение А на множестве М. Прямое произведение ММ представлено двадцатью пятью элементами матрицы (табл. 1.2.1).

Если a_ij0 , то имеем пустое отношение, т.е. такое, которое не выполнено ни для какой пары х_iх_j. Если a_ij1, имеем полное отношение, т.е. отношение, выполненное для всех пар. Единичная матрица Е задает диагональное отношение, отношение равенства: <х_iАх_j>, если хi=хj.

Зададим отношение другим способом, а именно: элементы множества изобразим точками, проведем стрелку от х_i к х_j, если выполнено х_iАх_j, получим фигуру – ориентированный граф (рис. 1.2.1).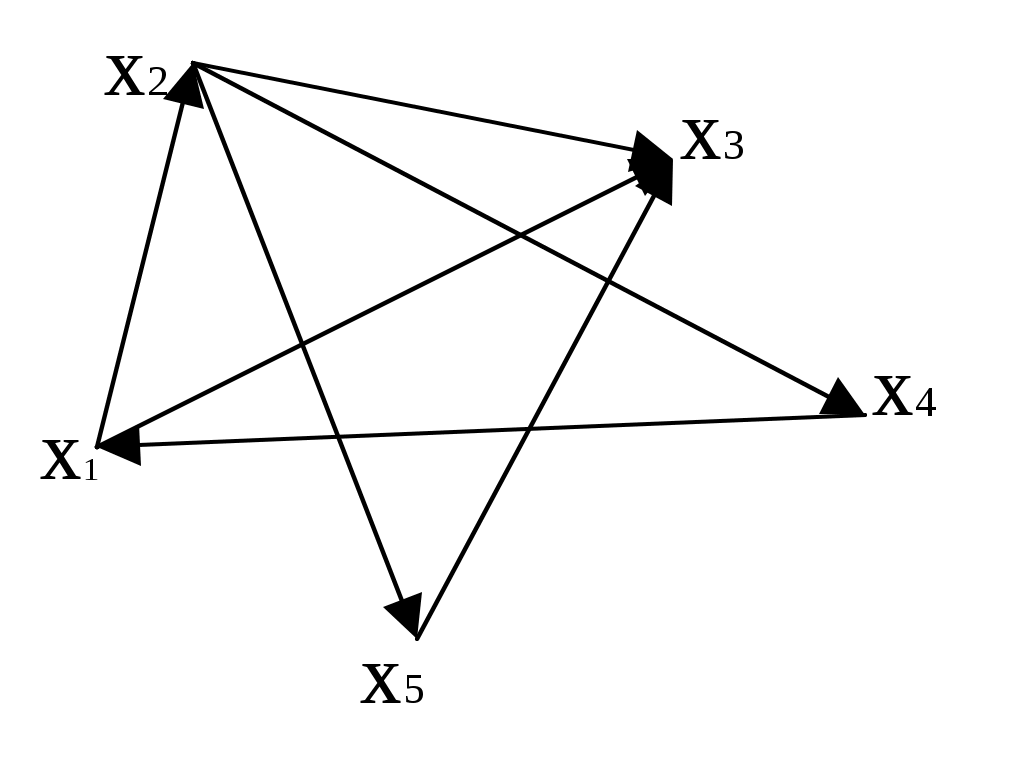


Рис. 1.2.1
Точки х₁, х₂, х₃, х₄, х₅ – вершины графа, направленные линии – ребра графа.

Элементы теории графов рассмотрим во второй части данного пособия.
Свойства отношений:

1. 
   Отношение А рефлексивно, если оно выполнено между объектом и им самим, т.е. хАх.
   

Отношения «быть похожим», «быть знакомым» – рефлексивны. Отношение «быть братом» – нерефлексивно.

2. 
   Если отношение А может выполняться лишь для несовпадающих объектов, то оно антирефлексивно, т.е. из хАу следует, что ху.
   
3. 
   Отношение А называется симметричным, если при выполнении хАу выполнено уАх.
   

Отношения «быть родственником», «быть похожим на» – симметричны.

4. 
   Отношение А называется асимметричным, если из двух отношений хАу и уАх хотя бы одно не выполнено. Так, приведенный выше пример: отношение «x – победитель y» – асимметрично.
   

Справедлива теорема: если отношение асимметрично, то оно антирефлексивно.

5. 
   Отношение называется транзитивным, если при выполнении хАу и уАz выполнено хАz.
   

Примером является отношение «быть больше (меньше)». Так, если х<у и у

6. 
   Отношение А называется антисимметричным, если оба соотношения хАу и уАх выполняются только тогда, когда х=у.
   

Эквивалентность. Отношение эквивалентности определяется отображением множества Х на множество Y и характеризуется разбиением множества Х на классы.
Множество Х разбито на классы, если его можно представить в виде суммы непересекающихся подмножеств:
X=X₁X₂ ... X_n,

где X_kX и X_iX_j=V (ij) .
Так, множество Х учащихся десятых классов некоторой школы разбивается на два класса: Х₁ – учащиеся класса, Х₂ – учащиеся класса. X=X₁X₂ и X₁X₂=V, т.к. нет учеников, обучающихся одновременно и в , и в классе.

Два элемента множества Х эквивалентны, если они принадлежат одному и тому же классу.

Каждая пара учащихся класса – эквивалентные элементы множества Х₁ (так же, как и пара – Х₂).

Разбивая множество Х на классы, мы осуществили сюръективное отображение множества всех учащихся Х на множество Y, состоящее из двух элементов у₁= ,у₂= . Причем , .
Другой пример – составление каталога по алфавиту. Множество всех книг в библиотеке Х разбивается на конечное число классов – количество букв алфавита Y. Книги, начинающиеся с одной и той же буквы, принадлежат одному классу, и между любой парой таких книг существует отношение эквивалентности.

В то же время составляя каталог по алфавиту, мы осуществляем сюръективное отображение множества всех книг в библиотеке Х на множество букв алфавита Y.

Отношение эквивалентности – рефлексивно, симметрично и транзитивно. Эти свойства являются необходимыми и достаточными условиями разбиения множества на классы.

Отношение А на множестве М называется толерантностью, если оно рефлексивно и симметрично.

Так, отношение «быть знакомым» соответствует определению толерантности.

Отношение А на множестве Х называется отношением порядка, если оно транзитивно и антирефлексивно.

Отношение порядка характеризует соотношение объектов друг к другу по старшинству, по важности, оно не является симметричным. Отношение x
Множество, на котором задано отношение порядка, называется упорядоченным множеством. Понятие конечного упорядоченного множества совпадает с понятием конечной последовательности, состоящей из различных элементов. Простейшими примерами бесконечных упорядоченных множеств является множество всех целых чисел, множество рациональных чисел.

Заметим, что одно и то же множество можно упорядочить многими различными способами. Так, например, натуральные числа можно упорядочить «естественным образом»: 1, 2, 3, 4, ... Это же множество можно упорядочить так, что отдельно нечетные и отдельно четные числа расположены в порядке возрастания, а все нечетные числа считать предшествующими четным, т.е. 1, 3, 5, ... 2, 4, 6.

Биективное отображение «f» упорядоченного множества Х на упорядоченное множество Y называют соответствием подобия или подобным соответствием, если оно сохраняет порядок.

Два упорядоченных множества называются подобными, или имеющими один и тот же порядковый тип, если одно из них можно подобно отобразить на другое. Так, два конечных упорядоченных множества Х и Y, состоящих из одного и того же числа элементов, подобны между собой. Указанное выше биективное отображение между всей числовой прямой и интервалом (а,b) является соответствием подобия, и указанные множества подобны (рис. 1.1.9).

Заметим, что подобные множества имеют одну ту же мощность.

Упорядоченное множество называется вполне упорядоченным, если каждое его непустое подмножество содержит первый элемент. Так, все конечные упорядоченные множества – вполне упорядочены. Примером бесконечного вполне упорядоченного множества является множество всех натуральных чисел.