Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
Таким образом, с вероятностью 36,8% можно утверждать, что объем строительно-монтажных работ в октябре возрастет по сравнению с сентябрем.3.7. Оценка точности и надежности прогнозовВажным этапом прогнозирования социально-экономических явлений является оценка точности и надежности прогнозов. Эмпирической мерой точности прогноза, служит величина его ошибки, которая определяется как разность между прогнозными ( 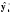 ) и фактическими (уt) значениями исследуемого показателя. Данный подход возможен только в двух случаях: ) и фактическими (уt) значениями исследуемого показателя. Данный подход возможен только в двух случаях:а) период упреждения известен, уже закончился, и исследователь располагает необходимыми фактическими значениями прогнозируемого показателя; б) строится ретроспективный прогноз, то есть рассчитываются прогнозные значения показателя для периода времени, за который уже имеются фактические значения. Это делается с целью проверки разработанной методики прогнозирования. В данном случае вся имеющаяся информация делится на две части в соотношении 2/3 к 1/3. Одна часть информации (первые 2/3 от исходного временного ряда) служит для оценивания параметров модели прогноза. Вторая часть информации (последняя 1/3 части исходного ряда) служит для реализации оценок прогноза. Полученные таким образом ретроспективно ошибки прогноза в некоторой степени характеризуют точность предлагаемой и реализуемой методики прогнозирования. Однако величина ошибки ретроспективного прогноза не может в полной мере и окончательно характеризовать используемый метод прогнозирования, так как она рассчитана только для 2/3 имеющихся данных, а не по всему временному ряду. В случае если, ретроспективное прогнозирование осуществляется по связным и многомерным динамическим рядам, то точность прогноза, соответственно, будет зависеть от точности определения значений факторных признаков, включенных в многофакторную динамическую модель, на всем периоде упреждения. При этом, возможны следующие подходы к прогнозированию по связным временным рядам: можно использовать как фактические, так и прогнозные значения признаков. Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:
Аналитические показатели точности прогноза позволяют количественно определить величину ошибки прогноза. К ним относятся: Абсолютная ошибка прогноза (*) определяется как разность между эмпирическими и прогнозными значениями признака и вычисляется по формуле: 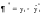 , (3.54) , (3.54)где: уt – фактическое значение признака; 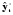 – прогнозное значение признака. – прогнозное значение признака.Относительная ошибка прогноза (d*отн) может быть определена как отношение абсолютной ошибки прогноза (*):
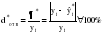 (3.55) (3.55)
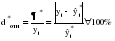 (3.56) (3.56)Абсолютная и относительная ошибки прогноза являются оценкой проверки точности единичного прогноза, что снижает их значимость в оценке точности всей прогнозной модели, так как изучаемое социально-экономическое явление подвержено влиянию различных факторов внешнего и внутреннего свойства. Единично удовлетворительный прогноз может быть получен и на базе реализации слабо обусловленной и недостаточно адекватной прогнозной модели и наоборот – можно получить большую ошибку прогноза по достаточно хорошо аппроксимирующей модели. Поэтому на практике иногда определяют не ошибку прогноза, а некоторый коэффициент качества прогноза (Кк), который показывает соотношение между числом совпавших (с) и общим числом совпавших (с) и несовпавших (н) прогнозов и определяется по формуле: 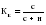 . (3.57) . (3.57)Значение Кк = 1 означает, что имеет место полное совпадение значений прогнозных и фактических значений и модель на 100% описывает изучаемое явление. Данный показатель оценивает удовлетворительный вес совпавших прогнозных значений в целом по временному ряду и изменяется в пределах от 0 до 1. Следовательно, оценку точности получаемых прогнозных моделей целесообразно проводить по совокупности сопоставлений прогнозных и фактических значений изучаемых признаков. Средним показателем точности прогноза является средняя абсолютная ошибка прогноза ( 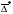 ), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида: ), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида: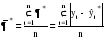 , (3.58) , (3.58)где: n – длина временного ряда. Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака. Для оценки точности прогноза используется средняя квадратическая ошибка прогноза, определяемая по формуле: 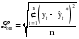 . (3.59) . (3.59)Размерность средней квадратической ошибки прогноза также соответствует размерности изучаемого признака. Между средней абсолютной и средней квадратической ошибками прогноза существует следующее примерное соотношение: 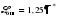 . (3.60) . (3.60)Недостатками средней абсолютной и средней квадратической ошибок прогноза является их существенная зависимость от масштаба измерения уровней изучаемых социально-экономических явлений. Поэтому на практике в качестве характеристики точности прогноза определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле вида: 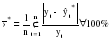 . (3.61) . (3.61)Данный показатель является относительным показателем точности прогноза и не отражает размерность изучаемых признаков, выражается в процентах и на практике используется для сравнения точности прогнозов полученных как по различным моделям, так и по различным объектам. Интерпретация оценки точности прогноза на основе данного показателя представлена в следующей таблице:
В качестве сравнительного показателя точности прогноза используется коэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле: 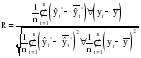 , (3.62) , (3.62)где: 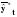 – средний уровень ряда динамики прогнозных оценок. – средний уровень ряда динамики прогнозных оценок.Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака. Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться в различных модификациях:
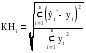 . (3.63) . (3.63)КН = 0, если 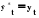 , то есть полное совпадение фактических и прогнозных значений признака. , то есть полное совпадение фактических и прогнозных значений признака.КН = 1, если при прогнозировании получают среднюю квадратическую ошибку адекватную по величине ошибке, полученной одним из простейших методов экстраполяции неизменности абсолютных цепных приростов. КН > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент несоответствия не имеет. 2. Коэффициент несоответствия (КН2), определяется как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от среднего уровня исходного временного ряда за весь рассматриваемый период: 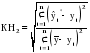 , (3.64) , (3.64)где: 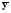 – средний уровень исходного ряда динамики. – средний уровень исходного ряда динамики.3. Коэффициент несоответствия (КН3), определяемый как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от теоретических, выравненных по уравнению тренда: 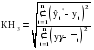 , (3.65) , (3.65)где: 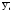 – теоретические уровни временного ряда, полученные по модели тренда. – теоретические уровни временного ряда, полученные по модели тренда.Контрольные вопросы к разделу III 1. Охарактеризуйте статистическое прогнозирование как составную часть общей теории прогностики. 2. Сформулируйте задачи статистического прогнозирования. 3. Дайте понятие объекта прогнозирования. 4. Перечислите основные понятия и термины, употребляемые в экономической прогностике.
8. Как осуществляется предварительный анализ рядов динамики? 9. Раскройте содержание понятия объективизации прогнозов. 10. Перечислите простейшие методы прогнозирования динамики. Раскройте их сущность. 11. Охарактеризуйте метод прогнозирования на основе экстраполяции трендов. 12. Охарактеризуйте методы прогнозирования на основе кривых роста. 13. Охарактеризуйте метод простого экспоненциального сглаживания. 14. Охарактеризуйте метод гармонических весов. 15. Как достигается точность и надежность прогнозов на основе рядов динамики? Глоссарий
Классификация статистических моделей:
Классификация прогнозов:
Этапы анализа:
Список рекомендуемой литературы Основная литература
Дополнительная литература
Заключение В предложенном учебном пособии рассмотрена методология комплексной оценки и анализа реальных социально-экономических явлений и процессов, представленных одномерными и многомерными временными рядами, в разрезе выявления, характеристики и моделирования тенденции и методов ее прогнозирования с учетом особенностей и специфики применяемых методов и изучаемого объекта исследования. Статистическая методология анализа временных рядов и прогнозирования находит широкое применение во многих областях знаний как на макро-, так и на микроуровнях экономического развития, оценке эффективности, финансового состояния и финансовой устойчивости, деловой активности сегментов различных рынков и организационно-правовых структур. Наиболее эффективным и целесообразным является широкое использование прикладного программного обеспечения при решении задач исследования конкретных социально-экономических явлений и процессов, что существенно ускоряет проведение расчетов. В этой связи распространены следующие программные продукты, такие как стандартные пакеты прикладных программ STATISTIKA, ОЛИМП, SPSS, STATGRAPHICS и другие. Руководство по изучению дисциплины (подготовлено д.э.н. профессором Садовниковой Н.А.) 1. Цели, задачи изучения дисциплины и сферы профессионального применения Современный этап социально-экономического развития страны выдвигает на первый план задачу оценки состояния и перспектив развития субъектов рыночных отношений на различных иерархических уровнях управления с целью выбора оптимальных управленческих, организационно-правовых и производственно-хозяйственных решений, направленных на повышение эффективности и деловой активности их функционирования и взаимодействия как в границах внутренней, так и внешней среды. В этой связи возрастает роль методологии статистического оценивания состояния, основных тенденций и перспектив развития субъектов рыночных отношений – организационно-правовых структур вне зависимости от отраслевой принадлежности, форм собственности и внутренней структурной градации, то есть возрастает роль анализа числовой информации, представленной в формах статистической, бухгалтерской и других видах отчетности и прогнозирования числовых параметров деятельности фирм, коммерческских банков, страховых компаний, различных сегментов финансового и других рынков с целью определения перспектив их развития и путей принятия наиболее эффективных решений и направлений дальнейшей деятельности. Дисциплина «Анализ временных рядов и прогнозирование» включает в себя комплексную методологию статистического анализа, моделирования и прогнозирования динамической информации, представленной временными рядами социально-экономических явлений и процессов. В курсе нашло отражение обобщение отечественного и зарубежного опыта использования статистико-математических методов изучения и прогнозирования социально-экономических явлений и процессов. Преподавание дисциплины «Анализ временных рядов и прогнозирование» строится исходя из требуемого уровня базовой подготовки экономистов по различным специальностям. Конечной целью изучения дисциплины является формирование у будущих специалистов глубоких теоретических знаний методологии и методики анализа временных рядов, статистического моделирования и прогнозирования, и практических навыков по экономико-статистическому анализу состояния и прогнозирования конкретных социально-экономических явлений и процессов на основе построения адекватных, и в достаточной степени аппроксимирующих реальные явления и процессы прогностических моделей, на основе которых возможна выработка конкретных предложений, рекомендаций и путей их прикладного использования на макро- и микро-уровнях. Роль и место дисциплины в профессиональной подготовке экономистов-статистиков определяется ее значительностью в изучении студентами специальных дисциплин. Поэтому, для успешного овладения ею требуется предварительное изучение таких дисциплин как «Теория статистики», «Экономическая информатика и вычислительная техника» и других дисциплин. В ходе изучения дисциплины ставятся задачи научить студентов:
Полученные знания являются неотъемлемой составляющей образования современного высококвалифицированного экономиста-аналитика, статистика, маркетолога, менеджера. Сфера профессионального применения полученных знаний обширна:
2. Необходимый объем знаний для изучения данной дисциплины Для успешного изучения данной дисциплины студент должен: Знать:
Уметь:
Иметь представление:
3. Перечень основных тем |

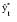 )
)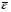 ,%
,%