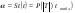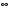Анализ временных рядов и прогнозирование. Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики

• Название: Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики
• Анкор: Анализ временных рядов и прогнозирование.doc
• Дата: 18.03.2017
• Размер: 2.56 Mb.
• Имя файла: Анализ временных рядов и прогнозирование.doc
• Тип: Учебно-методический комплекс; #3911
• страница: 19 из 23

Тема 1. Методологические аспекты анализа
и моделирования временных рядов
На основе данных приложения №1 Вашего варианта (по одному ряду динамики) необходимо сделать следующее:

1. 
   Охарактеризовать временной ряд в соответствии с существующей классификацией.
   
2. 
   Рассчитать и проанализировать следующие абсолютные, относительные и средние показатели временного ряда:
   

• 
  абсолютные приросты (цепные и базисные),
  
• 
  темпы роста (цепные и базисные),
  
• 
  темпы прироста (цепные и базисные)
  
• 
  абсолютное значение одного процента прироста,
  
• 
  средний уровень временного ряда,
  
• 
  средний абсолютный прирост,
  
• 
  средний темп роста,
  
• 
  средний темп прироста.
  

3. 
   На основе анализа полученных в п.2 показателей охарактеризовать характер основной тенденции в исследуемом временном ряду. Сформулируйте предположение о форме тренда.
   

Тема 2. Моделирование основной тенденции
временного ряда
На основе данных приложения № 1 Вашего варианта (по одному ряду динамики) необходимо сделать следующее:

1. 
   Определите наличие основной тенденции развития в исследуемом ряду на основе кумулятивного Т-критерия.
   
2. 
   Определите вид тенденции (средней и дисперсии) в исследуемом ряду динамики методом сравнения средних уровней временного ряда.
   
3. 
   Определите вид тенденции (средней и дисперсии) в исследуемом ряду динамики методом методом Фостера-Стюарта.
   
4. 
   Определите характер основной тенденции в исследуемом ряду динамики методом Кокса-Стюарта.
   
5. 
   Проанализируйте характер основной тенденции временного ряда методом скользящей средней. Обоснуйте выбор порядка скольжения.
   
6. 
   Определите аналитическую форму выражения основной тенденции исследуемого временного ряда по любому рациональному многочлену (линейной функции и параболе второго порядка).
   
7. 
   Выберите и обоснуйте модель на основе:
   

• 
  графического метода;
  
• 
  метода последовательных разностей.
  

8. 
   Определите параметры выбранной функции на основе метода наименьших квадратов.
   
9. 
   Проверьте правильность выбранного уравнения тренда на основе:
   

• 
  минимизации сумм квадратов отклонений эмпирических значений признака от теоретических, полученных по уравнению тренда;
  
• 
  средней квадратической ошибки;
  
• 
  средней ошибки аппроксимации;
  
• 
  дисперсионного метода анализа;
  
• 
  критерия серий, основанного на медиане выборки.
  

Тема 3. Моделирование случайной компоненты временного ряда
По данным Вашего варианта и на основе полученного в теме 1 уравнения тренда необходимо произвести следующее:

1. 
   Определить отклонения теоретических значений признака, полученных по уравнению тренда от эмпирических значений признака.
   
2. 
   Определить наличие случайного компонента в исследуемом временном ряду на основе критериев:
   

• 
  серий, основанного на медиане выборки;
  
• 
  «восходящих» и «нисходящих» серий;
  
• 
  «минимума» и «максимума».
  

Тема 4. Моделирование периодической компоненты
временного ряда
По данным любого статистического ежегодника или Интернет-ресурсов подберите временной ряд помесячных данных за полный год (12 месяцев).

1. 
   Изобразите графически исходные данные и произведите визуальный анализ.
   
2. 
   Проверьте исходный временной ряд на наличие тенденции любым известным Вам методом.
   
3. 
   Проверьте временной ряд на наличие сезонной компоненты с помощью:
   

• 
  дисперсионного анализа;
  
• 
  критерия «пиков» и «ям».
  

4. 
   Выберите и обоснуйте модель тренда. Рассчитайте параметры уравнения тренда и определите теоретические уровни ряда по трендовой модели.
   
5. 
   Определите абсолютные и относительные отклонения эмпирических значений уровней временного ряда от теоретических, полученных по уравнению тренда. Нанесите эти отклонения на график и проанализируйте амплитуду их изменений.
   
6. 
   Проверьте абсолютные и относительные отклонения фактических уровней от выровненных на наличие автокорреляции любым известным Вам способом.
   
7. 
   Постройте модель сезонной волны по отклонениям эмпирических значений уровней временного ряда от выровненных по тренду методом гармонического анализа.
   
8. 
   Определите гармонику Фурье, наилучшим образом отражающую периодичность изменения уровней временного ряда на основе средней квадратической ошибки.
   
9. 
   По полученной в п. 8 модели сезонной волны сделайте прогноз на 2-3 периода упреждения
   

Тема 5. Моделирование связных временных рядов
По данным Приложения 2 необходимо построить модель связных временных рядов.

1. 
   Определить результативный и факторный признаки.
   
2. 
   Постройте график зависимости результативного признака с каждым из факторных.
   
3. 
   Проверьте временные ряды на наличие автокорреляции в уровнях на основе известных Вам критериев.
   
4. 
   Постройте модели авторегрессионных преобразований методами:
   

• 
  последовательных разностей;
  
• 
  конечных разностей;
  
• 
  по отклонениям эмпирических значений признаков от выравненных по тренду;
  
• 
  Фриша-Воу.
  

5. Проверьте временные ряды на наличие автокорреляции в остатках на основе коэффициента автокорреляции, критерия Дарбина-Уотсона и других критериев.

6. Проверьте адекватность построенной в п.4 модели исследуемому процессу на основе:

• 
  средней ошибки аппроксимации;
  
• 
  средней квадратической ошибки.
  

7. 
   Сформулируйте выводы.
   

Тема 6. Прогнозирование динамики социально-экономических явлений
Задание 6.1. Простейшие методы прогнозной экстраполяции
На основе данных приложения № 1 Вашего варианта (по одному ряду динамики) необходимо сделать следующее:

1. 
   Построить прогноз методами:
   

• 
  среднего абсолютного прироста;
  
• 
  среднего темпа роста.
  

Обосновать выбор метода прогнозирования, предварительно проверив предпосылки их реализации.

2. 
   Произвести оценку точности полученных прогнозов на основе:
   

• 
  средней квадратической ошибки;
  
• 
  коэффициента несоответствия.
  

Задание 6.2. Прогнозирование на основе кривых роста
На основе данных приложения № 1 Вашего варианта (по одному ряду динамики) необходимо сделать следующее:

1. 
   Произвести прогноз на 2-3 периода упреждения на основе кривой роста Гомперца.
   
2. 
   Произвести прогноз на 2-3 периода упреждения на основе кривой роста Перля-Рида.
   
3. 
   Произвести оценку точности полученных прогнозов на основе:
   

• 
  средней квадратической ошибки;
  
• 
  коэффициента несоответствия
  

Задание 6.3. Прогнозирование с учетом дисконтирования информации
По данным приложения 1 необходимо выполнить следующее:

1. 
   Проверить и обосновать предпосылки реализации методов простого экспоненциального сглаживания и гармонических весов на основе графического метода анализа.
   
2. 
   Произвести прогноз на 2-3 периода упреждения методом простого экспоненциального сглаживания.
   
3. 
   Произвести прогноз на 2-3 периода упреждения методом гармонических весов.
   
4. 
   Произвести оценку точности полученных в пп.2 и 3 прогнозов на основе:
   

• 
  средней квадратической ошибки;
  
• 
  коэффициента несоответствия.
  

Задание 6.4. Прогнозирование рядов динамики, не имеющих тенденции

1. 
   По данным любого статистического ежегодника или периодической печати необходимо отобрать одномерный временной ряд абсолютных величин не менее, чем 10 уровней.
   
2. 
   На основе графического анализа сделать вывод о наличии или отсутствии тенденции в исходном временном ряду.
   
3. 
   Любым известным методом определить отсутствие тенденции в исследуемом временном ряду.
   
4. 
   На основе распределения Пуассона определить вероятность совершения или несовершения благоприятной тенденции.
   

Тема 7. Прогнозирование многомерных
временных рядов
На основе данных приложения 2 необходимо построить многофакторную динамическую модель взаимосвязи по отобранным признакам. Для этого необходимо:

1. 
   Определить результативный и факторный признаки.
   
2. 
   Проверить ряды динамики на наличие автокорреляции.
   
3. 
   Для каждого года построить матрицы парных коэффициентов корреляции. Проанализировать матрицу полученных коэффициентов.
   
4. 
   Выбрать вид модели взаимосвязи.
   
5. 
   Построить статические модели за каждый год по данным Вашего варианта.
   
6. 
   Проверить значимость полученных уравнений и коэффициентов регрессии. Сделайте выводы.
   
7. 
   Произвести сглаживание коэффициентов регрессии и факторных признаков для выявления тенденции их изменения.
   
8. 
   Построить прогнозы для коэффициентов регрессии и факторных признаков методом экстраполяции тренда.
   
9. 
   Построить прогноз на основе многофакторной динамической модели.
   
10. 
    Оценить точность полученного прогноза.
    

Приложения

Приложение 1
Таблица 1

Динамика числа проданных квартир в одном из регионов
Российской Федерации за период 1996-2008 гг. (данные условные)

Год	Число проданных квартир, тыс.ед.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	18,27 17,99 19,51 25,37 24,38 23,86 36,42 39,05 42,15 47,67 50,10 50,78 52,00

Таблица 2

Динамика объема строительно-монтажных работ, выполненных собственными силами одной из строительных организаций города за период 1996-2008 гг. (данные условные)

Год	Объем строительно-монтажных работ, выполненных собственными силами, млн.руб.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	32,5 35,7 35,4 38,4 37,6 51,0 50,8 66,5 77,9 97,8 97,9 98,3 98,5

Таблица 3

Динамика среднегодовой численности промышленно-производственного персонала промышленности Российской
Федерации, млн. чел. (данные условные)

Год	Среднегодовая численность промышленно-производственного персонала, млн. чел.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	20,0 19,3 17,4 16,0 14,9 14,0 13,1 13,0 13,0 13,1 13,2 12,8 12,7

Таблица 4

Динамика прибыли одного из предприятий города

за период 1996-2008 гг. (данные условные)

Год	Прибыль, млн. руб.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	48,11 44,44 41,53 38,10 38,22 39,81 38,26 40,17 41,54 43,65 45,66 50,11 52,15

Таблица 5

Динамика численности безработных, зарегистрированных в органах государственной службы занятости в одном из регионов Российской Федерации (данные условные)

Год	Численность безработных, млн.чел.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	0,61 0,75 0,84 0,96 1,18 1,31 1,71 1,91 1,89 2,11 2,10 2,13 2,15

Таблица 6

Динамика сброса загрязненных сточных вод
в Российской Федерации (данные условные)

Год	Сброс загрязненных сточных вод, млрд.куб.м.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	28,2 26,7 25,1 25,0 24,9 23,8 22,9 21,1 20,7 20,0 19,8 19,9 19,5

Таблица 7

Динамика выбросов загрязняющих веществ в атмосферный воздух от стационарных источников

(данные условные)

Год	Выбросов загрязняющих веществ в атмосферный воздух от стационарных источников, млн.т.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	29,1 27,4 23,2 22,8 22,3 21,1 19,8 18,5 18,8 18,0 18,1 18,0 17,7

Таблица 8

Динамика жилищного фонда Российской Федерации

(данные условные)

Год	Жилищный фонд, млрд.кв.м.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	2,511 2,612 2,687 2,698 2,711 2,723 2,739 2,774 2,799 2,811 2,807 2,812 2,820

Таблица 9

Динамика числа семей, состоявших на учете на получение жилья

(данные условные)

Год	Число семей, состоявших на учете на получение жилья, млн.ед.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	9,6 9,2 8,4 7,7 7,2 6,7 6,2 5,8 5,3 5,2 5,4 5,1 5,0

Таблица 10

Динамика числа проданных квартир

(данные условные)

Год	Число проданных квартир, тыс.ед.
1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008	7,3 8,1 14,5 26,4 29,9 42,5 44,1 37,0 44,7 45,2 45,0 45,1 45,5

Приложение 2
Распределение Стьюдента (t – распределение)

v	Вероятность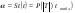
	0,9	0,8	0,7	0,5	0,4	0,3	0,2	0,1	0,05	0,02	0,01	0,001
1	0,158	0,325	0,510	1,000	1,376	1,963	3,078	6,314	12,706	31,821	63,657	636,619
2	0,142	0,289	0,445	0,816	1,061	1,386	1,886	2,920	4,303	6,965	9,925	31,598
3	0,137	0,277	0,424	0,765	0,978	1,250	1,638	2,353	3,182	4,541	5,841	12,941
4	0,134	0,271	0,414	0,741	0,941	1,190	1,563	2,132	2,776	3,747	4,604	8,610
5	0,132	0,267	0,406	0,727	0,920	1,156	1,476	2,015	2,571	3,365	4,043	6,859
6	0,131	0,265	0,404	0,718	0,906	1,134	1,440	1,943	2,447	3,143	3,707	5,959
7	0,130	0,263	0,402	0,711	0,896	1,119	1,415	1,895	2,365	2,998	3,499	5,405
8	0,130	0,262	0,399	0,706	0,889	1,108	1,397	1,860	2,306	2,896	3,355	5,041
9	0,129	0,261	0,398	0,703	0,883	1,100	1,383	1,833	2,262	2,821	3,250	4,781
10	0,129	0,260	0,327	0,700	0,879	1,093	1,372	1,812	2,228	2,764	3,169	4,583
11	0,129	0,260	0,396	0,697	0,976	1,088	1,363	1,796	2,201	2,718	3,106	4,437
12	0,128	0,259	0,395	0,695	0,873	1,083	1,356	1,782	2,179	2,681	3,055	4,318
13	0,128	0,259	0,394	0,694	0,870	1,079	1,350	1,771	2,160	2,650	3,012	4,221
14	0,128	0,258	0,393	0,692	0,888	1,076	1,345	1,761	2,145	2,624	2,977	4,140
15	0,128	0,258	0,393	0,691	0,866	1,074	1,341	1,753	2,131	2,602	2,947	4,073
16	0,128	0,258	0,392	0,690	0,865	1,071	1,337	1,746	2,120	2,583	2,921	4,015
17	0,128	0,257	0,392	0,689	0,863	1,069	1,333	1,740	2,110	2,567	2,898	3,965
18	0,127	0,257	0,392	0,688	0,862	1,067	1,330	1,734	2,101	2,552	2,878	3,922
19	0,127	0,257	0,391	0,688	0,861	1,066	1,326	1,789	2,093	2,539	2,861	3,833
20	0,127	0,257	0,391	0,687	0,860	1,064	1,325	1,725	2,066	2,528	2,845	3,850
21	0,127	0,257	0,391	0,686	0,859	1,063	1,323	1,721	2,080	2,518	2,831	3,819
22	0,127	0,256	0,390	0,686	0,858	1,061	1,321	1,717	2,074	2,508	2,819	3,792
23	0,127	0,256	0,390	0,685	0,868	1,060	1,319	1,714	2,069	2,500	2,807	3,767
24	0,127	0,256	0,390	0,685	0,857	1,059	1,318	1,711	2,064	2,402	2,797	3,745
25	0,127	0,256	0,390	0,684	0,856	1,058	1,316	1,708	2,060	2,485	2,787	3,725
26	0,127	0,256	0,390	0,684	0,856	1,058	1,315	1,706	2,056	2,479	2,779	3,707
27	0,127	0,256	0,389	0,684	0,855	1,057	1,314	1,703	2,052	2,473	2,771	3,690
28	0,127	0,256	0,389	0,683	0,855	1,056	1,313	1,701	2,048	2,467	2,763	3,674
29	0,127	0,256	0,389	0,683	0,854	1,055	1,311	1,699	2,045	2,462	2,756	3,659
30	0,127	0,256	0,389	0,683	0,854	1,055	1,310	1,697	2,042	2,457	2,750	3,646
40	0,126	0,255	0,388	0,681	0,851	1,050	1,303	1,684	2,021	2,423	2,704	3,551
60	0,126	0,254	0,387	0,679	0,848	1,046	1,296	1,671	2,000	2,390	2,660	3,460
120	0,126	0,254	0,386	0,677	0,845	1,041	1,289	1,658	1,980	2,358	2,617	3,373
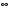
	0,126	0,253	0,385	0,674	0,842	1,036	1,282	1,645	1,960	2,326	2,576	3,291