Методы решения систем линейных алгебраических уравнений
 Скачать 151.49 Kb. Скачать 151.49 Kb.
|
Метод Якоби.Будем считать, что все диагональные элементы матрицы Aотличны от нуля, и перепишем систему (1), разрешая каждое уравнение относительно переменной, стоящей на диагонали: 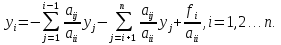 (2) (2)Выберем некоторое начальное приближение 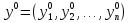 и построим последовательность векторов и построим последовательность векторов 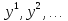 , вычисляя вектор , вычисляя вектор 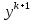 по уже найденному вектору по уже найденному вектору 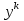 при помощи соотношений: при помощи соотношений: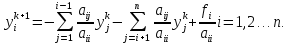 (3) (3)Формула (3) определяет итерационный метод решения системы (1), называемый методом Якоби. Теорема: Пусть матрица A — матрица с диагональным преобладанием. Тогда итерационный метод Якоби сходится при любом начальном приближении  . .Доказательство: Заметим, прежде всего, что условие диагонального преобладания означает, что 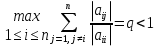 (4) (4)Пусть 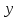 — решение системы уравнений(1). Здесь и всюду в дальнейшем погрешность метода на — решение системы уравнений(1). Здесь и всюду в дальнейшем погрешность метода на 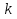 -том шаге итераций, т. е. вектор -том шаге итераций, т. е. вектор 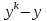 , будем обозначать через , будем обозначать через 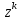 . Вычитая почленно из равенства (3) равенство (2), получим . Вычитая почленно из равенства (3) равенство (2), получим следовательно, 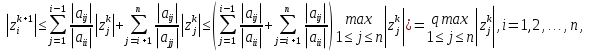 откуда вытекает, что 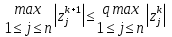 для любого 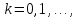 поэтому поэтому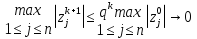 (5) (5)при 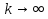 , поскольку , поскольку 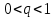 , а это означает, что , а это означает, что 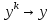 . .Оценка (5) показывает, что, чем меньше q, тем быстрее сходится метод простой итерации. Метод Якоби сходится при любом начальном приближении 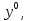 если матрица A – матрица с диагональным преобладанием. Необходимо убедиться, что исходная система уравнений имеет матрицу c диагональным преобладанием. Действительно, матрица системы (1) имеет вид: если матрица A – матрица с диагональным преобладанием. Необходимо убедиться, что исходная система уравнений имеет матрицу c диагональным преобладанием. Действительно, матрица системы (1) имеет вид: 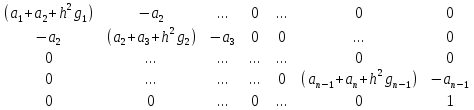 Результаты вычислений при 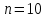 представлены далее: представлены далее: (максимальная погрешность выделена красным)
При нулевом начальном векторе данный метод сохраняет необходимую погрешность в виде h2 лишь до n=10. Это обусловлено особенностью конкретно заданной задачи, а также тем, что метод зависит от выбора начального приближения. При проведении экспериментов, выберем другое начальное приближение, чтобы получить более точное решение при большем разбиении отрезка. |
