Экспериментальная часть для метода Зейделя.
Эксперимент 1.
Зафиксируем значение eps=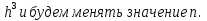
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
7
|
0,008
|
0,027449546
|
0,04
|
6
|
11
|
4,63E-03
|
0,021410118
|
0,027777778
|
7
|
15
|
0,002915452
|
0,020339777
|
0,020408163
|
8
|
20
|
0,001953125
|
0,018286454
|
0,015625
|
9
|
25
|
0,001371742
|
0,017808903
|
0,012345679
|
10
|
32
|
0,001
|
0,015895341
|
0,01
|
11
|
40
|
0,000751315
|
0,014314535
|
0,008264463
|
При n=11 заданная точность не достигается. Следовательно, дальше увеличивать n смысла нет.
Эксперимент 2.
Зафиксируем значение n = 20 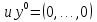 , будем изменять порядок eps пока не достигнем заданной точности. , будем изменять порядок eps пока не достигнем заданной точности.
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
20
|
39
|
0,0025
|
0,095724889
|
0,0025
|
20
|
151
|
0,000125
|
0,008331488
|
0,0025
|
20
|
262
|
0,00000625
|
0,004056509
|
0,0025
|
20
|
373
|
3,125E-07
|
0,003841901
|
0,0025
|
Мы видим, что при значении 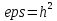 и n=20 заданная точность не достигается. Т.е. при n = 20, и n=20 заданная точность не достигается. Т.е. при n = 20, 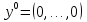 можно достичь точности можно достичь точности 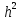 только при только при 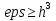 . .
Эксперимент 3.
Будем менять n при значении 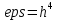
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
11
|
0,0016
|
0,016529239
|
0,04
|
10
|
53
|
0,0001
|
0,008334488
|
0,01
|
15
|
136
|
1,98E-05
|
0,005453436
|
0,004444444
|
20
|
262
|
0,00000625
|
0,004056509
|
0,0025
|
25
|
435
|
0,00000256
|
0,003221226
|
0,0016
|
30
|
656
|
1,23457E-06
|
0,002670273
|
0,001111111
|
Будем менять n при значении 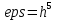
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
14
|
0,00032
|
0,014968555
|
0,04
|
10
|
74
|
0,00001
|
0,007566937
|
0,01
|
15
|
192
|
1,32E-06
|
0,005094404
|
0,004444444
|
20
|
373
|
3,125E-07
|
0,003841901
|
0,0025
|
25
|
622
|
1,02E-07
|
0,003081294
|
0,0016
|
30
|
941
|
4,11523E-08
|
0,002571331
|
0,001111111
|
Вывод: При достаточно больших n и 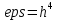 и и 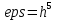 точность достигается (Если точность достигается при точность достигается (Если точность достигается при 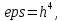 то при то при 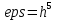 тем более точность достигается при тех же n). тем более точность достигается при тех же n).
Эксперимент 4.
Пусть начальный вектор  =(0,0, …,0) и eps= =(0,0, …,0) и eps=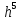 . Тогда: . Тогда:
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
14
|
0,00032
|
0,01482946
|
0,04
|
10
|
72
|
0,00001
|
0,007560197
|
0,01
|
15
|
186
|
1,32E-06
|
0,005094252
|
0,004444444
|
20
|
362
|
3,13E-07
|
0,003841958
|
0,0025
|
25
|
605
|
1,02E-07
|
0,003081313
|
0,0016
|
30
|
917
|
4,12E-08
|
0,002571326
|
0,001111111
|
Теперь возьмем вектор  = (0.05 ,…, 0.05). = (0.05 ,…, 0.05).
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
13
|
0,00032
|
0,014836832
|
0,04
|
10
|
68
|
0,00001
|
0,007560815
|
0,01
|
15
|
177
|
1,32E-06
|
0,005094617
|
0,004444444
|
20
|
347
|
3,13E-07
|
0,00384186
|
0,0025
|
25
|
581
|
1,02E-07
|
0,003081336
|
0,0016
|
30
|
882
|
4,12E-08
|
0,002571364
|
0,001111111
|
По сравнению с предыдущими результатами, при  = (0.05 ,…, 0.05), шагов итераций меньше при любых n начиная с n=10. = (0.05 ,…, 0.05), шагов итераций меньше при любых n начиная с n=10.
n
|
разность кол-ва итераций
|
5
|
0
|
10
|
2
|
15
|
6
|
20
|
11
|
25
|
17
|
30
|
24
|
Теперь возьмем вектор  = (0.1 ,…, 0.1). = (0.1 ,…, 0.1).
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
13
|
0,00032
|
0,014836832
|
0,04
|
10
|
68
|
0,00001
|
0,007560815
|
0,01
|
15
|
177
|
1,32E-06
|
0,005094617
|
0,004444444
|
20
|
347
|
3,13E-07
|
0,00384186
|
0,0025
|
25
|
581
|
1,02E-07
|
0,003081336
|
0,0016
|
30
|
882
|
4,12E-08
|
0,002571364
|
0,001111111
|
В данном случае количество шагов продолжает уменьшаться. Сравним с предыдущими результатами:
n
|
разность кол-ва итераций
|
5
|
1
|
10
|
4
|
15
|
9
|
20
|
15
|
25
|
24
|
30
|
35
|
Возьмем в качестве начального вектора вектор  =(b[1]/A[1][1], …, b[n]/A[n][n]) при eps= =(b[1]/A[1][1], …, b[n]/A[n][n]) при eps=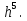
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
14
|
0,00032
|
0,014845898
|
0,04
|
10
|
74
|
0,00001
|
0,007561944
|
0,01
|
15
|
192
|
1,32E-06
|
0,005093746
|
0,004444444
|
20
|
373
|
3,13E-07
|
0,003841742
|
0,0025
|
25
|
621
|
1,02E-07
|
0,003081343
|
0,0016
|
30
|
940
|
4,11523E-08
|
0,002571351
|
0,001111111
|
 В данном случае результаты количества итераций увеличиваются. В данном случае результаты количества итераций увеличиваются.
|
 Скачать 151.49 Kb.
Скачать 151.49 Kb.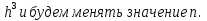
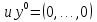 , будем изменять порядок eps пока не достигнем заданной точности.
, будем изменять порядок eps пока не достигнем заданной точности.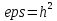 и n=20 заданная точность не достигается. Т.е. при n = 20,
и n=20 заданная точность не достигается. Т.е. при n = 20, 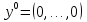 можно достичь точности
можно достичь точности 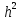 только при
только при 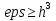 .
.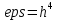
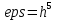
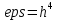 и
и 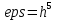 точность достигается (Если точность достигается при
точность достигается (Если точность достигается при 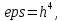 то при
то при 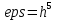 тем более точность достигается при тех же n).
тем более точность достигается при тех же n). =(0,0, …,0) и eps=
=(0,0, …,0) и eps=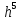 . Тогда:
. Тогда: = (0.05 ,…, 0.05).
= (0.05 ,…, 0.05). = (0.05 ,…, 0.05), шагов итераций меньше при любых n начиная с n=10.
= (0.05 ,…, 0.05), шагов итераций меньше при любых n начиная с n=10.  = (0.1 ,…, 0.1).
= (0.1 ,…, 0.1). =(b[1]/A[1][1], …, b[n]/A[n][n]) при eps=
=(b[1]/A[1][1], …, b[n]/A[n][n]) при eps=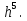
 В данном случае результаты количества итераций увеличиваются.
В данном случае результаты количества итераций увеличиваются.