Методы решения систем линейных алгебраических уравнений
 Скачать 151.49 Kb. Скачать 151.49 Kb.
|
Метод наискорейшего спуска.Рассмотрим следующий итерационный метод: 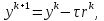 (15) (15)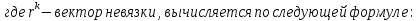 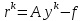 , , 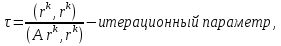 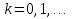 . .Метод (15) называется методом наискорейшего спуска. Теорема: Пусть матрица 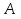 симметрична и положительно определена. Тогда метод (15) сходится при любом начальном приближении. Справедлива следующая оценка скорости сходимости: симметрична и положительно определена. Тогда метод (15) сходится при любом начальном приближении. Справедлива следующая оценка скорости сходимости: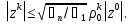 (16) (16)Замечание: Оценка (16) показывает, что погрешность метода (15) убывает с той же скоростью, что и погрешность метода простой итерации при оптимальном выборе параметра τ. Доказательство: Пусть 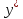 — решение задачи, то есть A — решение задачи, то есть A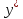 = b. Используя симметрию матрицы = b. Используя симметрию матрицы 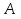 , получим , получим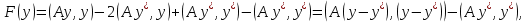 (17) (17)откуда вследствие положительной определенности матрицы 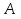 вытекает, что единственной точкой минимума функционала вытекает, что единственной точкой минимума функционала 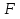 является является 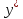 . .Используя (15) и зная, что 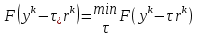 , ,получим: 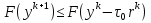 , где , где 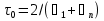 , откуда вследствие представления (17) вытекает, что , откуда вследствие представления (17) вытекает, что 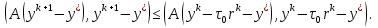 Заметим теперь, что 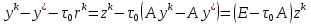 , ,следовательно, 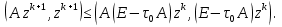 Представляя вектор 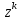 в виде разложения по ортонормированному базису собственных векторов матрицы в виде разложения по ортонормированному базису собственных векторов матрицы 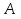 , получим: , получим: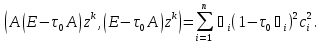 Как установлено 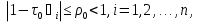 следовательно, 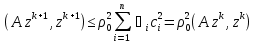 , , откуда, очевидно, вытекает неравенство 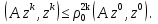 Используя теперь оценки 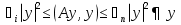 , получим: , получим: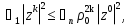 а это эквивалентно оценки (16). а это эквивалентно оценки (16).Метод наискорейшего спуска сходится при любом начальном приближении 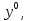 если матрица если матрица 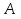 – симметрична и положительно определена. Необходимо убедиться, что исходная система уравнений имеет симметричную и положительно определенную матрицу. Действительно, матрица системы (1) имеет вид: – симметрична и положительно определена. Необходимо убедиться, что исходная система уравнений имеет симметричную и положительно определенную матрицу. Действительно, матрица системы (1) имеет вид: 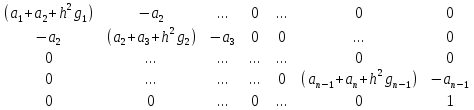 Матрица A называется положительно определённой, если для всех 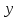 ≠0, ≠0,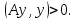 Действительно, Действительно, 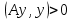 : : 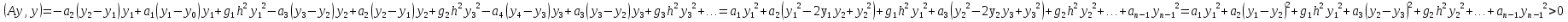 Результаты вычислений при 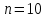 представлены далее: представлены далее: (максимальная погрешность выделена красным)
Наблюдаем достаточную точность, как и в предыдущих методах.
|
