Методы решения систем линейных алгебраических уравнений
 Скачать 151.49 Kb. Скачать 151.49 Kb.
|
Метод Зейделя.Формулы (1.2) допускают естественную модификацию. Именно, при вычислении 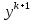 будем использовать уже найденные компоненты вектора x будем использовать уже найденные компоненты вектора x 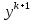 , т. е. , т. е. 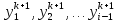 . В результате приходим к итерационному методу Зейделя: . В результате приходим к итерационному методу Зейделя: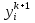 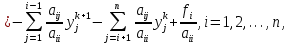 k = 0, 1, . . ., k = 0, 1, . . ., Метод Зейделя позволяет более экономно расходовать память, поскольку в данном случае вновь получаемые компоненты вектора 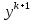 можно размещать на месте соответствующих компонент вектора можно размещать на месте соответствующих компонент вектора 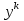 , в то время как при реализации метода Якоби все компоненты векторов , в то время как при реализации метода Якоби все компоненты векторов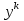 , , 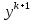 должны одновременно находиться в памяти компьютера. Достаточное условие сходимости и оценку скорости сходимости метода Зейделя дает должны одновременно находиться в памяти компьютера. Достаточное условие сходимости и оценку скорости сходимости метода Зейделя дает Теорема 1.2. Пусть матрица A — матрица с диагональным преобладанием. Тогда метод Зейделя сходится при любом начальном приближении  ; справедлива оценка скорости сходимости: ; справедлива оценка скорости сходимости: 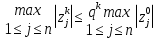 (1.6) (1.6) Доказательство. Вычитая почленно из равенства (6.2) равенство (1.1), получим 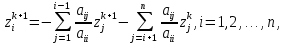 (1.7) (1.7)Пусть 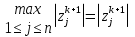 |. Из l-того уравнения системы (1.7) вытекает, что |. Из l-того уравнения системы (1.7) вытекает, что 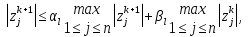 где 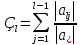 , , 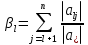 , ,следовательно, 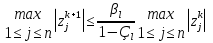 . .Из условия (1.3) получаем, что 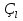 + +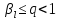 , но тогда и , но тогда и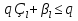 , таким образом, , таким образом, 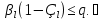 Результаты вычислений при 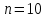 представлены далее: представлены далее: (максимальная погрешность выделена красным)
Уже сейчас можно заметить более высокую точность метода Зейделя в сравнении с методом Якоби. Видно, насколько близко приближается метод к точному решению.
Метод Зейделя сохраняет устойчивость до n=31. Далее погрешность превышает точность h2. |
