Методы решения систем линейных алгебраических уравнений
 Скачать 151.49 Kb. Скачать 151.49 Kb.
|
Метод релаксации.Рассмотрим итерационный процесс: 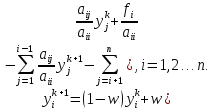 (7) (7)Этот метод называется методом релаксации, число w – релаксационный параметр. В случае нижней релаксации 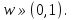 Мы исследуем сходимость метода релаксации в случае, когда матрица  симметрична и положительно определена. С этой целью перепишем его в матричном виде. Обозначим через симметрична и положительно определена. С этой целью перепишем его в матричном виде. Обозначим через  нижнюю треугольную матрицу с нулевой главной диагональю; элементы, стоящие под главной диагональю матрицы нижнюю треугольную матрицу с нулевой главной диагональю; элементы, стоящие под главной диагональю матрицы 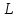 , совпадают с соответствующими элементами матрицы , совпадают с соответствующими элементами матрицы 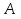 . Через . Через 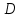 обозначим диагональную матрицу, на диагонали которой стоят диагональные элементы матрицы обозначим диагональную матрицу, на диагонали которой стоят диагональные элементы матрицы 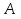 . Понятно, что . Понятно, что 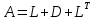 . Нетрудно убедиться, что равенства (7) с учетом введенных обозначений принимают вид: . Нетрудно убедиться, что равенства (7) с учетом введенных обозначений принимают вид: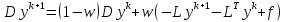 После элементарных преобразований получим, что 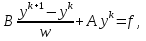 (8) (8)где 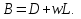 Нам потребуется следующая общая теорема, полезная при исследовании многих итерационных методов. Теорема: Пусть матрица 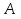 симметрична и положительно определена. Тогда итерационный метод симметрична и положительно определена. Тогда итерационный метод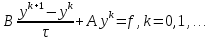 (9) (9)где 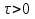 , сходится при любом начальном приближении , сходится при любом начальном приближении  , если , если 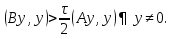 (10) (10)Доказательство: Если 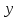 – решение, то, очевидно, – решение, то, очевидно,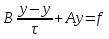 (11) (11) Вычитая почленно из равенства (11) равенство (9), получим 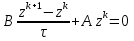 (12) (12)Используя тривиальное равенство 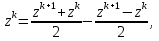 преобразуем (12) к виду 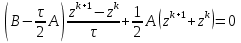 (13) (13)Умножим обе части равенства (13) скалярно на вектор 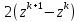 После элементарных преобразований с учетом симметрии матрицы 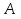 получим: получим: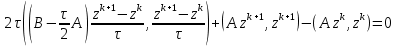 (14) (14)Вследствие условия (10) первое слагаемое в правой части (14) неотрицательно, поэтому 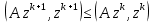 , т.е. числовая последовательность , т.е. числовая последовательность 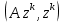 не возрастает. Кроме того, она ограничена снизу нулем, так как матрица не возрастает. Кроме того, она ограничена снизу нулем, так как матрица 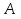 положительно определена. Таким образом, последовательность положительно определена. Таким образом, последовательность 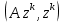 имеет предел. Отсюда вытекает, что имеет предел. Отсюда вытекает, что 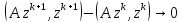 при при 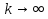 , следовательно, и , следовательно, и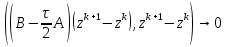 при при 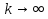 , ,а поскольку матрица 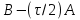 положительна определена (см. условие (10), то положительна определена (см. условие (10), то 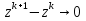 при при 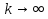 . Используя теперь уравнение (12) и невырожденность матрицы . Используя теперь уравнение (12) и невырожденность матрицы 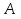 , получим, что , получим, что 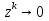 при при 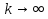 . .С использованием теоремы просто доказывается. Теорема: Пусть матрица 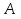 положительно определена, параметр релаксации удовлетворяет условию: 0 < ω < 2. Тогда метод релаксации сходится при любом начальном приближении положительно определена, параметр релаксации удовлетворяет условию: 0 < ω < 2. Тогда метод релаксации сходится при любом начальном приближении  . .Доказательство: Покажем, что при сделанных предположениях выполнено условие (10) при 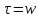 , , 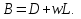 Действительно, Действительно,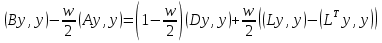 , ,но все диагональные элементы положительно определенной матрицы положительны, поэтому 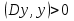 при при 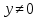 , а , а 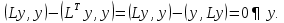 Метод релаксации сходится при любом начальном приближении  , если матрица А – положительно определена и параметр релаксации удовлетворяет условию: 0< , если матрица А – положительно определена и параметр релаксации удовлетворяет условию: 0<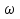 <2. Необходимо убедиться, что исходная система уравнений имеет положительно определённую матрицу. <2. Необходимо убедиться, что исходная система уравнений имеет положительно определённую матрицу.Матрица A называется положительно определённой, если для всех 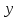 ≠0, ≠0,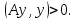 Действительно, Действительно, 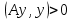 : : 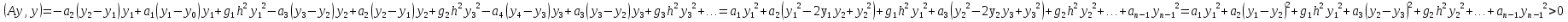 Результаты вычислений при 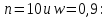
При данном параметре  метод показывает приемлемую точность. метод показывает приемлемую точность. Построим график 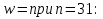 Заметна более высокая точность при разбиении отрезка на большее количество частей. |
