Более точное решение, которое практически накладывается на точное.
Другие эксперименты. Экспериментальная часть для метода Якоби.
Эксперимент 1.
1.1 Зафиксируем значение eps=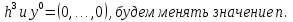
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
10
|
0,008
|
0,038836019
|
0,04
|
6
|
14
|
0,00462963
|
0,040036738
|
0,027777778
|
7
|
21
|
0,002915452
|
0,033625109
|
0,020408163
|
8
|
29
|
0,001953125
|
0,029840483
|
0,015625
|
9
|
38
|
0,001371742
|
0,027583694
|
0,012345679
|
10
|
49
|
0,001
|
0,024749754
|
0,01
|
11
|
61
|
0,000751315
|
0,023142206
|
0,008264463
|
При n≥11 заданная точность не достигается.
Исходя из того, что метод Якоби чувствителен к значениям вектора начального приближения, проведем этот эксперимент с другим начальным приближением. Что при определенных значениях даст нам уменьшение погрешности при n≥11.
1.2 Зафиксируем значение eps=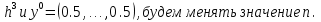
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
12
|
0,008
|
0,009662575
|
0,04
|
6
|
23
|
0,00462963
|
0,002809168
|
0,027777778
|
7
|
27
|
0,002915452
|
0,007521441
|
0,020408163
|
8
|
44
|
0,001953125
|
0,001536698
|
0,015625
|
9
|
48
|
0,001371742
|
0,006712947
|
0,012345679
|
10
|
73
|
0,001
|
0,000949578
|
0,01
|
11
|
75
|
0,000751315
|
0,006375368
|
0,008264463
|
|
|
|
|
|
15
|
153
|
0,000296296
|
0,004656866
|
0,004444444
|
20
|
345
|
0,000125
|
0,00045461
|
0,0025
|
25
|
484
|
0,000064
|
0,002845788
|
0,0016
|
30
|
845
|
3,7037E-05
|
0,000308867
|
0,001111111
|
31
|
783
|
3,35672E-05
|
0,00228595
|
0,001040583
|
32
|
972
|
3,05176E-05
|
0,000277248
|
0,000976563
|
|
|
|
|
|
33
|
900
|
2,78265E-05
|
0,00214597
|
0,000918274
|
В данном случае заданная точность не достигается при n≥33.
Вывод: Получено экспериментальное подтверждение зависимости метода Якоби от вектора начального приближения. Таким образом, мы смогли достичь заданной точности при n до 33.
Эксперимент 2
Зафиксируем значение n = 30 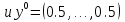 . Будем изменять порядок eps. . Будем изменять порядок eps.
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
30
|
275
|
0,001111111
|
0,071470535
|
0,001111111
|
30
|
845
|
3,7037E-05
|
0,000308867
|
0,001111111
|
30
|
1413
|
1,23457E-06
|
0,002486984
|
0,001111111
|
30
|
1981
|
4,11523E-08
|
0,002565232
|
0,001111111
|
Мы видим, что при значении eps=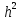 и n=30 заданная точность уже не достигается. Исследуем более подробно случай, когда eps= и n=30 заданная точность уже не достигается. Исследуем более подробно случай, когда eps=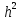 . .
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
5
|
5
|
0,04
|
0,099535082
|
0,04
|
10
|
31
|
0,01
|
0,064396689
|
0,01
|
11
|
22
|
0,008264463
|
0,134577096
|
0,008264463
|
Мы видим, что при eps=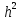 n целесообразно брать до 10 включительно. Далее при увеличении n заданная точность уже не достигается. n целесообразно брать до 10 включительно. Далее при увеличении n заданная точность уже не достигается.
Эксперимент 3
Рассмотрим, как зависит количество шагов итерации, погрешность от уменьшения порядка eps.
Будем менять n при значении 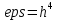 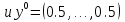
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
10
|
92
|
0,0001
|
0,009117493
|
0,01
|
15
|
239
|
1,97531E-05
|
0,005883609
|
0,004444444
|
20
|
470
|
0,00000625
|
0,004282809
|
0,0025
|
25
|
786
|
0,00000256
|
0,003367734
|
0,0016
|
30
|
1193
|
1,23E-06
|
0,002771514
|
0,001111111
|
Будем менять n при значении 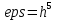 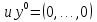
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
10
|
134
|
0,00001
|
0,007646425
|
0,01
|
15
|
353
|
1,31687E-06
|
0,005121005
|
0,004444444
|
20
|
692
|
3,125E-07
|
0,003853261
|
0,0025
|
25
|
1159
|
1,02E-07
|
0,003087237
|
0,0016
|
30
|
1761
|
4,11523E-08
|
0,002574763
|
0,001111111
|
Вывод: При достаточно больших n и eps=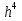 и и 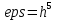 точность достигается. (Если точность достигается при eps= точность достигается. (Если точность достигается при eps=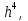 то при то при 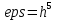 тем более точность достигается при тех же n) тем более точность достигается при тех же n)
Эксперимент 4.
Рассмотрим, как зависит метод от начального приближения.
Пусть начальный вектор  =(0,0, …,0) и eps= =(0,0, …,0) и eps=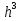 . Тогда: . Тогда:
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
10
|
91
|
0,0001
|
0,009166465
|
0,01
|
15
|
239
|
1,98E-05
|
0,00586313
|
0,004444444
|
20
|
469
|
0,00000625
|
0,004277529
|
0,0025
|
25
|
783
|
0,00000256
|
0,00336791
|
0,0016
|
30
|
1192
|
1,23E-06
|
0,002767627
|
0,001111111
|
Теперь возьмем вектор  =(0.05 ,…, 0.05). =(0.05 ,…, 0.05).
n
|
кол-во итераций
|
eps
|
погрешность
|
h*h
|
10
|
90
|
0,0001
|
0,009003361
|
0,01
|
15
|
238
|
1,97531E-05
|
0,005841149
|
0,004444444
|
20
|
468
|
0,00000625
|
0,004275496
|
0,0025
|
25
|
784
|
0,00000256
|
0,003364847
|
0,0016
|
30
|
1192
|
1,23E-06
|
0,002768912
|
0,001111111
|
По сравнению с предыдущими результатами, при  =(0.05 ,…, 0.05) особых изменений не происходит. Количество итераций меняется от -1 до 1 при n от 10 до 30. =(0.05 ,…, 0.05) особых изменений не происходит. Количество итераций меняется от -1 до 1 при n от 10 до 30.
Теперь возьмем вектор  = (0.1 ,…, 0.1). = (0.1 ,…, 0.1).
N
|
итер
|
eps
|
погрешность
|
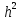
|
5
|
8
|
0.008
|
0.013
|
0.04
|
10
|
58
|
0.001
|
0,0026
|
0.01
|
15
|
119
|
0.00029
|
0.00029
|
0.0044
|
|
 Скачать 151.49 Kb.
Скачать 151.49 Kb.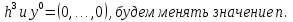
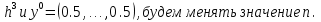
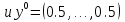 . Будем изменять порядок eps.
. Будем изменять порядок eps.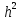 и n=30 заданная точность уже не достигается. Исследуем более подробно случай, когда eps=
и n=30 заданная точность уже не достигается. Исследуем более подробно случай, когда eps=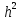 .
. 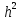 n целесообразно брать до 10 включительно. Далее при увеличении n заданная точность уже не достигается.
n целесообразно брать до 10 включительно. Далее при увеличении n заданная точность уже не достигается. 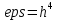
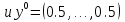
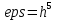
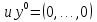
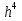 и
и 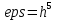 точность достигается. (Если точность достигается при eps=
точность достигается. (Если точность достигается при eps=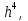 то при
то при 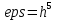 тем более точность достигается при тех же n)
тем более точность достигается при тех же n) =(0,0, …,0) и eps=
=(0,0, …,0) и eps=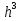 . Тогда:
. Тогда: =(0.05 ,…, 0.05).
=(0.05 ,…, 0.05). =(0.05 ,…, 0.05) особых изменений не происходит. Количество итераций меняется от -1 до 1 при n от 10 до 30.
=(0.05 ,…, 0.05) особых изменений не происходит. Количество итераций меняется от -1 до 1 при n от 10 до 30. = (0.1 ,…, 0.1).
= (0.1 ,…, 0.1).