Методы решения систем линейных алгебраических уравнений
 Скачать 151.49 Kb. Скачать 151.49 Kb.
|
Экспериментальная часть для метода верхней релаксации.Метод релаксации отличается от предыдущих методов собственно наличием релаксационного параметра. Этот параметр лежит на интервале (1;2) и считается оптимальным, когда затрачивается минимальное количество итераций. Покажем, как изменяется количество итераций для n=15, eps= 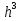 , ,  =(0; 0;…0) и различных значениях �� и найдем оптимальный релаксационный параметр. =(0; 0;…0) и различных значениях �� и найдем оптимальный релаксационный параметр.
Видно, что количество итераций после ��=1.1 колеблется в пределах от 1 до 3. И поэтому сделать конкретный выбор по наиболее оптимальному весу не представляется возможным. Эксперимент 1. Рассмотрим наиболее оптимальные значения w для различных n. Зафиксируем порядок eps = 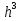 . w будем менять в интервале (1;2). . w будем менять в интервале (1;2).
Мы видим, что точность достигается при достаточно больших n. Эксперимент 2. Зафиксируем значение n=30 и будем менять порядок eps.
Мы видим, что при h заданная точность не достигается. Следовательно, нужно брать eps< 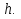 Рассмотрим более подробно случай, когда eps= 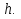
Из таблицы видно, что точность не достигается уже для 12. Это связано с тем, что количество итераций при решении такой СЛУ данным методом недостаточно, чтобы достичь точность о(h). Поэтому мы можем сделать вывод, что использовать для данной СЛУ в условии остановки метода eps= 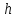 нецелесообразно. нецелесообразно.Эксперимент 3. Проведем эксперимент с разными начальными векторами  . Зафиксируем eps= . Зафиксируем eps=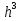 . . =(0,0, …,0) =(0,0, …,0)
 = (0.1 ,…, 0.1) = (0.1 ,…, 0.1)
 =(b[1]/A[1][1], …, b[n]/A[n][n]) =(b[1]/A[1][1], …, b[n]/A[n][n])
Вывод: Из таблиц мы видим, что начальное приближение влияет на погрешность. В данном случае в качестве начального приближения целесообразнее брать  =(0,0, …,0), так как в других случаях погрешность выше. =(0,0, …,0), так как в других случаях погрешность выше. |
