да. Высшая математика. Методические рекомендации для их выполнения по дисциплине Высшая математика
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Раздел 5 [1]: глава 8, §§ 1- 4. [2]: глава 15, §§ 1-12. [3]: глава 15, §§ 1-6 . Вопросы для самопроверки Дайте определение непрерывной функции нескольких (например, двух) переменных. Дайте определение частных производных и полного дифференциала. Как они связаны? Что называется градиентом функции нескольких переменных? Дайте определение экстремума функции нескольких переменных и приведите необходимые условия экстремума. Как определяются частные производные? После изучения этих тем можно приступать к выполнению четвертой задачи контрольной работы. Задача 4 Найти z//yx; z//yy; z//xy; z//xx функции z= 3х + х2 у3 . Написать уравнение линий уровня f (x; y) = c при c= 0 и с = 1. Найти gradz в точке М0 (-1; 1). Решение: Учитывая формулы (15.1) и (15.2) § 3 главы 15 [2] и обычные правила дифференцирования функции одной переменной, находим частные производные первого порядка. При этом следует помнить, что при вычислении частной производной по х , мы считаем у постоянной. Аналогично, при нахождении частной производной по у считаем х постоянной. ∂ z ∂ z   /x = = (3x + x2 y2) = 3 + 2xy3 /x = = (3x + x2 y2) = 3 + 2xy3 ∂ x ∂ x ∂ z ∂ z   /y = = (3x + x2 y2) = 0 + 3x2 y2 = 3x2 y2 /y = = (3x + x2 y2) = 0 + 3x2 y2 = 3x2 y2 ∂ y ∂ y Теперь найдем частные производные второго порядка: ∂2 z ∂ z   //xx = (z/x)/x = = (3 + 2xy6 ) = 0 + 2y3 = 2y3 //xx = (z/x)/x = = (3 + 2xy6 ) = 0 + 2y3 = 2y3 ∂ x2 ∂ x ∂2 z ∂ z   //yy = (z/y)/y = = (3x2 y2 ) = 6x2 y //yy = (z/y)/y = = (3x2 y2 ) = 6x2 y∂ y2 ∂ y ∂ z  //xy = (z/x)/y = (3 + 2xy3 ) = 0 + 6xy2 = 6xy2 //xy = (z/x)/y = (3 + 2xy3 ) = 0 + 6xy2 = 6xy2 ∂ y ∂ z  //yx = (z/y)/x = (3x2 y2 ) = 3y2 ∙ 2x = 6xy2 //yx = (z/y)/x = (3x2 y2 ) = 3y2 ∙ 2x = 6xy2 ∂ x Запишем уравнения линий уровня. Как известно, линии уровня образуют на плоскости семейство параллельных кривых, на каждой из которых функция принимает постоянное значение f (x; y) = с. При с = 0 имеем линию нулевого уровня: 3х + х2 у3 = 0. При с = 1 уравнение линии уровня: 3х + х2 у3 = 1 При переходе от одной линии уровня к другой значение функции изменяется.  ∂ z ∂ z ∂ z ∂ zН   аправление возрастания функции указывает вектор gradz = ; аправление возрастания функции указывает вектор gradz = ;∂ x ∂ y Найдем направление градиента в точке М0 (-1; 1). Имеем ∂   z ∂ z z ∂ z  M0 = 3 + 2 ∙ (-1) ∙ (1)3 = 1; M0 = 3 ∙ (-1)2 ∙ 12 = 3. M0 = 3 + 2 ∙ (-1) ∙ (1)3 = 1; M0 = 3 ∙ (-1)2 ∙ 12 = 3.∂ x ∂ x Поэтому gradz = {1; 3} в точке М0. Раздел 6 [1]: глава 4, § 1-5 (часть 2). [2]: глава 12, § 1-9. [3]: глава 12, § 1-7. Вопросы для самопроверки Дайте определение дифференциального уравнения и основных понятий, связанных с ним (порядок решения, общее решение, частное решение и интегральная кривая). Как можно геометрически истолковать общее и частное решение? Изложите методы решения основных типов дифференциальных уравнений первого порядка (с разделяющимися переменными, однородных и линейных). Изложите методы решения основных типов дифференциальных уравнений второго порядка (с понижением порядка, однородных и линейных). После разбора этих тем можно приступить к выполнению пятой задачи контрольной работы. Задача 5 Найдите решение дифференциального уравнения у// + 4у/ + 3у = е –2х, удовлетворяющее начальным условиям у (0) = 2, у/ (0) = 0. Решение В соответствии с теоремой 3 §8 главы 12 книги [2] общее решение данного неоднородного линейного уравнения есть сумма его частного решения и общего решения соответствующего ему линейного однородного дифференциального уравнения у// + 4у/ + 3у = 0. Ищем общее решение однородного уравнения. В соответствии с формулами 12.38 из § 8 главы 12 книги [2] это решение записывается в виде у 0 = С1 ек1х + С ек2х , где С1 и С2 – произвольные постоянные, а k1 и k2 – корни характеристического уравнения ak2 + bk+ c = 0 данного уравнения ay// + by/ + cy = 0. В нашем случае а = 1, b = 4, c = 3. Характеристическое уравнение принимает вид: k2 + 4k + 3 = 0, его корни k1 = -3, k2 = -1, значит, общее решение однородного уравнения имеет вид: у0 = С1 е-3х + С2 е-х. Найдем частное решение неоднородного уравнения. Поскольку правая часть данного уравнения содержит в показателе степени коэффициент (-2), не являющийся корнем характеристического уравнения, частное решение следует искать в виде: у1 = de –2x . Найдем неизвестный коэффициент d. Так как у/1 = 2de –2x, у//1 = -4 de –2x , подставив значения у1, у/1, у//1 в данное уравнение, получим равенство 4de –2x – 8de–2x + 3de –2x = e –2x откуда – de –2x = e –2x, т.е. d = -1. Таким образом, общее решение данного дифференциального уравнения имеет вид у = у0 + у1 = С1 е –3х + С2 е –х – е –2х Найдем то решение, которое удовлетворяет данным начальным условиям. Так как у/ = -3 С1 е –3х + С2 е –х – 2е –2х, у (0) = С1 + С2 – 1, у/ (0) = -3 С1 – С2 + 2, то решая систему уравнений: С1 + С2 – 1 = 2, -3 С1 – С2 = 0, находим С1 = -0,5; С2 = 3,5. Следовательно, у = -0,5 –3х + 3,5е –х – е –2х - искомое решение. Ответ: у = -0,5 –3х + 3,5е –х – е –2х Задачи 01-20 Найти предел: 01. а) б) 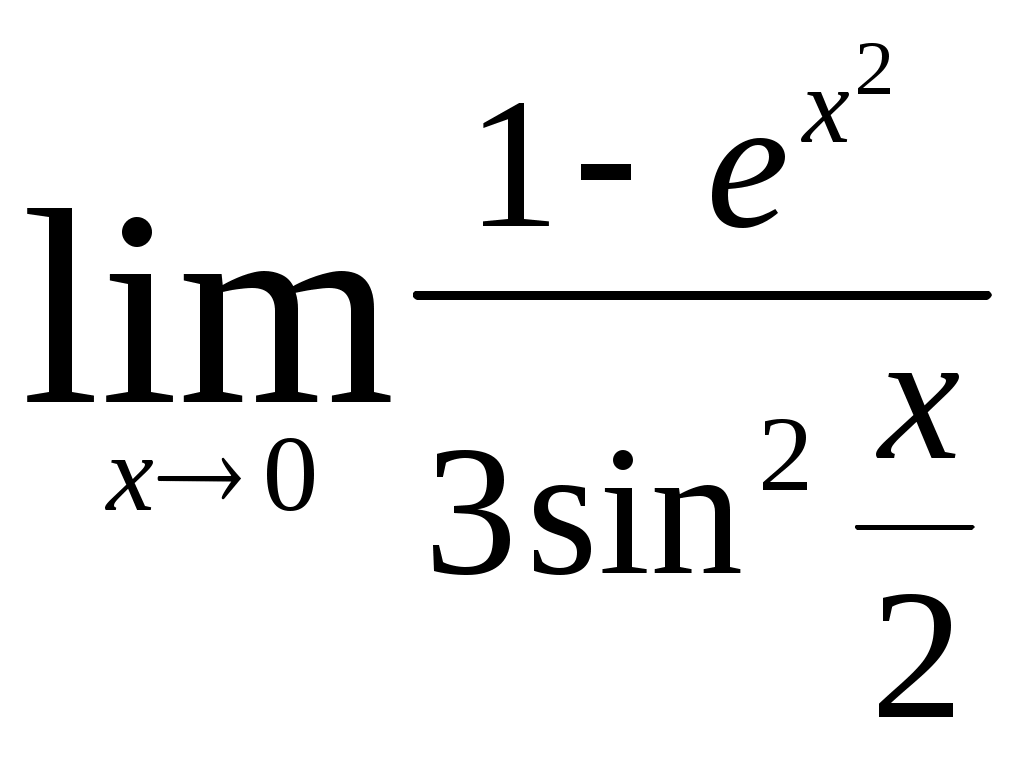 02. а) 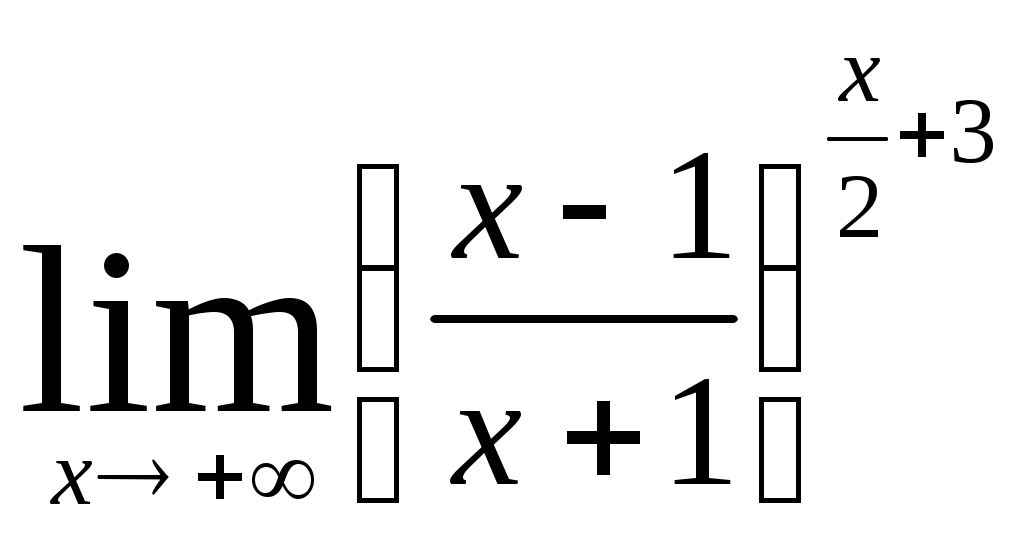 б) 03. а) б) 04. а) б) 05. а) 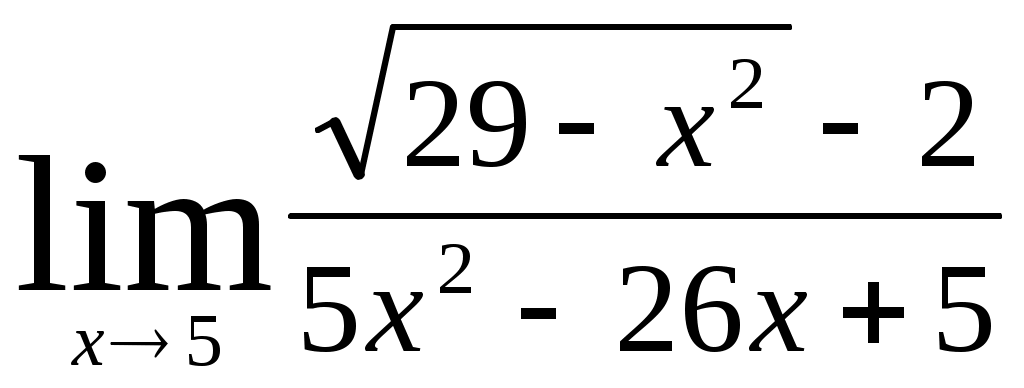 в) в) б) 06. а) б) 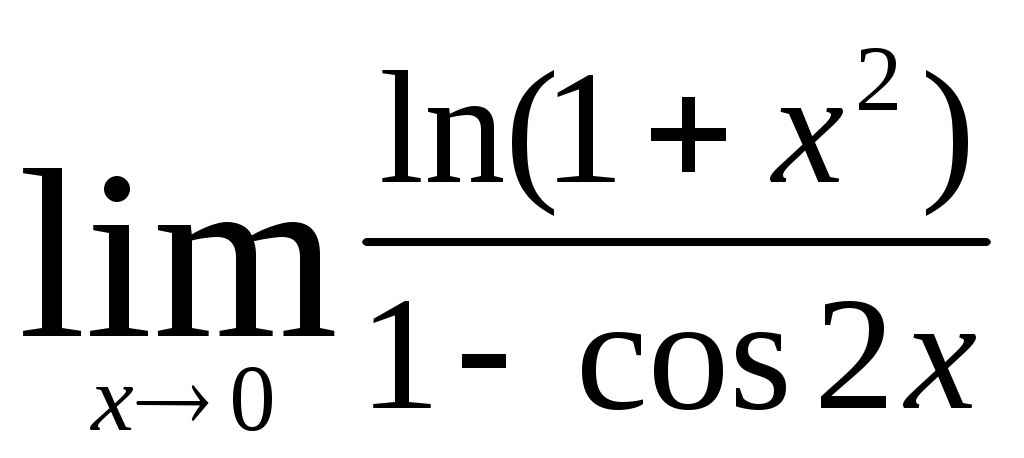 07. а) б) 08. а) б) 09. а) б) 10. а)  в) в) б) 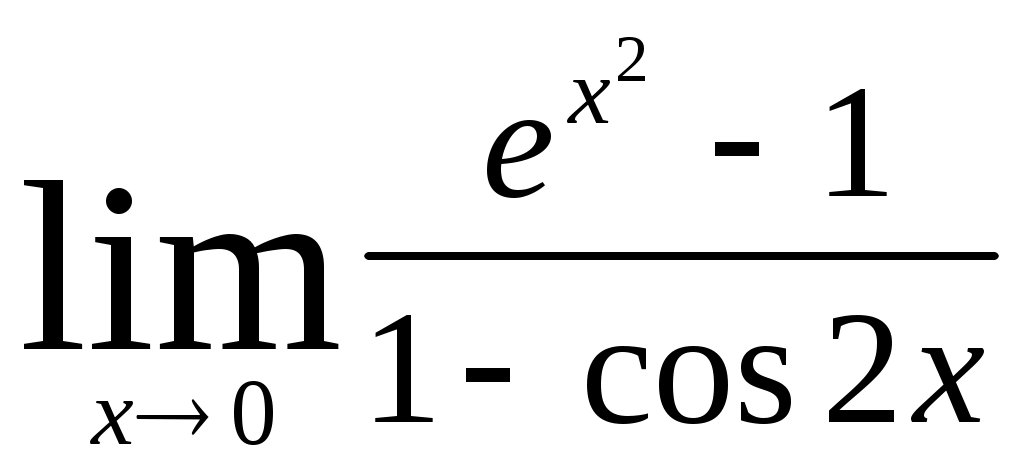 11. а) б) 12. а) б) 13. а) б) 14. а) б) 15. а) 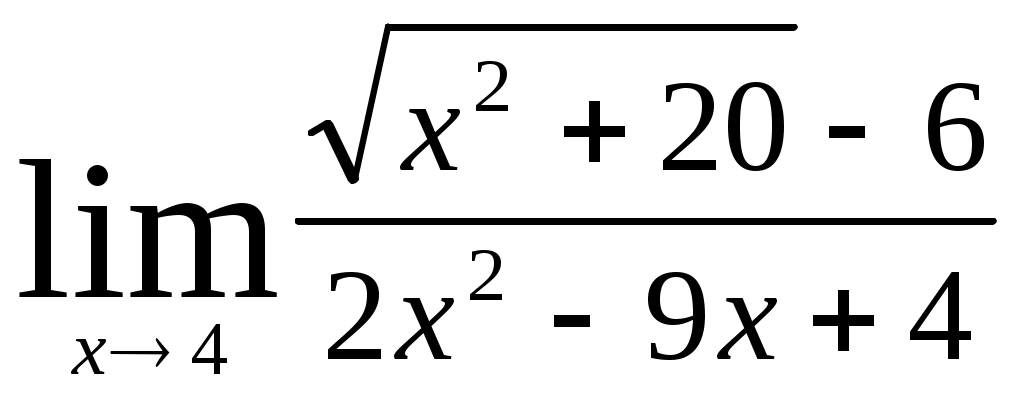 в) в) б) 16. а) б) 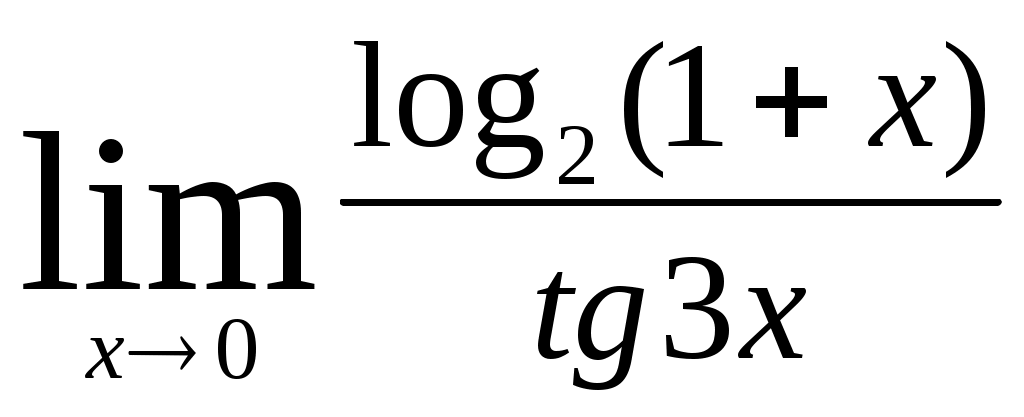 17. а) б) 18. а) б) 19. а) б) 20. а) б) 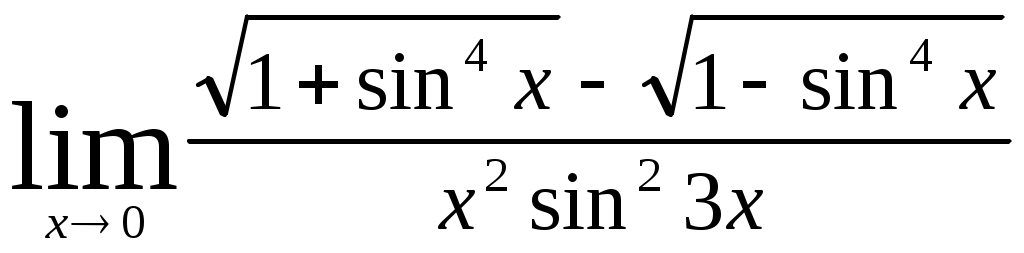 г) г) Задачи 21-40 Исследовать функцию у = f (x) и построить ее график: 21. 23. 25. 27. 29. 31. 33. 35. 37. 39. Задачи 41-60 Вычислить площадь фигуры, ограниченной линиями у = ах2 + bx и у = сх2 + dx
Задачи 61-80 Найти z//xx ; z//yy ; z//xy ; z//yx функции z = f (x; y). Написать уравнение линии уровня f (x; y) = С при С = 0 и С = 1. Найти gradz в точке М0. 61. z = ½ x2y – 2y2; M0 (0; -2); 62. z = -xy3 + 3x2; M0 (2; 1); 63. z = 3xy – x2y3; M0 (1; 1); 64. z = 5x2y3 – 3y2; M0 (-1; 1); 65. z = -3xy4 + x2y; M0 (2; 0); 66. z = xy2 + 3/2 x2y4; M0 (-2; 1); 67. z = - 1/3 x3 + 2xy3; M0 (2; -1); 68. z = 2/3 x3y6 – 2xy; M0 (1; -1); 69. z = 3x2y – 2xy2; M0 (2; 1); 70. z = -2xy + 4x3y3; M0 (1; 1); 71. z = ½ x2 + ¼ xy4; M0 (1; 0); 72. z = 1/3 y3 – ½ x2y2; M0 (2; 1); 73. z = 3x2y – ¼ x4; M0 (1; 2); 74. z = -x2y + 1/3 y3; M0 (1; -2); 75. z = -1/3 x3 + xy; M0 (0; 2); 76. z = xy + 5x2y; M0 (1; 0); 77. z = ½ y2 – x2y; M0 (-1; 3); 78. z = xy – ½ x2y2; M0 (2; 1); 79. z = x2y – xy2; M0 (0; -1); 80. z = 2y3 + 3x2; M0 (2; -1). Задачи 81-100 Найдите решение дифференциального уравнения ау// + by/ + cy = ekx , удовлетворяющее начальным условиям: у (0) = р, у/ (0) = g.
Вопросы для зачета Что называется функцией? Каковы способы ее задания? Что называется областью определения функции? Что называется графиком функции? Дайте определение конечного предела функции в точке. Дайте определения конечного предела функции при x →+∞ и при х→-∞. Как связаны понятия: «предел функции в точке» и «пределы функции в точке слева и справа»? Что такое бесконечно малая величина? Сформулируйте основные теоремы о бесконечно малых величинах. Что такое бесконечно большая величина и как она связана с бесконечно малой? Сформулируйте основные теоремы о пределах. Напишите первый и второй замечательные пределы. Какие теоремы о пределах используются при их вычислении? Дайте определения функции, непрерывной в точке и на отрезке. Сформулируйте основные теоремы о непрерывных функциях. Какие типы точек разрыва функции Вы знаете? Приведите примеры. Что называется производной функции? Найдите производную функции у = х3, пользуясь только определением производной. Что называется касательной к кривой в данной точке? Каков геометрический смысл производной? Как составить уравнение касательной? Каков механический смысл производной? Может ли функция иметь производную в точке разрыва? Будет ли функция непрерывна в точке, если она в ней дифференцируема? Перечислите правила дифференцирования и формулы дифференцирования основных элементарных функций. Производная сложной функции. Что называется дифференциалом функции? Его основные свойства. Каков геометрический смысл дифференциала функции в точке при заданном приращении аргумента? Какие свойства дифференциала функции Вы знаете? Сформулируйте теоремы Ролля и Лангранжа. Дайте определение возрастания (убывания) функции. В чем состоит необходимый и достаточный признак возрастания (убывания) функции? Дайте определение максимума (минимума) функции. В чем состоит необходимый признак экстремума? Какая функция называется первообразной данной функции? Что называется неопределенным интегралом от данной функции? Запишите таблицу простейших интегралов. Как производится замена переменной в неопределенном интеграле? Как производится интегрирование по частям в неопределенном интеграле? Назовите основные свойства неопределенного интеграла. Что называется определенным интегралом от данной функции? Каков его геометрический смысл? Как связаны между собой понятия определенного и неопределенного интеграла? Сформулируйте теорему о производной определенного интеграла с переменным верхним пределом. Перечислите основные свойства определенного интеграла. Дайте определение несобственных интегралов с бесконечным пределом интегрирования. Дайте определение непрерывной функции нескольких (например, двух) переменных. Дайте определение частных производных и полного дифференциала. Как они связаны? Что называется градиентом функции нескольких переменных? Дайте определение экстремума функции нескольких переменных и приведите необходимые условия экстремума. Как определяются частные производные? Дайте определение дифференциального уравнения и основных понятий, связанных с ним (порядок решения, общее решение, частное решение и интегральная кривая). Как можно геометрически истолковать общее и частное решение? Изложите методы решения основных типов дифференциальных уравнений первого порядка (с разделяющимися переменными, однородных и линейных). Изложите методы решения основных типов дифференциальных уравнений второго порядка (с понижением порядка, однородных и линейных). |
