Э_1_Эконометр._Магистр.. — копия. Методические рекомендации для выполнения задания стр. 3 Задание Изучение специальных методов построения регрессионных моделей
 Скачать 285.41 Kb. Скачать 285.41 Kb.
|
Временные ряды: модели тренда и сезонности.1. Этапы построения модели тренда и сезонности.Анализ временных рядов (time series analysis) базируется на идее: результирующая переменная складывается под влиянием очень большого числа факторов, многие из которых не поддаются идентификации и непосредственному наблюдению и измерению. Поэтому лучшим источником информации о совокупности влияния всех этих факторов являются значения самой исследуемой переменной в прошлые моменты времени и значения ошибок. Простейшим подходом к моделированию временных рядов, содержащих сезонные колебания, является построение аддитивной или мультипликативной моделей временного ряда. Выбор одной из этих моделей основывается на анализе структуры временного ряда. Если амплитуда сезонных колебаний примерно постоянна, то строят аддитивную модель. Если же амплитуда колебаний непостоянна, то есть возрастает или уменьшается, то строят мультипликативную модель. Процесс построения модели ряда в этом случае включает следующие этапы: Выравнивание исходного ряда методом скользящей средней. Расчет значений сезонной компоненты S. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных 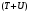 в аддитивной или в аддитивной или 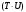 в мультипликативной модели. в мультипликативной модели.Аналитическое выравнивание уровней 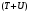 или или 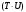 и расчет значений T с использованием полученного уравнения тренда. и расчет значений T с использованием полученного уравнения тренда.Расчет полученных по модели значений 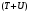 или или 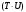 . .Расчет абсолютных и/или относительных ошибок. Аддитивная модель Рассмотрим процесс построения аддитивной модели на примере. Дан объем продаж предприятия (тыс. руб.) за 11 кварталов (табл. 11). На основании данных составить прогноз на последующие 2 квартала с использованием аддитивной и мультипликативной моделей. Для аддитивной модели фактическое значение A=T (тренд, полученный по модели) +S (сезонная вариация) +U (ошибка). На первом шаге нужно исключить влияние сезонной вариации. Для этого используется метод скользящей средней (табл. 11, 12). Таблица 11
Расчет оценки сезонной вариации Таблица 12
Оценки сезонной вариации запишем под соответствующим номером квартала в году. Результат запишем в строке «Среднее». Сумма = –1. Скорректируем значения в строке «Среднее», чтобы общая сумма была равна 0. Это необходимо для усреднения значения сезонной вариации в целом за год. Корректирующий фактор вычисляется следующим образом: сумма оценок сезонных вариаций (– 1) делится на число кварталов в году (4). Поэтому из каждого числа этой строки нужно вычесть величину, равную – 1/4 = –0,25 (один из вариантов из нечетного столбца вычесть – 0,3 , из четного –0,2). В последней строке получены значения сезонной вариации за год (табл. 13). Исключить сезонную вариацию из фактических данных. Пусть уравнение линии тренда 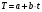 . . Расчет скорректированной сезонной вариации Таблица 13
После стандартных вычислений (тема «Парная регрессия») имеем 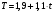 . .Расчет трендового значения для аддитивной модели Таблица 14
Необходимо дать прогноз продаж на последующие два квартала. Для расчета прогноза поставить номера кварталов в формулу и учесть сезонную вариацию: (1,9 + 1,1∙12) + (–0,9) = 14,2 (4 квартал), (1,9 + 1,1∙13) + 2 = 18,2 (1 квартал). Далее рассчитаем абсолютную ошибку. Качество полученной модели можно проверить, используя сумму квадратов абсолютных ошибок. Сумма квадратов абсолютных ошибок равна 16,58. По отношению к сумме квадратов отклонений исходных уровней ряда от его среднего уровня, равной 148,72, эта величина составит 11 %. Следовательно, аддитивная модель объясняет 89 % общей вариации объема продаж. Мультипликативная модель В некоторых временных рядах значение сезонной вариации – это определенная доля трендового значения, сезонная вариация увеличивается с возрастанием значений тренда. В этих случаях используется мультипликативная модель: A=T∙S∙U. Дан объем продаж (тыс. руб.) за 11 кварталов. На основании данных составить прогноз на последующие 2 квартала. Исходные данные для решения задачи Таблица 15
На первом шаге нужно исключить влияние сезонной вариации. Для этого используется метод скользящей средней. Значения сезонной вариации – это доли, где число сезонов равно 4. Поэтому необходимо, чтобы сумма средних была равна 4, а в примере 3.994. Следовательно, итоговые коэффициенты сезонности нужно умножить на множитель 4/3.994. это последняя строка – скорректированная сезонная вариация. Как показывают полученные оценки, в 1-ом, 2-ом, 3-ем кварталах объём продаж снижается соответственно на 23.3 %, 11.9 %, 4.8 % от соответствующих трендовых значений. Уравнение линии тренда T=a+b∙t. Найти коэффициенты a,b по стандартной методике, описанной в теме «Парная регрессия». В результате 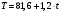 , где t– номер квартала. Для прогноза подставить номер квартала в формулу и учесть сезонную вариацию. , где t– номер квартала. Для прогноза подставить номер квартала в формулу и учесть сезонную вариацию.Прогноз на 12 квартал: (81,6 + 1,2∙12)∙1,41=135,4 (тыс. руб.). Прогноз на 13 квартал: (81,6+1,2∙13)∙0,757 = 73,6 (тыс. руб.). Затем необходимо рассчитать ошибки. Расчет оценки сезонной вариации, трендового значения для мультипликативной модели Таблица 16
Расчет коэффициента сезонности Таблица 17
Среднеквадратическая ошибка 17,1/11 = 1,6. Поскольку ошибки составляют порядка 1 %, то можно говорить о хороших краткосрочных прогнозах. Качество полученной модели можно проверить, используя сумму квадратов абсолютных ошибок. Общая сумма квадратов абсолютных ошибок равна 17,1. По отношению к сумме квадратов отклонений исходных уровней ряда от его среднего уровня, равной 4546,7, эта величина составит 0,397 %: (17.1/4546.7)∙100 = 3.97 %. Следовательно, мультипликативная модель объясняет 96.03 % общей вариации продаж. Выбрать из таблицы наблюдений произвольный вариант заданий и построить 2-е модели временных рядов: аддитивную и мультипликативную, следуя примеру. Разработать одномерную аддитивную модель временного ряда и сделать прогноз на три квартала вперёд, предварительно построив автокорреляционную функцию ряда для анализа его структуры.
Разработать одномерную мультипликативную модель временного ряда и сделать прогноз на три квартала вперёд, предварительно построив автокорреляционную функцию ряда для анализа его структуры.
Задание 4. Модели одновременных уравнений 4.1. Цель и содержание задания Цель задания: изучение систем взаимозависимых эконометрических моделей Содержание задания: имеются следующие экономические показатели национальной экономики, представленные в таблице:
Определите параметры структурной модели следующего вида: 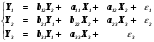 Задание 2. Имеется следующая гипотетическая структурная модель: 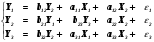 Приведённая форма исходной модели имеет вид 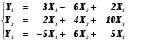 Проверить структурную форму модели на идентификацию. Определить структурные коэффициенты модели. 4.2 Методические рекомендации для выполнения задания Для решения поставленных задач необходимо воспользоваться примером, расположенным ниже по тексту(косвенный метод МНК). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
