Э_1_Эконометр._Магистр.. — копия. Методические рекомендации для выполнения задания стр. 3 Задание Изучение специальных методов построения регрессионных моделей
 Скачать 285.41 Kb.
|
Динамические эконометрические моделиОбщая характеристика моделей с распределенным лагом и моделей авторегрессии.Во многих экономических задачах встречаются лагированнные (взятые в предыдущий момент времени) переменные. Например, yt- выпуск предприятия за год t - может зависеть не только от инвестиций It в этот год, но и от инвестиций в предыдущие годы. Эконометрическая модель, содержащая в качестве факторов не только текущие переменные, но и лаговые их значения, называется динамической. Выделим два основных типа динамических эконометрических моделей: модели с распределенным лагом; модели авторегрессии. Моделями с распределенным лагом называются модели, содержащие в качестве факторов лаговые значения факторных переменных. Например, модель вида  .Моделями авторегрессии называются модели, содержащие в качестве факторов лаговые значения зависимой переменной. Например, модель вида .Обе модели включают в себя лаговые значения переменных, но существенно различаются с точки зрения статистического оценивания параметров. Модели с распределенным лагом Модель с распределенным лагом в предположении, что максимальная величина лага конечна, имеет вид:  .В этой модели влияние x на y сохраняется в течение времени p. В краткосрочном (текущем) периоде влияние x на y отражается величиной β0, называемой краткосрочным мультипликатором. В долгосрочном периоде (через p моментов времени) суммарное влияние x на y отражается величиной 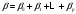 , называемой долгосрочным мультипликатором.В моделях с распределенным лагом объясняющие переменные некоррелированы со случайным членом, поэтому модель можно оценивать с помощью обычного МНК. Однако на практике оценка параметров модели затруднительна из-за высокой мультиколлинеарности факторов. Для уменьшения числа объясняющих переменных и уменьшения эффекта мультиколлинеарности разработан ряд подходов, например, модель геометрических лагов и модель полиномиальных лагов. Модель геометрических лагов Предположим, что в модели с бесконечным лагом коэффициенты при лаговых значениях объясняющих переменных убывают в геометрической прогрессии. Модель имеет вид
В этой модели влияние x на y продолжается бесконечно. В краткосрочном (текущем) периоде влияние x на y отражается коэффициентом β0. В долгосрочном периоде суммарное влияние x на y равно  .Модель содержит только три параметра (α, β0, δ) и является нелинейной. Процедура оценивания нелинейной модели заключается в следующем: перебирается с некоторым шагом значение δ из интервала (0;1); для каждого δ рассчитывается 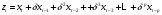 с таким значением p, при котором дальнейшие лаговые значения x не оказывают существенного воздействия на z; оценивается уравнение регрессии 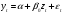 ;выбирается такое значение δ, которое обеспечивает наибольший коэффициент детерминации R2 при оценке уравнения. Выбранному δ соответствуют вычисленные значения α, β0 этого уравнения. Использование этого метода при оценке параметров позволяет избежать проблему мультиколлинеарности объясняющих переменных. Модель полиномиальных лагов (метод Алмон) В модели полиномиальных лагов предполагается, что зависимость коэффициентов при лаговых значениях объясняющей переменной от величины лага описывается полиномом m-й степени. Модель имеет вид ,где 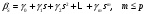 .Предположим, что величина лага p известна. Кроме того, необходимо установить степень полинома m. Обычно на практике ограничиваются рассмотрением полиномов второй и третьей степени. Пусть, например, p=3 m=2, тогда исходная модель есть  ,
Преобразованная модель имеет вид  ,
Используя МНК, оцениваем параметры преобразованной модели и затем рассчитываем параметры исходной модели с распределенным лагом. Пример. Имеются данные об объеме валового внутреннего продукта у некоторой страны в зависимости от инвестиций x в ее экономику за 25 лет. Построим модель с распределенным лагом для p=3 в предположении, что структура лага описывается полиномом второй степени. Общий вид исходной модели: .Исходные данные (yt,xt) и преобразованные (z0,z1,z2) данные (усл. ед.) представлены в следующей таблице:
Оцененная исходная модель имеет вид  ,в которой коэффициент 0,71 при переменной xt-1 незначим (в скобках указаны стандартные ошибки). Оцененная преобразованная модель имеет вид   ,и все коэффициенты при переменных значимы. Получили следующие оценки параметров преобразованной модели:  .Коэффициенты регрессии исходной модели:  Таким образом, модель с распределенным лагом имеет вид  .Краткосрочный мультипликатор равен 2,32, а долгосрочный мультипликатор равен 2,32+0,96+0,72+1,6=5,6. Это означает, что увеличение инвестиций в экономику страны на 1 усл. ед. приведет к росту валового внутреннего продукта в среднем на 2,32 усл. ед. в текущем периоде и на 5,6 усл. ед. через 3 года. Учебная литература, ресурсы информационно-коммуникационной сети Интернет и иные источники, рекомендуемые для выполнения заданий Кремер Н.Ш., Путко Б.А. Эконометрика, ЮНИТИ, 2008, 311с. Меняйлов А.И., М Волков Г.А., Меняйлова М.А.. М. Эконометрика: учебно-методическое пособие. - Красногорск: ООО «Красногорская типорафия», 2013.-92 с. Носков В.П. Эконометрика. Кн.1.Ч1,2: учебник – М.: Издательский дом «Дело» РАНХиГС, 2011.- 672 с.(Сер. «Академический учебник».) Носков В.П. Эконометрика. Кн.2.Ч3,4: учебник – М.: Издательский дом «Дело» РАНХиГС, 2011.- 576 с.(Сер. «Академический учебник».) Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2008 Эконометрика: Учебник /Под ред. Елисеевой И.И. – М.: Финансы и статистика, 2009.- 288с http://www.nsu.ru/ef/tsy/ecmr/study.htm http://www.nsu.ru/ef/tsy/ecmr/index.htm |
,
.
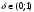