Э_1_Эконометр._Магистр.. — копия. Методические рекомендации для выполнения задания стр. 3 Задание Изучение специальных методов построения регрессионных моделей
 Скачать 285.41 Kb. Скачать 285.41 Kb.
|
Проверка регрессионной модели на автокорреляцию остатковРегрессионные модели в экономике часто содержат стохастические зависимости между значениями случайных ошибок – автокорреляцию ошибок. Ее причинами являются: во-первых, влияние некоторых случайных факторов или опущенных в уравнении регрессии важных объясняющих переменных, которое не является однократным, а действует в разные периоды времени; во-вторых, случайный член может содержать составляющую, учитывающую ошибку измерения объясняющей переменной. Применение к модели с автокорреляцией остатков обыкновенного МНК приведет к следующим последствиям: Выборочные дисперсии полученных оценок коэффициентов будут больше по сравнению с дисперсиями по альтернативным методам оценивания, т. е. оценки коэффициентов будут неэффективны. Стандартные ошибки коэффициентов будут оценены неправильно, чаще всего занижены, иногда настолько, что нет возможности воспользоваться для проверки гипотез соответствующими точными критериями – мы будем чаще отвергать гипотезу о незначимости регрессии, чем это следовало бы делать в действительности. Прогнозы по модели получаются неэффективными. На практике исследователь в этом случае поставлен перед проблемой тестирования наличия в модели автокорреляции, а также выявления причины автокорреляции при ее обнаружении: или в модели опущена существенная переменная, или структура ошибок зависит от времени. То есть исследование остатков позволяет судить о правильности модели и ее пригодности для прогнозирования. Способом проверки существования автокорреляции является применение статистических критериев. Хорошо известен критерий Дарбина – Уотсона, который определяется следующим образом: Если критерий равен двум, то не существует положительной автокорреляции. Если он равен нулю, то существует совершенная положительная автокорреляция, если равен четырем, то имеет место совершенная положительная автокорреляция. Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина–Уотсона. Если DW ≈ 2, мы считаем отклонение от линии регрессии случайными, не связанными друг с другом. Это означает, построенная линейная регрессия, вероятно, отражает реальную зависимость. Скорее всего, не осталось неученых существенных факторов, влияющих на зависимую переменную. Какая-либо другая нелинейная формула не превосходит по статистическим характеристикам предложенную линейную зависимость. В этом случае, даже когда 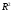 невелико, вполне вероятно, что необъяснённая дисперсия вызвана влиянием на зависимую переменную большого числа различных факторов, индивидуально слабо влияющих на исследуемую переменную, и может быть описана как случайная нормальная ошибка. невелико, вполне вероятно, что необъяснённая дисперсия вызвана влиянием на зависимую переменную большого числа различных факторов, индивидуально слабо влияющих на исследуемую переменную, и может быть описана как случайная нормальная ошибка.Возникает вопрос, какие значения DW можно считать статистически близкими к двум? Для ответа на этот вопрос разработаны специальные таблицы критических точек статистики Дарбина – Уотсона, позволяющие при данном числе наблюдений n, количестве объясняющих переменных k и заданном уровне значимости  определять границы приемлемости (критические точки) наблюдаемой статистики DW. определять границы приемлемости (критические точки) наблюдаемой статистики DW. Для заданных 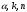 в таблице указываются два числа: в таблице указываются два числа: 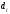 – нижняя граница (индекс – первая буква слова low), и – нижняя граница (индекс – первая буква слова low), и 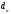 – верхняя граница (индекс – первая буква слова up). Для проверки гипотезы – верхняя граница (индекс – первая буква слова up). Для проверки гипотезы 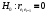 (об отсутствии автокорреляции остатков) используется числовой отрезок, изображённый ниже. (об отсутствии автокорреляции остатков) используется числовой отрезок, изображённый ниже.Пусть n– число наблюдений, m – число факторов модели. Для уровня значимости α=0,05 по таблицам распределения Дарбина – Уотсона (табл. 8) найти числа dl, du. Значения статистик dl, du. для критерия Дарбина – Уотсона при α=0,05 для двух объясняющих переменных Таблица **
DW                0 dl du 2 4-du 4-dl 4 Область Область принятия Область  отклонения H0 гипотезы H0 отклонения H0 Положительная Область Отрицательная автокорреляции неопределённости автокорреляция Выводы осуществляются по следующей схеме. Если DW < dl, то это свидетельствует о положительной автокорреляции остатков. Если DW > 4 – dl, то это свидетельствует об отрицательной автокорреляции остатков. Если dl < DW < du или 4 – du < DW < 4– dlто гипотеза 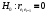 (об отсутствии автокорреляции) не может быть ни принята, ни отклонена. (об отсутствии автокорреляции) не может быть ни принята, ни отклонена.Не обращаясь к таблице критических точек Дарбина-Уотсена, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если 1,5 < DW < 2,5. Для более надёжного вывода целесообразно обращаться к табличным значениям. Тест можно применять только в случае выполнения следующих условий: в уравнении присутствует свободный член, регрессоры являются нестохастическими, в уравнении нет лаговых значений зависимых переменных, регрессионные остатки должны быть в последовательных наблюдениях. Отсутствие автокорреляции подтверждает высокое качество модели. При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным. В результате освоения дисциплины «Эконометрика», продвинутый курс студент должен: Знать: • методы построения эконометрических моделей объектов, явлений и процессов, необходимых для решения финансовых и экономических задач (основные научные принципы и базовые понятия эконометрического моделирования); методы спецификации, параметризации и верификации эконометрических моделей; основные принципы классификации (типологии) эконометрических моделей; методы практического построения и анализа эконометрических моделей. Уметь Строить на основе описания ситуаций стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты; прогнозировать на основе стандартных теоретических и эконометрических моделей поведение экономических агентов, развитие экономических процессов и явлений, на микро- и макроуровне; представлять результаты аналитической и исследовательской работы в виде выступления, доклада, информационного обзора, аналитического отчета, статьи; строить эконометрические модели парной и множественной линейной и нелинейной регрессии и проводить корреляционный анализ; строить эконометрические модели в виде системы эконометрических одновременных уравнений; строить эконометрические модели типа временных рядов, обладать навыками эконометрического оценивания и прогнозирования экономических явлений; использовать современные компьютерные технологии и соответствующие пакеты прикладных программ при разработке многомерных эконометрических моделей. Владеть современной методикой построения эконометрических моделей; методами и приемами анализа экономических явлений и процессов с помощью стандартных теоретических и эконометрических моделей; современными методиками расчета и анализа социально-экономических показателей, характеризующих экономические процессы и явления на микро- и макроуровне; навыками самостоятельной работы, самоорганизации и организации выполнения поручений; Задание 2 2.1. Цель и содержание задания Цель задания: изучение специальных методов построения регрессионных моделей; использование фиктивных переменных в эконометрических моделях Содержание задания: Брокерская фирма исследует вопрос об объёмах продаж акций в зависимости от цены Пусть Хi - средняя цена одной акции в i -ю неделю, Уi -количество проданных акций Ниже приведены данные за 30 недель. Построить эконометрическую модель ценовой политики брокерской фирмы Оценить качество построенной модели с помощью эконометрических критериев Добиться значения критерия детерминации R2 не менее 0,96. 2.2. Методические рекомендации для выполнения задания Рекомендуем ввести дополнительные бинарные переменные для аномальных значений Yi={0,1}
Задача 17. Исследуется надёжность станков трёх производителей A, B, C. При этом учитывается возраст станка М (в месяцах) и среднее время Т (в часах) безаварийной работы до последней поломки. Построить эконометрическую модель надежности (среднего времени безаварийной работы) станочного парка предприятия. Оценить качество построенной модели с помощью эконометрических критериев - индекса детерминации R2 и критериев Стьюдента t и Фишера F. Выборка из 40 станков дала следующие результаты. 
Задание 3. Модели временные ряды: аддитивные и мультипликативные модели тренда и сезонности. 3.1. Цель и содержание задания Цель задания: изучение методов построения моделей временных рядов Содержание задания: разработать одномерную аддитивную модель временного ряда и сделать прогноз на три квартала вперёд, предварительно построив автокорреляционную функцию ряда для анализа его структуры. 3.2. Методические рекомендации для выполнения задания При построении моделей временных рядов следует придерживаться ниже следующих примеров расчётов. |

 Фирма
Фирма T
T