Э_1_Эконометр._Магистр.. — копия. Методические рекомендации для выполнения задания стр. 3 Задание Изучение специальных методов построения регрессионных моделей

• Название: Методические рекомендации для выполнения задания стр. 3 Задание Изучение специальных методов построения регрессионных моделей
• Дата: 28.03.2022
• Размер: 285.41 Kb.
• Имя файла: Э_1_Эконометр._Магистр.. — копия.docx
• Тип: Методические рекомендации; #421303
• страница: 2 из 9

Модель множественной регрессии.

1. Общий вид линейной модели множественной регрессии

Линейная модель множественной регрессии имеет вид:

, (1.1)

где y_p- расчётные значения исследуемой переменной, x₁, x₂, …, x_m - факторные переменные. Каждый из коэффициентов уравнения a₁, a₂, …, a_m имеет следующую экономическую интерпретацию: он показывает, насколько изменится значение исследуемого признака при изменении соответствующего фактора на 1 при неизменных прочих факторных переменных.

Фактическое значение исследуемой переменной тогда представимо в виде:

(1.2)

Для адекватности модели необходимо, чтобы случайная величина ε, являющаяся разностью между фактическими и расчётными значениями, имела нормальный закон распределения с математическим ожиданием равным нулю и постоянной дисперсией σ².

Имея n наборов данных наблюдений, с использованием представления (1.2), мы можем записать n уравнений вида:

, (1.3)

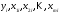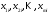где - значения исследуемой и факторных переменных в i-м наблюдении, а ε_i – отклонение фактического значения y_i от расчётного значения y_рi, которое может быть рассчитано с помощью (1.1) по значениям факторных переменных в i-м наблюдении.

Систему уравнений (1.3) удобно исследовать в матричном виде:

, (1.4)

где Yв – вектор выборочных данных наблюдений исследуемой переменной (n элементов), Xв – матрица выборочных данных наблюдений факторных переменных (n×(m+1)элементов), А – вектор параметров уравнения (m+1 элементов), а E – вектор случайных отклонений (n элементов):

1.5)

Оценка параметров модели с помощью МНК. Отбор факторов

При построении модели множественной регрессии возникает необходимость оценки (вычисления) коэффициентов линейной функции, которые в матричной форме записи обозначены вектором A. Формулу для вычисления параметров регрессионного уравнения методом наименьших квадратов (МНК) по данным наблюдений приведём без вывода:

(1.6)

При m = 1 соотношение (1.6) принимает вид (1.5).
Взаимосвязи объясняющих переменных – проблема мультиколлинеарности.

Мультиколлинеарность – это линейная взаимосвязь двух или нескольких объясняющих переменных. Наличие этого явления затрудняет анализ и определение вкладов каждой из переменных в объясняемое уравнение. Если некоторые или все объясняющие переменные в уравнении множественной регрессии сильно коррелируют друг с другом, то трудно разграничить их отдельное воздействие на результирующий Y .

При мультиколлинеарности коэффициенты нестабильны, значит ненадежны (например, значение R² высокое, но при этом величины ошибок велики, t-критерии малы). Следует различать два типа мультиколлинеарности: полная и частичная. Полная или совершенная присутствует, когда между объясняющими переменными модели существует линейная функциональная связь. На практике подобное встречается редко, поскольку на стадии отбора независимых переменных можно избежать появления мультиколлинеарности.

Частичная мультиколлинеарность возникает в случае достаточно тесных линейных связей между независимыми (объясняющими) переменными. Например, на розничную стоимость товара влияет его оптовая цена, объем грузоперевозок, стоимость грузоперевозок, где объем грузоперевозок и их стоимость – зависимые величины (с увеличением объема стоимость снижается).

Точных критериев по определению мультиколлинеарности нет, но есть рекомендации по выявлению мультиколлинеарности: необходимо проанализировать матрицу парных коэффициентов корреляции (ту часть, которая относится к объясняющим переменным):



Считается, если |r|>0,75...0,8, то это говорит о присутствии мультиколлинеарности. В случаях, когда имеется одна независимая и одна зависимая переменные, естественной мерой зависимости (в рамках линейного подхода) является корреляция между ними.

Нахождение параметров с помощью соотношения (1.6) возможно лишь тогда, когда между различными столбцами и различными строками матрицы исходных данных X отсутствует строгая линейная зависимость (иначе не существует обратная матрица). Это условие не выполняется, если существует линейная или близкая к ней связь между результатами двух различных наблюдений, или же если такая связь существует между двумя различными факторными переменными. Линейная или близкая к ней связь между факторами называется мультиколлениарностью. Чтобы избавиться от мультиколлениарности, в модель включают один из линейно связанных между собой факторов, причём тот, который в большей степени связан с исследуемой переменной.

На практике чтобы избавиться от мультиколлениарности мы будем проверять для каждой пары факторных переменных выполнение следующих условий:

(1.7)

То есть коэффициент корреляции между двумя факторными переменными должен быть меньше 0,8 и, одновременно, меньше коэффициентов корреляции между исследуемой переменной и каждой из этих двух факторных переменных. Если хотя бы одно из условий (1.7) не выполняется, то в модель включают только один из этих двух факторов, а именно, тот, у которого модуль коэффициента корреляции с Y больше.
Пример Будем считать, что торговое предприятие находится в г. N1, x₁ – температура воздуха в г.N1. Дополним данные наблюдений значениями факторной переменной x₃ – значениями температуры воздуха в г. N2 в период наблюдений:

y	x1	x2	x3
2	5,0	20	4
3,5	10,0	20	8
5	15,0	20	14
12	20,0	20	21
22	25,0	20	23
40	30,0	25	30
42	35,0	50	32

Проверим наличие мультиколлениарности между факторными переменными, произведём отбор факторов и найдём параметры линейной модели множественной регрессии. Для нахождения коэффициентов парной корреляции можно воспользоваться формулой (1.1). Поскольку вычисления будут достаточно громоздкими, эффективнее использовать средства табличного процессора Microsoft Excel. Применив к данным из Таблицы обработку Сервис/Анализ данных/Корреляция, получим набор коэффициентов парной корреляции Таблица*

	y	x1	x2	x3
y	1
x1	0,949	1
x2	0,723	0,690	1
x3	0,938	0,992	0,630	1

Проверим выполнение условий (1.7) для каждой пары факторных переменных.

Для x₁, x₂: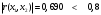

- выполняется,

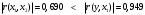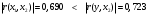- выполняется,

- выполняется.

Все три условия (1.7) выполняются, значит мультиколлениарность между факторными переменными x₁ (температура воздуха ) и x₂ (размер торговой наценки) отсутствует, то есть они могут использоваться в модели одновременно.

Для x₁, x₃: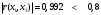

- не выполняется,

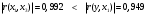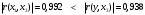- не выполняется,

- не выполняется.

Ни одно из условий не выполняется, следовательно, факторы x₁ (температура воздуха в г.N1) и x₃ (температура воздуха в г.N1) мультиколлениарны, то есть не рекомендуется использовать их в модели одновременно. Поскольку 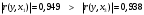, то фактор x₁ теснее связан с исследуемой переменной y (объём продаж), чем фактор x₃. Поэтому исключить из рассмотрения следует фактор x₃.

Для x₂, x₃: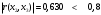

- выполняется,

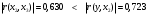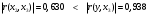- выполняется,

- выполняется.

Все три условия выполняются, значит мультиколлениарность между факторными переменными x₂ и x₃ отсутствует, и они могут использоваться в модели одновременно.

Можно резюмировать, что в модели можно оставить либо пару факторов x₁, x₂, либо пару x₃, x₂. То есть выбор необходимо сделать между факторами x₁ и x₃. Как уже отмечалось выше, фактор x₁ имеет преимущество, поскольку теснее, чем x₃, связан с y. Поэтому модель для объёма продаж y мы будем строить с учётом влияния факторов x₁ и x₂: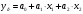

.

Для вычисления параметров модели по данным наблюдений выпишем вектор Yв и матрицу Xв:



Опуская операции транспонирования матрицы, перемножения матриц и нахождения обратной матрицы (можно воспользоваться в Excel функциями ТРАНСП, МУМНОЖ, МОБР), запишем промежуточный результат вычислений, необходимых для нахождения вектора параметров модели А по формуле (1.6):

.

Продолжая операции с матрицами в соответствии с (4.6), получим искомый вектор параметров модели:

.

То есть мы получили уравнение линейной регрессии следующего вида: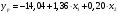

. (1.8)

Значения параметров модели указывают, что в среднем при увеличении температуры воздуха в г.N1 на 1 градус объём продаж на изучаемом предприятии увеличивается на 1,36 единицы, а при увеличении торговой наценки на 1% объём продаж увеличивается на 0,20 единицы. Последний вывод выглядит некорректно, поскольку в реальном процессе, наоборот, увеличение наценки сдерживает рост объёма продаж.

Определим по (1.8) расчётные значения исследуемой переменной для набора значений факторов, полученных в наблюдениях (Таблица *), и составим ряд отклонений ε_i фактических значений объёма продаж от расчётных значений.

Таблица 7

y	2	3,5	5	12	22	40	42
yр	-3,30	3,49	10,29	17,09	23,88	31,66	43,39
ε	5,30	0,01	-5,29	-5,09	-1,88	8,34	-1,39