Э_1_Эконометр._Магистр.. — копия. Методические рекомендации для выполнения задания стр. 3 Задание Изучение специальных методов построения регрессионных моделей
 Скачать 285.41 Kb. Скачать 285.41 Kb.
|
Косвенный метод наименьших квадратов (косвенный МНК).Рассмотрим на примере применение косвенного метода наименьших квадратов (косвенного МНК). Пример Пусть дана идентифицируемая модель из двух уравнений, содержащая две исследуемые и две факторные переменные:  . .Задан набор фактических данных:
Решение: Исходную модель можно преобразовать в приведённую форму модели вида:  . .Приведённая форма модели является системой независимых уравнений, к каждому из которых для нахождения коэффициентов можно применить МНК, подобно тому, как это делается для построения линейной модели множественной регрессии, состоящей из одного уравнения. Для нахождения коэффициентов первого уравнения мы применим в MS Excel обработку Cервис/ Анализ данных/ РЕГРЕССИЯ выбрав в качестве диапазона данных для исследуемой переменной колонку данных для y1, а в качестве диапазона данных для факторных переменных – колонки данных для x1 и x2. Аналогично для определения коэффициентов второго уравнения применим обработку РЕГРЕССИЯ, взяв данные для y1 , x1 и x2. В итоге получим следующую систему уравнений (ПФМ):  Для перехода от приведённой формы к структурной форме модели найдём x2 из второго уравнения: Подставим это выражение в первое уравнение вместо x2 , и после необходимых арифметических преобразований, получим первое уравнение структурной формы: Д 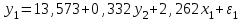 алее выразим x1 из первого уравнения ПФМ и подставим это выражение во второе уравнение ПФМ вместо x1. После очевидных преобразований получим второе уравнение структурной формы: 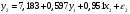 Окончательный вид структурной модели:  Задание 5. Цель и содержание задания Цель задания: изучение динамических моделей с коррелирующими факторами; модели с лаговыми зависимыми переменными 5.2 Методические рекомендации для выполнения задания Воспользоваться примером расчёта динамической модели, приведенным ниже. Содержание задания: Имеются данные об объёме валового внутреннего продукта Y некоторой страны в зависимости от инвестиций X в её экономику за 10 лет. Построить эконометрическую модель, используя метод Алмон, с распределённым лагом для l = 3 в предположении, что структура лага описывается полиномом второй степени. Общий вид исходной модели взять в форме: 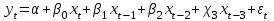 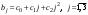 Исходные данные (yt,, xt) ( усл.. ед.) представлены в следующей таблице: Таблица
|
