методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов

• Название: Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
• Анкор: методические указания
• Дата: 19.09.2022
• Размер: 1.02 Mb.
• Имя файла: методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1.docx
• Тип: Методические указания; #685529
• страница: 19 из 19

 

 ³ 

_ 45

 ⁷⁰ 

После вводим значения остальных констант, полагая пока все коэффициенты регулято- ра m1,m2,m3, равными нулю.

T1 

T2  4

s 

0.4

k1 

2k2 

1.5

m1  0
m2  0

m3  0

Затем решаем дифференциальное уравнение, используя функ-
цию odesolve и строим график.

Give

T1T2

_d4 dt⁴
y(t)  (sT1T2  T1)

_d3 dt³
y(t) 

_d2 dt²

y(t) [T2  sT1  k1 k2 m2(a2  a3)]  [1  k1 k2 m1(a2  a3)] ^d

dt
y(t)  k1 k2 m3(a2  a3) y(t) 0

tk 
50y'''(0) 0

y(0) 0
y''(0) 0

y 
Odesolve(t  tk)

y' ( 0 ) 1

t 
0  tk

8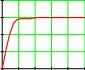
6
y( t) 4

2
0 10 20 30 40 50

t
Из графика видно, что система без регулятора устойчива , но имеет большую статиче- скую ошибку. Была проведена работа по подбору коэффициентов регулятора. В результате получено решение, показанное ниже.

m1  0.5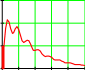

3
m2 
0.9
m3 

0.03

y( t)



2
1

0 10 20 30 40 50

t
Показаны значения подобранных коэффициентов и график переходного процесса. Порядок подбора рекомен- дуется следующий:

Сначала подбирается коэффициент пропорциональ- ного члена , в нашем случае –m1 , затем управление по скорости - демпфер, в нашем случае m2 , и в последнюю очередь -коэффициент интеграла –m3.

Следует иметь в виду , что большие значения коэффициентов m1 , m3 могут сделать систему неустойчивой.

2007

ЛИТЕРАТУРА

1. 
   Очков В.Ф. Mathcad 14 для студентов, инженеров и конструкторов БХВ - Петербург
   

2. 
   Очков В.Ф. Мультимедийный обучающий курс по Mathcad 13. Курс создан на фирме
   

Мультимедиа Технологии – [phone], www.mmt-dl.ru

3. 
   Интернет- форум exponenta.ru//Mathcad
   
4. 
   Демидович Б.П., Марон И.А. Основы вычислительной математики.
   

М.,»Наука»,Главная редакция физико-математической литературы.,1970

Турчак Л.И. Основы численных методов. М.,»Наука»,Главная редакция физико- математической литературы.,1987

5. 
   Беллман Р. Динамическое программирование. Издательство иностранной литерату- ры,М.1960
   
6. 
   Краснов А.Е. и др. Информационные технологии пищевых производств в условиях неопределенности. М.,2001
   
7. 
   Краснов А.Е. и др. Основы математического моделирования рецептурных смесей пищевой биотехнологии. М., Пищепромиздат ,2006
   
8. 
   Рутковский Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алго- ритмы и нечеткие системы. М., Горячая линия – Телеком,2007
   
9. 
   Грачев Ю.П. Математические методы планирования эксперимента. М., «Пищевая промышленность», 1979.
   
10. 
    Дэвис М.Х.А. Линейное оценивание и стохастическое управление. М.,»Наука», Главная редакция физико-математической литературы.,1984
    
11. 
    Ли Роберт. Оптимальные оценки, определение характеристик и управление.
    

М.,»Наука», Главная редакция физико-математической литературы.,1966