методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов

• Название: Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
• Анкор: методические указания
• Дата: 19.09.2022
• Размер: 1.02 Mb.
• Имя файла: методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1.docx
• Тип: Методические указания; #685529
• страница: 18 из 19

Проводим проверку значимости коэффициентов по Стьюденту:

Для этого:

7. 
   вычисляем выборочную и дисперсию и с.к.о.
   

8 3

  ^Y

• 
  MY _²
  

D 
i  1
j  1

i j i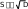
D  0.75
S  0.866

8238

7. 
   Вычисляем обратную функцию распределения Стьюдента для уровня значимости 0,95 и числа степеней свободы =16 Если в прямой функции распределения, задавшись значе- нием случайной величины и числом степеней свободы, мы вычисляем вероятность, то в об-
   

ратной функции, задавшись вероятностью и числом степеней свободы, мы получаем значе- ние случайной величины.

Для Стьюдента, как известно, число степеней свободы равно удвоенному числу экспе- риментов.

qt(0.95 16)  1.746

7. 
   Вычисляем доверительную ошибку ε и сравниваем ее с модулями значений коэф- фициентов.
   

qt(0.95 16)  1.746

  qt(0.95 16)S

  1.512

a^T  ( 81.875 0.625
4.375 13.125 9.375
1.875
4.375
1.875)
Мы видим, что второй

коэффициент меньше доверительной ошибки, следовательно, он не значим.

7. 
   Записываем уравнение регрессии без учета второго коэффициента:
   

Q1  a  a  X

 a  X  a  X

 a  X  a  X

 a  X

i 1 3

i 2 4 i 3

5 i 4 6 i 5

7 i 6 8 i 7

Проверка адекватности по Фишеру

7. 
   Вычисляем функцию F.
   

^{ 8} _ Q  MY

_2_
SAD

SAD  ^_

i i _

F 


 12

 ₁ 

D SAD  4.105 10

_i  1 _

F  5.473

 12

10

7. 
   Вычисляем обратную функцию распределения Фишера:
   

qF(0.95 16 1)  246.464

7. 
   Так как Вычисленное F < qF, то с вероятностью 0,95 полученное уравнение адек- ватно экспериментальным данным.
   

ЛАБОРАТОРНАЯ РАБОТА №18. АДАПТИВНЫЙ ФИЛЬТР КАЛМАНА

Основной проблемой, возникающей при любых измерениях, является их недоста- точная точность. Имеется два пути решения этой проблемы: повышение точности изме- рительных приборов и повышение точности путем статистической обработки избыточно- го числа измерений, в результате которой получают оценку измеряемой величины. Повы- шение точности измерительных приборов требует существенных затрат, в то время как статистическая обработка измерений при наличии компьютера стоит дешево и проводит- ся достаточно быстро.

Сегодня существует множество методов статистической обработки измерений. Их можно разделить на два больших класса: просто статистической обработки и опти- мальной обработки, в результате которой получают в каком- то смысле оптимальную оценку измеряемой величины. Кроме того, обычно разделяют методы статистической обработки для статических и динамических систем. Статистическая обработка статиче- ских систем изучалась на 4-м курсе. Это метод наименьших квадратов. Мы ниже рас- смотрим несколько методов оптимальной статистической обработки информации дина- мических систем на конкретных примерах.

Сложность обработки информации в динамической системе заключается в том, что ее состояние ме- няется во времени и отдельные измерения переводить из одного состояния в другое.

Существует также несколько методов оптимальной статистической обработки для динамических систем. Это фильтры Винера, Винера- Хопфа и др.

В 1961 году американский математик КАЛМАН разработал оптимальный фильтр для линейных нестационарных систем. Преимуществом фильтра Калмана является то, что он решает задачу во временной , а не частотной области, как , например, фильтр Винера.

Калман разработал свой фильтр для многомерных задач Формулировка задачи , как правило, задается в матричной форме, однако мы рассмотрим ниже простейшие скалярные задачи. в матричной форме

Фильтр Калмана существует в непрерывной и в дискретных формах. Разберем дис- кретный фильтр Калмана.

Рассмотрим следующую задачу

Блок- схема исследуемого процесса имеет вид: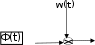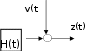
f(t)

y(t)

x(t)

Рис.1. Блок – схема объекта.

. Здесь Ф – линейный объект( т.е. объект описываемый линейными соотношениями), на выходе которого вырабатывается неслучайный сигнал y(t). На выходную величину воз- действует аддитивный (в виде слагаемого ) шум w(t). Шум w(t) – это какие –то случайности внутри нашей системы. После шума мы имеем выходную величину x(t). X(t) – выходной сигнал нашей системы есть сумма неслучайного процесса y(t) и шума. Поэтому это уже случайный процесс. Поэтому в целом наша система – вероятностная ( стохастическая). Мы хотим определить неизвестный нам случайный выходной процесс y(t) измерить неслучайную выходную величину y(t), но измеряем мы не ее, и не случайный выходной сигнал системы x(t), а преобразованный линейным блоком Н случайный процесс z(t). Это так называемые косвенные измерения, когда меряется какая – то функция определяемой величины. В общем случае Ф и Н могут изменяться во времени.

Шумы W(t) и v(t) – нормально распределенные случайные процессы с нулевыми математическими ожиданиями,

M(w)=0

M( v) =0 и с постоянными дисперсиями Q и R, соответственно.

Процесс x(t) также распределен нормально , т.к. любое линейное преобразование нор- мально распределенного процесса есть нормально распределенный случайный процесс, а шум w(t) подчиняется нормальному закону распределения. Измерения производятся с ошибкой v (t) .

Таким образом, в действительности мы измеряем величину

z(t)=H(x(t)+W(t))+v(t)

, (1)

причем случайный процесс z ( t) также распределен нормально.

оценку

Требуется построить фильтр, после которого мы получим наилучшую

y^{ˆ величины y.}

^{Каждое последующее состояние системы определяется предыдущим:} x_k+1 =x_ke

–∆t

T _.

Нижеприведенная программа составлена для Q=R=0.1. Для оценки качества фильтра- ции в программе решается также уравнение незашумленного, якобы «неизвестного» нам процесса.

Программа решения данной задачи в Маткаде приведена на рис.2 Здесь: y-«незашумленная» переменная,

X1- оцениваемая переменная:

Z 

y  0

x1  0

Q  0.1

R  0.1

z  dnorm^rnd^2 _{P } QR

Q  R

_{x1 } Qz  Rx1

Q  R

T  5


Q^ y


Q^  dnorm^rnd^2


R^ 0 R^
Z- измеряемая переменная.

В доцикловой части первым опе- ратором присваивается начальное зна- чение «незашумленной» и оценивае- мой переменной, причем начальное значение оцениваемой переменной бе- рется «с потолка», вводятся постоян- ные значения дисперсий обоих шумов и постоянной времени системы, про- изводится первое измерение z и вы- числяется первая оценка мат. ожида-

_for



k  1 100
_ 1 _
 1 <sub>

</sub> ния и дисперсии.

^ Измерение рассматривается как

_ x1  1  exp

_{ } T

 ²

• 
  x1exp
  

  ^T 

^ сумма двух псевдослучайных величин,

^ каждая из которых образуется с по-



 P  P 



P


P  Q  R

_ мощью двух функций:

_ Функция r n d (x) возвращает

^ y  1  exp^{ 1 }  yexp^{ 1 }

_ равномерно распределенное случайное

^  ^T 



^ z  dnorm^rnd^2



^ _{x1 } (Pz  Rx1)

_ P  R
Q^ y

 ^T 

Q^  dnorm^rnd^2
R^ 0





R^ _







число в диапазоне 0 –x.

Функция d n o r m ( x,y,w) воз- вращает нормально распределенное псевдослучайное число для аргумента x, с математическим ожиданием y и

^ P  P




Z


^  z

k

R

P  R

_ с.к.о z.

_ В первой функции dnorm за мат.

^ ожидание принято значение y – «не-

^ зашумленной» переменной, во второй

 <sub>Y

</sub> k

^ X1

 y

 x1

^ – мат. ожидание равно 0.



^ В цикловой части программы

 ^k 

 ^k 

Z

производится перевод оцениваемых переменной и дисперсии в новое со- стояние системы, затем переводится в новое состояние «незашумленная» пе

Рис.2. Программа фильтрации фильтром Калмана

X1 _j

Y_j Z _j



2.5
2.22
1.94
1.67
1.39
1.11
0.83

j  0 100

ременная , производится новое измерение z и вы- числяется новая оценка оцениваемой переменной и дисперсии. В последних операторах цикловой части производится накапливание измерений, оцениваемой и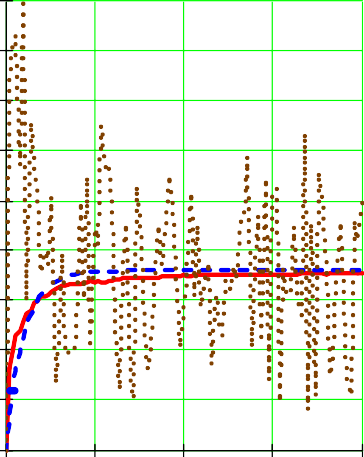

«незашумленной» переменной в массивы, с це- лью вывода их на печать после окончания решения

На рис.3. приведены решение задачи. Кривая, изо- браженная штрихом – «незашумленная» переменная, непрерывная кривая – оценка, точечная кривая – изме- рения без фильтрации.

0.56

0.28


0 25 50 75 100

j
Рис.3. Графики кривых

око

ЛАБОРАТОРНАЯ РАБОТА № 19. ПОДБОР ПИД РЕГУЛЯТОРА

Система автоматического управления задана своей структурной схемой

(рис.1) и данными, приведенными в таблицах.

Необходимо: Задавшись данными из таблиц 1,2, стабилизировать движение системы

+

+

σ

ло выбранной траектории, подобрав коэффициенты ПИД - регулятора.

Данные для выбора ПИД – регулятора:

Здесь звенья 1 - 4 описывают объект управления, а звено 5 - регулятор.

По исходным данным отдельных звеньев, сведенным в таблицу, следует составить уравнение системы и провести подготовку ее имитационного моделирования на ЭВМ в па- кете МАТКАД. Само моделирование будет проведено на лабораторных занятиях.

Цель моделирования - подбор закона управления в звене 5, подбор ПИД- регулятора. 1.Звено 1 - линейное динамическое и описывается дифференциальным уравнением 2-го

порядка:

T₁² dy₁ ²/ dt² +₁T₁dy₁/dt +y₁ = k₁

2. 
   Звено 2 - линейное статическое, зависимость выхода от входа y ₂ (y₁) задана табли- цей. Для ввода в ЭВМ необходимо найти аналитическую функциональную зависимость y₂(y₁) , проведя аппроксимацию.у₂=а₂у₁
   
3. 
   Звено - также статическое, зависимость выхода от входа y ₃ (y ₁) также задана табли- цей. Однако, из-за неточных измерений аппроксимацию следует проводить линейной регрес- сией, вычислив коэффициенты уравнения y ₃= a₃ y ₁ .
   
4. 
   Сигналы y ₂ и y₃ складываются в сигнал  =y₂ +y₃.
   

5 .Звено 4 - линейное динамическое и описывается передаточной функцией

T₂dy/ dt +y = k ₂  .

6.Структура закона управления задана

y₅ = ₁ y +  ₂ dy /dt + ₃ y dt
Составим уравнение всей системы. Для этого: Выпишем все уравнения

T² y``Ty` y k

1 1 1 1 1 1

y₂  a₂ y₁ y₃  a₃ y₁

  y₂  y₃ T₂ y` y k₂

t

 m₁ y m₂ y`m_{3 } ydt

0

Так как мы будем решать задачу при нулевом входном сигнале, то ∆= -y5, что позволя- ет объединить уравнения 1 и 6:

t

1 1 1 1 1 1 1 2 3 _

T² y``Ty` y k(my my`m ydt

0

Объединим уравнения 2-4. Получим

  (a₂  a₃ ) y₁

Запишем уравнения 1 и 5 в операторной форме.

T² p²  Tp1) y k(m mp m¹ ) y

1 1 1 1 1 2 3 _p

(T₂ p1) y k₂ (a₂  a₃ ) y₁

Чтобы освободиться от интеграла продифференцируем первое уравнение

(T² p³  Tp²  p) y k(mp mp²  m) y

1 1 1 1 1 2 3

Разрешим второе уравнение относительно у1:

_y (T₂ p1) y

¹ k(a a)

ли:

2 2 3

Подставим теперь это выражение в уравнение, которое мы продифференцирова-

(T² p³  Tp²  p) ₂

^{1 1} (T₂ p1) y k₁(m₁ p m₂ pk₂ (a₂  a₃ )

• 
  m₃ ) y
  

Освободимся от знаменателя и сделаем приведение подобных:

(T² p³  Tp²  p)(Tp1) y kk(mp mp²  m)(a a) y

1 1 2 1 2 1 2 3 2 3

[(T² p³  Tp²  p)(Tp1)  kk(mp mp²  m)(a a)]y 0

1 1 2 1 2 1 2 3 2 3

{T²Tp⁴  (TT T²⁾ ) p³ [T T kkm(a a)] p²  [1 kkm(a a)] p kkm(a a)}y 0

1 2 1 2 1 2 1 1 2 2 2 3 1 2 1 2 3 1 2 3 2 3

Перейдем во временную область

₂ d⁴ y ₂₎ d³ y d² y dy

T₁ T₂

dt⁴

 (T₁T₂  T₁

⁾ dt³

[T₂  T₁  k₁k₂m₂ (a₂  a₃ )] _dt2

[1 k₁k₂m₁ (a₂  a₃ )] _dt k₁k₂m₃ (a₂  a₃ ) y 0

Мы получили однородное дифференциальное уравнение четвертого порядка, ко- торое и будем моделировать

Решение задачи в Маткаде.

1. 
   Пусть по таблице 1 выбрано k ₁= 2 , k ₂=1,5, T₁ = 5, T₂= 4,  ₁= 0,4 , а из таблицы
   

y1	0	1	2	3
y2	25	47		-
y3	11. 4	46	45	70

2 -

2. 
   По данным таблицы составим векторы vx2,vy2,vx3,vy3.Используя встроенную функцию line определим коэффициенты a2,b2,a3,b3. (см.рис.1)
   

vy2 

_ 28 _

 ¹⁷ 

_yvx2 

2

 ⁰ 

 ¹ 

a2 

slope(vx2 vy2)

a2  11

 ⁰ 

 <sub>1

</sub> 14 _
a3 
slope(vx3 vy3)

a3  16.7

^{vx3 }  

_ 2
vy3 

^ 46