методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов

• Название: Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
• Анкор: методические указания
• Дата: 19.09.2022
• Размер: 1.02 Mb.
• Имя файла: методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1.docx
• Тип: Методические указания; #685529
• страница: 12 из 19



i  0

_

^{j  1}

_B_j_ M1 _i

 B_j10 M1

_i  B_16 

POS1 _i 0



Была как можно ближе к нулю.

На рис.6.показаны значения подобранных компьютером коэффициентов.

Проверка адекватности полученного решения.

После решения получаем значения подобранных коэффициентов в векторе В.

Подбор коэффициентов осуществлялся по опорным значениям аргументов (матрица М1).Теперь необходимо проверить, какова разница между экспериментальными значения- ми функции П.О.С. и теоретическими, подсчитанными по созданной формуле. Сначала по- считаем ошибки относительно опорных точек. Ведь даже и через них теоретическая функция точно не проходит. Программа подсчета приведена на рис. 7. Здесь именем POSEX обо- значена выбранная модель. Из рисунка видно, что максимальная абсолютная ошибка со- ставляет около 14 единиц, а максимальная относительная ошибка – около 11 %, что терпимо.

i  0  length^POS1^{1 }  1

POSEX_i 

5



j  1

^B_j^^M1_{i j}
^Bj5

 B_j10M1_{i j}  B <sup>


16</sup>
max^1^



 12.652

_i 

POSEX_i  ^POS1^{1 }

max^^
 14.058
_i

i

max(delta)
 11.429 %

delta_i 

max^POS1

₁ _

max(delta1)

 10.122 %

Рис. 7. Программа определения ошибок расчета опорных точек.

¹⁶
Затем посчитаем ошибки определения контрольных точек (см. рис.8). i  0  10

POSKEX_i 

5



j  1

^B_j^^M2_{i j}

^Bj5

 B_j10M2_{i j}  B ^

1_i 

POSKEX_i  ^POSK^{1 }


i
1_i

delta1_i 

max^POSK

₁ _

Рис.8. Расчет ошибок определения контрольных точек.

Видим, что и в этом случае максимальная относительная ошибка составляет около 10%.

Делаем вывод: созданная модель работоспособна и может с достаточной достоверно- стью быть использована для расчетов.
ЛАБОРАТОРНАЯ РАБОТА № 10. НЕЧЕТКИЕ МНОЖЕСТВА.

Построение функций принадлежности. Как известно, принадлежность элемента дан- ному нечеткому множеству определяется его функцией принадлежности. Ниже приведены примеры задания некоторых функций принадлежности .

Для задания функции принадлежности используется функция Маткада IF (ЕСЛИ). В этой функции первое выражение – условие, в данном примере – это x1<=1, второе число – значение функции при выполнении условия – в примере это 0, третье число – значение функ- ции при невыполнении условия. В примере – это 0.5*(x1-1).График функции принадлежно- сти приведен на рисунке для x1, меняющегося от 0 до 5.

11 ^x1^  if ^1 ^x1^  1  1 ^x1^  0^

(x)  if [5  x  0  if [7  x  0.5  (x  5)  if [12  x  1  if [16  x  1  0.25  (x  12)  0]]]]

^1 ^x1 _i
4.5

3.375

2.25

1.125



0 2.5 5 7.5 10

x1 _i

1

0.4

^2 ^x1 _i ^{ 0.2 0 2}

 0.8

 1.4

 2


4 6

x1 _i


8 10

Ниже на рис.1 приведены другие функции принадлежности и построены их графики. Если теперь присвоить х какое либо конкретное значение, то можно определить веро-

ятность принадлежности этого значения тому или иному множеству. Например, положив х1=5, получим 1(х1)=2, 2(х1)=0.1и т.д.

Напоминаем, как выполняется функция IF: сначала записывается условие, затем через запятую, чему равно , если это условие выполняется, затем, снова через запятую, чему рав- но  в случае невыполнения условия. Следовательно, формула выполняется так:

Если 5>x, то  равно 0. В противном случае, если 7> x=>5,  =0.5(x-5). В случае, если

12>x=>7,  =1. И, наконец, если 16>x=>12, то  =1-0.25(x-12), а если 16<=x, то =0

i  0  100
x1_i  0.1  i

1 ^x1^  if x1  1  0  0.5  ^x1  1^ 2 ^x1^  if x1  2  1  0.3  ^x1  2^  1

^11 ^x1_i

1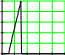

0.8

0.6

0.4

0.2


0 2 4 6 8 10

x1_i

 x_i


1
0.75
0.5
0.25

0 4

8 12 16 20

x_i

Рис.1. Построение различных функций принадлежности в Маткаде.
Задача 1. Построить в Маткаде приведенные выше функции принадлежности и их гра- фики. Вычислить в Маткаде значения всех функций принадлежности для х1=0,1,2,5,10.
Задача 2.Операции над нечеткими множествами. В теории множеств определены операции пересечения и объединения множеств. Пересечением ^ABдвух множеств А и В

называется множество, элементы которого принадлежат как множеству А, так и мно- жеству В. Объединением ^ABдвух множеств А и В называется множество, элементы ко- торого принадлежат ИЛИ множеству А ИЛИ множеству В. Для нечетких множеств, конеч- но, также существуют эти операции. Однако при этом меняются их функции принадлежно- сти.

Если новое множество является пересечением двух нечетких множеств, его функция принадлежности является минимумом из функций принадлежности каждого из первона- чальных множеств. Ниже приведены на одном графике функции принадлежности двух не- четких множеств, а рядом приведена функция принадлежности пересечения этих множеств, полученная как минимум каждого из двух исходных множеств.

3 ^x1^  min^11^x1^ 21^x1^

1

0.8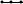

^11 ^x1_i _0.6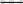

^21 ^x1_i _0.4

0.2

0 2 4 6 8 10

x1_i
0.8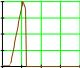

0.6

^3 ^x1_i _0.4


0.2


0 2.5 5 7.5 10

x1_i

Рис.3 Функция принадлежности пересечения двух множеств.

Функция принадлежности объединения двух нечетких множеств строится как макси- мальное значение функций принадлежности каждого из объединяемых множеств. Ниже на рис.4 приведены формула и график функции принадлежности объединения двух нечетких множеств, показанных в левой части рис.3.

Задание 2. Провести построение всех приведенных выше функций принадлежно сти и графиков

4 ^x1^


 max
_ 11 ^x1^ _

 

1

0.8


 
0.6

4 x1_i

0.4

_ 21 x1 _

0.2
0

2 4 6

x1_i

Рис.4. Функция принадлежности объединения двух множеств.

.