методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
 Скачать 1.02 Mb.
|
|
500 gi bj if d d1 if d d1 и содержание белка от 5 также до 30%. Каждый из этих участков мы делим на 500 отрезков и вычисляем значе- ние вкуса для каждого сочетания значений жира и белка, т. е. g=10, b=5; g=10,b= 5.05; g=10,b=5.1;….g=10.04,b=5;g=10.04,b=5.05….. и т.д. Вы- численное значение вкуса – d ( начальное значение d = 0) мы сравниваем с предыдущим и запоминаем в векторе G={G0, G1, G2} все вычисленные величины только в том d d1 G 0 d i j G if d d1 случае, если новое значение d больше предыдущего. В вычисленном векторе G первый элемент – максимальное значение функции, второй – оптимальное с точки зрения экспертов содержание жира, а третий – оптимальное со- держание белков в молочной колбасе. Рис.5. Программа вычисления максимума трехмерной функции принадлежности 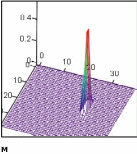 i 0 40b1 5 j 0 40 b2 20 g2 20 g1 10 b b1 ( b2 b1) j j 40 M gbg b (g2 g1) i gi g1 40 i j i j Рис. 6. График трехмерной функции принадлежности. ЗАДАНИЕ 1. Внимательно разобраться в изложенном выше материале. Пользуясь из- ложенным материалом, решить задачу. ЛАБОРАТОРНАЯ РАБОТА №12. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО МИНИМУМУ РАССТОЯНИЯ Если заданы два многомерных вектора v и w , то расстояние R между ними будет оп- ределяться в скалярной или матричной форме по формулам: 3  5 1 10 R 7.81 w 2 v 6 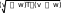 8 4 R 7.81 Условие задачи. Даны три группы частотных спектров по четыре спектра в каждой группе бензинов: бензина А-76, бензина АИ-95 и бензина АИ-98. Поступает спектр неизвестного бензина. Нужно вычислить «расстояния» от этого спектра до каждого из заданных, найти минимальное, и отнести поступивший бензин к той марке, расстояние до одного из спектров которой минимально. Решение. Перед началом решения командой файл- настройка страницы зададим альбомный формат ( landscape). Все спектры расположены в папке Маткад- данные для лаб. работы. В ней созданы три папки для известных марок бензина и папка « неизвестных» спектров. Для начала счета с единицы введем ORIGIN: =1 Сначала необходимо ввести все известные (опорные) спектры в Маткад. Это произ- водится с помощью команд меню- вставить-данные-ввод файла. После ввода этих команд открывается окно file options (опции файла), в котором имеется кнопка « browse» (искать). Нажав на эту кнопку, откроем окно read from file (читай из фай- ла) и укажем путь: Маткад-данные для лаб. Работы- бензин А-76- спектр1.Потом нажмем кнопку открыть. Затем нажмем два раза кнопку готово в окне file options. В Маткаде появится рамка с надписью А-76 …….txt. Присвоим ему имя F11. Аналогично введем остальные спектры бензина А76, присвоив им имена F12, F13, F14, и все спектры бензинов АИ-95, присвоив им имена F2i, и все спектры бензина АИ-98, при- своив им имена F3i.Здесь индексы i меняются от 1 до 4. Ввод данных закончен.
3 . Введенные спектры представляют собой матрицу из 7462 строк и 3 столбцов: пер- вый столбец – порядковый номер, второй – частота и третий – амплитуда спектра S1 Рис.1 Вид части одного из введенных спектров. Нас интересует только амплитуда. Поэтому сформируем из амплитуд всех введенных спектров три матрицы из четырех столбцов каждая: для бензина А-76 матрицу S1, для бен- зина АИ-95 матрицу S2 и для бензина АИ-98 матрицу S3. Cначала введем заголовок «Формирование матриц». Для этого нажав одновременно кнопки shift и Э ( в английском шрифте), откроем окно надписей. Перейдя на русский и вве- дя в меню шрифт Arial cyr, запишем этот заголовок. Формирование матриц Затем сформируем сами матрицы как показано на рис.2. Цифра или буква в уголках в показателе матрицы обозначает соответствующий столбец данной матрицы. i 1 4 i i S1 F1 3 F2 i 3 i i S3 F3 3 i S2 Рис.2 Формирование матриц.
F1 1 Рис.3. Матрица S1. Спектры введены в формате текстов (Это видно из того, что каждое число записано в кавычках) . Их следует перевести в цифровой формат с помощью встроенной функции str2num. (string – строка, num- число). Перевод показан на рис.3 k i k i k 1 7462 str2num S1 k i S1 S2(k i) str2numS2 S3 str2numS3 k i k i Рис.4. Перевод текстовых файлов в цифровые. Подготовим «неизвестные» спектры. На самом деле спектры, которые мы называем «неизвестными» нам известны. Первый из этих спектров принадлежит бензину А-76, второй – бензину АИ-95, третий – бензину АИ-98. Мы должны проверить, правильно ли распознает их формируемая нами программа. X X  X1 2 3 j Y X 3 j Y str2numY j 1 3 k j k j  Введем «неизвестные» спектры, как мы это делали для известных спектров, дав им имена X1, X2, X3,выделим третьи столбцы и переведем их в цифровую форму ( см.рис.5).K for j 1 3 Составим программу поиска мини-  min1 min 2 min 3 for k 1 4 мального расстояния между каждым из 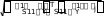 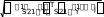 «неизвестных» и всеми известными спек- трами ( см рис.5 ).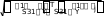 Так как у нас три «неизвестных» спектра, то мы организуем цикл по j от 1 до 3.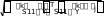 Переменными min1,min2,min3 мы обозначим минимальные расстояния до спектров бензинов А-76, АИ-95 и АИ-98, 1k соответственно. В начале мы присвоим им значения расстояний от «неизвестных» min 1 1k if 1 min 1 спектров до первого из спектров каждой группы. k 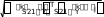 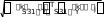 2k 9. В каждой марке бензинов мы име- min 2 2k if 2 min k 2 ем четыре известных спектра. Поэтому ор- ганизуем цикл по «к» от 1 до 4-х. В этом цикле мы ищем минимальные расстояния 3k от каждого из «неизвестных» спектров до min 3 k 3k if 3 min k 3 спектров каждой марки. Эти вычисленные минимальные расстояния циклом по «i» мы помещаем в j MIN min 1 вектор MIN. Следующим циклом по «i» мы по-  forfor i 1 3 j MIN min i i i 1 3 if MINj min i мещаем в вектор «К» условный номер марки бензина. Группа 1 – бензин А-76, группа 2 – бензин АИ-95, группа 3 – бензин АИ-98. Наконец, для большей наглядности  Kj i iKj "76" Kj "95" if MIN min  j i  if Kj 1 if Kj 2 "76" K "95"  "98" присваиваем группе 1 имя «76», а осталь- ным, соответственно, имена «95», «98». ниже приведен вектор ответа. Ви- дим, что распознавание произведено пра- вильно. Kj "98" j K if Kj 3 Рис.5 Про- грамма определения марки бензина. |