методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
 Скачать 1.02 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО КОЛИЧЕСТВА ЖИРА И БЕЛКОВ В МОЛОЧНОЙ КОЛБАСЕ. Использование нечетких множеств. Согласно техническим условиям молочная колбаса высшего сорта должна содержать: Жира: 13,5 -15,5 %, Белков: 14,6 – 15,4%. Нескольким дегустаторам было поручено определить наиболее предпочтительное вкусовое содержание этих составляющих в заданных т.у. пределах. При этом от них требовалась следующая четырех балльная оценка: Вкусно – 1, Скорее вкусно, чем невкусно – 0.8, Скорее невкусно, чем вкусно – 0.3, Невкусно – 0. После статистической обработки (определялось среднее арифметическое их ответов) были получены матрицы оценок, приведенные на рис.1 1 13.5 13.83 0 0.34 14.17 0.67 14.5 14.83 1 0.67 15.16 15.5 0.34 0 2 14.6 14.73 1 1 14.87 15 15.13 1 1 0.62 15.27 15.4 0.31 0 для белков для жира Рис.1. матрицы оценок содержания жира и белков в молочной колбасе. Здесь в первой строке – процентное содержание жира или белков, а во второй – оцен- ка вкуса колбасы экспертами. На основании мнений дегустаторов нужно определить оптимальное соотношение жира и белков в молочной колбасе. 1. Сначала составим аналитические зависимости для обеих матриц. Каждая матрица является нечетким множеством, поэтому мы будем опрделять для них функции принадлежности. Рассмотрение первой матрицы показывает, что она хорошо ап- проксимируется нормальным законом распределения (x M[x])2 y=e σ2 где M[x] – математическое ожидание случайной величины x, 2 –ее дисперсия, а С – константа. Мы обозначим y как g(g,A1,B1), где g- значение случайной величины, А1- вели- чина, обратная дисперсии, В1- математическое ожидание. Имеем: A1(B1g) 2 g g A1 B1 e . (1) Численные значение В1 определим как среднее арифметическое нулевой ( счет в Мат- каде начинается с 0) строки матрицы жира, а численное значение А1 – как статистическую дисперсию этой строки. В Маткаде среднее арифметическое вычисляется функцией mean ( v), где v – вектор- столбец, а статистическая дисперсия функцией stdev (v). У нас же имеется строка, а не столбец. Поэтому введем вспомогательный вектор –строку v1, которую потом транспонируем. В формуле (2) каждому элементу вектора – столбца v1 присваивается зна- чение соответствующего элемента нулевой строки матрицы жиров: v1i 1 0 i . (2) Затем вычисляем эти значения, транспонируя вектор – строку v: . B1 meanv1T A1 1 T2 B1 14.499 Здесь т – индекс транспонирования. stdev v1 A1 2.256 График полученной функции принадлежности на рис.2 показывает, что она хорошо ап- проксимирует экспериментальные точки.  g 12 12.1 18i 0 6 1  0.8 g (g A1 B1) 0.61 1 i  0.4 0.2 12 13.2 14.4 15.6 16.8 18 g 1 0 i Рис.2 . График аналитического выражения для функции принадлежности жира. Рассмотрим теперь вторую матрицу рис.1. Мы видим, что левая часть ее второй строки является константой, а правая примерно подчиняется нормальному закону. По-видимому, при аппроксимации функции принадлежности аналитическим выражением логично задаться для левой части единицей, а для правой – нормальным законом распределения. Для определения параметров нормального закона составим симметричную вспомога- тельную матрицу µ20, приведенную на рис.3. 20 14.6 14.73 14.87 15 15.13 15.27 15.4 0 0.31 0.62 1 0.62 0.31 0 Рис.3. Вспомогательная матрица Повторяя все действия, проведенные для матрицы µ1, определим параметры нормаль- ного закона распределения для матрицы µ20: 1.Зададимся законом распределения b0(b A2 B2) expA2(B2 b)2 где b – количество белков в колбасе, сформируем вспомогательный вектор v2 и найдем значения коэффициентов А2 и В2:, i 0 6 v2i 200 i A2 1  2 stdev v1T B2 meanv1T A2 14.011 B2 15 Теперь создадим аналитическое выражение для функции принадлежности матрицы белка, назвав ее (b,A2,B2) . Введем после функции принадлежности для белков последова- тельность чисел b и используем условный оператор Маткада IF. (b A2 B2) if b 15 1 b(b A422 B2) Если b меньше или равно 15, то функция принадлежности равна 1, в противном случае она равна вспомогательной функции. График полученной функции принадлежности и аппроксимируемые точки приведены на рис.4. 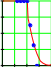 1 (b A2 B2) 21 k   0.75 0.5 0.25 0.998 G 14.48 14 14.5 15 15.5 16 b 20 k 14.8 Рис.4 График аналитического выражения функции принадлежности для белков Для определения оптимального содержания и жиров и белков в колбасе нам нужно найти теперь пересечение обеих функций принадлежности и определить максимум новой, трехмерной функции принадлежности. Пересечение ищем в виде функции двух переменных µgb (g,b), используя функцию Маткада min. gb(g b) min g(g A1 B1) b(b A2 B2) Трехмерный график новой функции принадлежности и его построение представлены на рис.6. Функция (g,b) показывает, как по мнению дегустаторов, вкус колбасы зависит от со- держания белка и жира. Естественно, мы хотим определить такое количество жира и белков в колбасе, чтобы она была как можно вкуснее, т.е. определить максимум этой функции.  Для нахождения максимума этой функции, т.е. оптимального с точки зрения экспертов G d 0 содержания жира и белков в молочной колбасе, составим for i 0 500 for j 0 500 небольшую программу, приведенную на рис.5. Для нахождения максимума мы , исходя из графика функции, рассматриваем содержание жира от 10 до 30% |
