методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов

• Название: Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
• Анкор: методические указания
• Дата: 19.09.2022
• Размер: 1.02 Mb.
• Имя файла: методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1.docx
• Тип: Методические указания; #685529
• страница: 16 из 19

ЛАБОРАТОРНАЯ РАБОТА № 14. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО НЕЧЕТКОЙ МЕРЕ СХОДСТВА.
В работах А.Е. Краснова разработано положение об оптимальных мерах сходства. Та- кой мерой является, например, выражение, приведенное на рис.1.



  ^

_j _k _^T _ _j _k _

Y  S31  Y  S31
Рис.1 Оптимальная мера сходства.

 _j

Здесь  и  константы, ^Y

_k

неизвестный спектр, ^S31

• 
  один из известных спектров. Т –
  

индекс транспонирования вектора.

Чем больше мера сходства, тем больше связь между двумя векторами.

Условие задачи.

Даны три группы частотных спектров по четыре спектра в каждой группе бензинов: бензина А-76, бензина АИ-95 и бензина АИ-98.

Поступает спектр неизвестного бензина. Нужно вычислить меру сходства между неиз- вестным спектром и каждым из заданных, найти максимальную и отнести поступивший

бензин к соответствующей марке.

Решение.

Перед началом решения командой файл- настройка страницы зададим альбомный

формат ( landscape).

Все спектры расположены в папке Маткад- данные для лаб. работы. В ней созданы три папки для известных марок бензина и папка « неизвестных» спектров.

1. 
   Для начала счета с единицы введем ORIGIN: =1
   
2. 
   Сначала необходимо ввести все известные (опорные) спектры в Маткад. Это произ- водится с помощью команд меню- вставить-данные-ввод файла. После ввода этих команд открывается окно file options (опции файла), в котором имеется кнопка
   

« browse» (искать). Нажав на эту кнопку, откроем окно read from file (читай из фай- ла) и укажем путь: Маткад-данные для лаб. Работы- бензин А-76- спектр1.Потом нажмем кнопку открыть.

Затем нажмем два раза кнопку готово в окне file options. В Маткаде появится рамка с надписью А-76 …….txt. Присвоим ему имя F1₁.

Аналогично введем остальные спектры бензина А76, присвоив им имена F1₂, F1₃, F1₄, и все спектры бензинов АИ-95, присвоив им имена F2_i, и все спектры бензина АИ-98, при- своив им имена F3_i.Здесь индексы i меняются от 1 до 4.

Ввод данных закончен.

3 . Введенные спектры представляют собой матрицу из 7462 строк и 3 столбцов: пер- вый столбец – порядковый номер, второй – частота и третий – амплитуда спектра ( см. рис.2)

1:	399.95	-0.000131
2:		400.44	0.001253
3:		400.92	0.001301
4:		401.40	0.000805
5:		401.88	0.000681
6:		402.37	0.001579
7:		402.85	0.003724
8:		403.33	0.006809
9:		403.81	0.010327

Рис.2 Вид введенного спектра.

Нас интересует только амплитуда. Поэтому сформируем из амплитуд всех введенных спектров три матрицы из четырех столбцов каждая: для бензина А-76 матрицу S1, для бен- зина АИ-95 матрицу S2 и для бензина АИ-98 матрицу S3.

Cначала введем заголовок «Формирование матриц». Для этого нажав одновременно SHIFT и Э ( в английском шрифте), откроем окно надписей. Перейдя на русский и введя в меню ARIAL CYR, запишем этот заголовок.

j  1 3

Затем сформируем сами матрицы как показано на рис.3.

i

i

i
K 

for

i  1 4 j  1 3

  10

_i

S1

 _F1 _

₃

_i

S2

 _F2 _

₃

_i

S3

 _F3 _

₃

Рис.3 Формиро-

  0.01

max  0

1

max  0

2

max  0

3

вание матриц.

4. 
   Спектры введены в формате тек- стов. Их следует перевести в цифровой формат с помощью встроенной функ- ции str2num. (string – строка, num- чис- ло). Перевод показан на рис.4.
   

for k  1 4

1_k ^

k  1 7462

  ^

_j

_k _^T _

_j

_k _

S1 _

 str2num_S1 _{ }

S2 ( k  i)  str2num

^S2 k  i^

max

1

Y

 1_k if

 S11  Y


k
1  max

1

 S11

k i k i
S3  str2num_S3 _

2_k  ^

k i

k i

_{  } _j

_k _^T _ _j

_k _

Рис.4. Перевод текстовых файлов в

max

2

Y

 2_k if

 S21  Y


k
2  max

2



 S21

цифровые.

4. 
   Подготовим «неизвестные»
   

спектры. На самом деле спектры, кото-

31 ^{k }T^Y ^j  S31 ^k

   
 max

1

j

Y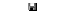
_{3k } X 

рые мы называем «неизвестными» нам

max

3

k

  ^{  }  S

 3_k if 3_k
C:\Ìîè äî

3

^  известны. Первый из этих спектров при- надлежит бензину А-76, второй – бензи- ну АИ-95, третий – бензину АИ-98. Мы должны проверить, правильно ли распо-

MAX _j  0

знает их формируемая нами программа. Введем «неизвестные» спектры,

for


for

i  1 3


j
MAX  max

i

i

i  1 3
if MAX _j
 max

i

как мы это делали для известных спек- тров, дав им имена X₁, X₂, X₃,выделим третьи столбцы и переведем их в циф- ровую форму ( см. рис.5).

K_j  i

if MAX max


j
i

X  X 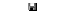

2 3

i

K_j  "76"
if K_j 1

C:\Ìîè äîê

C:\Ìîè äîê

K  "95"

if K 2


X 

_j _{ X }₃

j

K  "98"

j

if K 3


₁ Y

Y  str2num_Y _

j j _ "76" _

j K  ^ "95"

C:\Ìîè äî



k j

k j



K _ "98" _

тров

Рис.5. ввод «неизвестных» спек-

4. 
   Составим программу поиска максимального значения меры сходства каждого «неиз-
   

вестного» со всеми известными спектрами .

4. 
   Так как у нас три «неизвестных» спектра, то мы организуем цикл по j от 1 до 3.
   

Переменными max₁,max₂,max₃ мы обозначим максимальные значения мер сходства со спектрами бензинов А-76, АИ-95 и АИ-98, соответственно. В начале мы присвоим им нуле- вые значения .

9. 
   В каждой марке бензинов мы имеем четыре известных спектра. Поэтому организу- ем цикл по «к» от 1 до 4-х. В этом цикле мы ищем максимальные значения меры сходства каждого из «неизвестных» спектров и спектрами каждой марки.
   
10. 
    Эти вычисленные максимальные значения циклом по «i» мы помещаем в вектор
    

MAX.

9. 
   Следующим циклом по «i» мы помещаем в вектор «К» условный номер марки бен- зина. Группа 1 – бензин А-76, группа 2 – бензин АИ-95, группа 3 – бензин АИ-98.
   
10. 
    Наконец, для большей наглядности присваиваем группе 1 имя «76», а остальным, соответственно, имена «95», «98».
    
11. 
    Слева приведен вектор ответа. Видим, что распознавание произведено правильно.
    

ЛАБОРАТОРНАЯ РАБОТА № 15. НЕЙРОННЫЕ СЕТИ. ПЕРСЕПТРОН.

Искусственный нейрон.

Искусственный нейрон (рис.1) имитирует в первом приближении свойства биологиче- ского нейрона.

На вход искусственного нейрона поступает некоторое множество сигналов, каждый из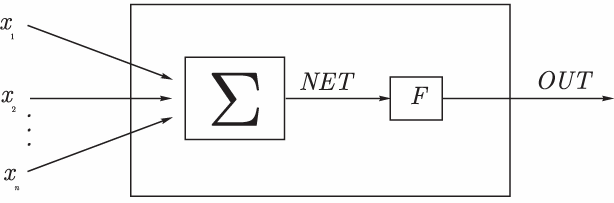

которых является выходом другого нейро- на. Каждый вход умножается на соответ- ствующий вес, и все произведения сумми- руются, определяя уровень активации нейрона.

Рис.1 Модель искусственного нейрона
Множество входных сигналов, обозначенных x₁,x₂,…x_n, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаются вектором X, Каждый сигнал умножается на соответствующий вес w₁,w₂,…w_n, и поступает на суммирующий блок, обо- значенный Σ. Множество весов в совокупности обозначается вектором W. Суммирующий блок, складывает взвешенные входы алгебраически, создавая выход, который мы будем на- зывать . В векторных обозначениях это может быть компактно записано следующим образом:

NET=XW
Сигнал NET далее, как правило, преобра-

зуется функцией активации F и дает выходной нейронный сигнал OUT. Возможны совер- шенно различные функции активации. Но чаще всего используются (см. рис.2):

1. 
   обычная линейная функция OUT=k(NET), где k— константа, величина которой ме- няет наклон функции.
   
2. 
   пороговая функция, где k- величина порога, изменение которой сдвигает порог,
   

3. 
   логистическая функция
   

OUT=

1


1+exp(k NET)

На рис.2 приведены основные активизационные функции нейронов и способы их фор- мирования в Маткаде.

ORIGIN  100
k1  10

i  30  30

 _i  1.5i

k2  0.9
k3  0.1

a3_i  ¹

^a1_i ^{ if}^ _i ^{ k1  0  1}

a2_i  (k2  )_i

^{1  exp}^{k3 } _i

a1 _i
 60  40  20
0 20 40 60

 _i
a2 _i



60
40
20
60  40  20
 20
 40

^{60 a3}i


 _i

 60  40  20


0 20 40 60

 _i

Рис.2. Основные функции активации и их реализация в Мат- каде.
Так как наши графики захватывают третий и четвертый квадранты, то счет мы начина- ем от -100 (ORIGIN:= -100).

Логистическая функция используется наиболее часто, т. к. она обладает свойством дифференцируемости, что нужно при обучении нейрона, и имеет переменный коэффициент усиления: при малых значениях аргумента он большой, а при увеличении аргумента – уменьшается. Изменение коэффициента k изменяет крутизну логистической функции.
Задание1. Студент сначала должен разобраться в приведенных выражениях, а затем набрать каждую функцию в Маткаде по очереди

А). Для пороговой функции следует рассмотреть ее работу при значениях порога к1= 0

и +15.

Б). Работу линейной функции следует проверить при значениях коэффициента к2= 5 и -

1;

В). Вид логистической активизационной функции нужно рассмотреть при значениях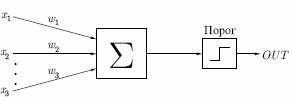

коэффициента к3 = 0.1, 1.5 и 3.
Персептрон.

Нейрон или нейронная сеть, с пороговыми функциями активации называется персептроном. ( Рис.3). Это одна из самых простых нейронных моделей. Она разработана в 60-х гг. прошлого ве- ка Розенблаттом.

Рис.3 Персептрон на три входа.

На входы персептрона подаются входные сигналы. Элемент 

умножает каждый вход на вес и суммирует взвешенные вхо-

ды. Если полученная сумма больше заданного порогового значения, выход равен единице, в противном случае - нулю.

А). Обучение персептрона. Персептрон способен к обучению. Сеть обучается, чтобы для некоторого множества входов давать желаемое множество выходов. Каждое такое вход- ное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно стано- вятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.

Различают алгоритмы обучения с учителем и без учителя. Обучение с учителем пред- полагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с по- мощью обратной связи подается в сеть, и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются по- следовательно, ошибки вычисляются и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.

Персептрон может быть обучен не всему. Некоторым функциям, например, исклю- чающему ИЛИ, его обучить нельзя. Функции, которым можно обучить персептрон, называ- ются линейно разделимыми. Их определение составляет нетривиальную задачу. В этом огра- ниченность персептрона.

Предложенный Ф. Розенблаттом метод обучения состоит в итерационной подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах. Алгоритм включает несколько шагов:

Шаг0: Для заданных входов задается желаемый выход. Начальные значения весов всех нейронов представляются случайными.

Шаг1: Вычисляется вектор ошибки δ между заданным и полученным значением выхо-

да.

T


i

i
Шаг2: Вектор весов модифицируется по формуле ^Wi+1 ^=W+ηXδ . Здесь W и W_i+1 –

Векторы весов до и после очередной итерации, Х- вектор входных сигналов, δ^Т- транспони- рованный вектор ошибки, 1<η<1 – темп обучения.

Шаг3: Шаги 1 -2 повторяются до тех пор, пока вектор ошибки не станет достаточно ма-

лым.

На рис.4 приведена Маткад- программа обучения персептрона из одного нейрона с

двумя входами.

1. 
   Задаются порог к, случайные значения входов х01 и х02, желаемое зна- чение выхода у0=1 и нулевые начальные значения весов w.
   
2. 
   Составляется программа обучения. Задается начальное значение ошибки D=2 и в цикле с оператором while D>0 подсчитываются сумма Σ, фактическое зна- чение и выхода у.
   
3. 
   Подсчитывается ошибка D = y0 – y и новое значение весов с коэффици- ентом обучения η =1.
   
4. 
   Цикл продолжается пока D>0. В результате получаем значение вектора
   

W 

D  2 while D  0

  w₁x01  w₂x02

W, удовлетворяющее требуемой величине ошиб- ки.

ORIGIN  1

y  0

if   k
  1

y0  1
i 

^kwi^100 1  2

y  1

otherwise

D  y0  y

w₁  w₁  Dx01

 ⁰ 

w 

 ⁰ 
x01  rnd (5)

w₂  w₂  Dx02 D

W  w

_ 6.292 _

W 

_ 3.094 _

x02  rnd (1)

x02  0.773

x01  1.573

Рис.4 Программа обучения персептрона.
Убедимся, что при полученных значениях весов, выход персептрона равен 1.Для этого составим небольшую программу, приведенную на рис.5.

y 

  W₁x01  W₂x02

y  0 if   k

y  1 y

otherwise
y  1

Рис.5.Проверка вычисленных весов. Из программы видно, что при подаче заданных входных сигналов выход равен 1.

Б).Обученный персептрон разделяет входные сигналы на два класса.

Если на вход персептрона подать входные сигналы, то , в зависимости от знака Σ выход будет равен 0 или 1. Тем самым входные сигналы делятся на два класса. Так как в векторной форме ^Σ=XWT, то выражение Σ=0 является границей этих двух классов.

На рис. 6 приведена программа классификации десяти точек. Случайным образом сформированы десять входных сигналов. Для подсчитанных выше весов из условия Σ=0 граница. Все входные сигналы располагаются выше или ниже этой границы в зависисти от того, равен соответствующий им выход един единице или нулю.

j  1  10

X1  10  10

W₁

X2(X1)  X1

W₂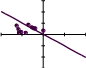
30

20

X2(X1) ¹⁰

x1_j  rnd (9)


x2_j  rnd (9)

x2_j

 10

 5 _{ 10} 0 5 10

 20

 30
X1 x1_j

Рис.7. Разделение входных сигналов персептрона на два класса

ЗАДАНИЕ 2. Студент должен разобраться в программах, набрать их в Маткаде и про- играть их несколько раз.
ЛАБОРАТОРНАЯ РАБОТА № 16. ОБУЧЕНИЕ ОДНОСЛОЙНЫХ НЕЙРОННЫХ СЕТЕЙ.

Обучение с учителем заключается в том, что на вход сети подаются определенные сиг- налы, а веса подстраиваются так, чтобы выход соответствовал заданному значению.

Обучение однослойных сетей.

Однослойной называется сеть, состоящая из одного слоя нейронов (см. рис.1).Здесь каждый входной сигнал р _i подается с весом w _i на входы сумматора данного разряда Σ _i.С выходов сумматоров сигналы поступают на не показанные на рисунке активизационные функции Fi..Обучение таких сетей можно проводить, методом наименьших квадратов, ми- нимизируя квадрат ошибки – разности между реальным и заданным результатом. На рис. 2 показано такое обучение в Маткаде .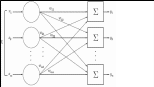

Рис. 1 Однослойная нейронная сеть.

Рассматривается однослойная нейронная сеть, состоящая из «m» нейронов с логистиче- ской функцией активации.

Конкретно в данной задаче принято m=10.

ORIGIN 1

m  10

i  1 m

j  1 m

p_i  rnd (1)

t_i  rnd (1)

	1
1	0.989
2	0.119
3	8.923·10-3
4	0.532
5	0.602
6	0.166
7	0.451
8	0.057
9	0.783
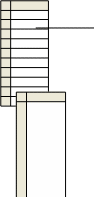10	0.52

1

1_m 1.268·10^-3

Given

2



2
_{ ti}

3 <sub>

</sub>0.193 0.585

1 _{ 0}

^ _i^{T }

_{p } t 

i₄ 1 _

5

6

7

8

9

1	2.217·10-3
2	0.193
3	0.585
4	0.35
5	0.823
6	0.174
7	0.711
8	0.304
9	0.092
10	0.147

10

3. 
   ₅ exp_w
   

0.823

w⁰^.¹⁷M⁴ inerr(w)

0.71

0.304

0.091


0.147
1

p_{ }

_i 

_i



4



10
max(t)^{T }

_i  t_i  T_i

max^^  1.222

Рис.2. Обучение однослойной сети.
Здесь:

1. 
   Командой ORIGIN:=1 объявляется начало счета ;
   
2. 
   Вводится число нейронов в сети (m:=10).
   
3. 
   Начальные значения весов задаются равными 0 (w_i,j :=0);
   
4. 
   Значения входных сигналов p_i и выходных сигналов t_i задаются случайным образом функцией rnd(1). Как известно, эта функция реализует равномерно распределенное число в пределах 0- число в скобках. Так как в скобках стоит единица, то все значения этих функций будут расположены в пределах 0 – 1. Значения выбранных входных и выходных сигналов показаны в виде векторов p и t.
   
5. 
   Далее набирается заголовок решающего блока Given и выдвигается требование, ра- венства нулю суммы квадратов разностей между желаемым выходным сигналом t_i и реаль-
   

ным входным сигналом. Реальный входной сигнал формируется логистической активизаци- онной функцией

1

_{1 } ^{ } _ _i _^{T }

exp__ w p _

Здесь i-ый столбец матрицы весов.

_i

w
Произведение этого транспонированного

столбца на вектор входных сигналов дает сумму произведений соответствующего веса на входной сигнал.

6. 
   совместное написание команд
   

1  ^
m _ 1 _²

А) ^

i  1

_t_i 

_

 

exp__

_i _^T

^ 0




w
^p

и Б)

w  Minerr( w)
требует подобрать веса

_i