методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
(Стохастическое динамическое программирование). Стохастические задачи. Типичным для задач управления является случай, когда имеющаяся информация бывает или недостаточна для точной оценки ситуации, или искаже- на посторонними факторами. Тем не менее, недостаточность информации не снимает задачи принятия решения. Особенность задач управления именно в том и состоит, что решение должно быть обязательно принято независимо от того, в состоянии ли мы точно оценить ре- зультаты, к которым приведет принятое решение. Таким образом, в процессе управления возникает важная задача принятия решения в условиях, когда информация о сложившейся ситуации или недостаточна, или искажена. Данная задача получила название задачи приня-тиярешения вусловияхнеопределенности. Метод динамического программирования позволяет решать вероятностные задачи. Задача 1.Завод выпускает продукцию. Он может находиться в двух состояниях: спрос на продукцию есть; спроса на продукцию нет. Работой завода можно управлять с помощью двух стратегий: стратегия 1 – не тратиться на рекламу и научные исследования; стратегия 2 – тратиться на них. Для каждой стратегии задана своя стохастическая матрица ( матрица вероятностей пе- рехода из одного состояния в другое и своя матрица доходов. 0.5 P1 0.5 9 3 0.8 0.2 4 4 0.4 0.6 R1 3 7 P2 0.7 0.3 R2 1 19 Здесь P1, P2 – матрицы вероятностей переходов завода из одного состояния в другое. Например, P111 – вероятность того, что завод, находящийся в состоянии 1 останется в этом состоянии, P112 – вероятность того, что завод, находящийся в состоянии 1 перейдет в со- стояние 2, P1 22 – вероятность того, что завод, находящийся в состоянии 2 останется в этом состоянии и P121 - вероятность того, что завод, находящийся в состоянии 2 , перейдет в сосо- тяние1. Таковы же элементы матрицы P2. В матрице R1 элемент R111 – ожидаемый доход от деятельности завода, если он оста- нется в состоянии1, R112 – ожидаемый доход завода при переходе из состояния 1 в состоя- ние 2, R122 - ожидаемый доход ( убыток,т.к. доход отрицателен) завода, остающегося в со- стоянии 2, R121 – ожидаемый доход завода при перходе из состояния 2 в состояние 1. Таков же смысл элементов матрицы R2. Задача состоит в том, чтобы, в каком бы состоянии завод не находился, выбрать стра- тегию ( управление) ,приносящую максимальный ожидаемый доход. Перед нами вероятностная задача: управление (выбор стратегии) изменяет вероятность перехода из одного состояния в другое. Переход происходит дискретно, т.е. это дискретный случайный процесс. При выборе стратегии вероятность перехода из одного состояния в дру- гое зависит только от состояния в настоящий момент времени. Следовательно, этот случай- ный процесс является Марковским. Ожидаемый доход – это сумма вероятностей получения того или иного дохода. Рассмотрим первый шаг управления работой завода – первый выбор стратегии. Обо- значим через F ожидаемый доход. Если завод находится в состоянии 1, то он может остать- ся в этом состоянии или перейти в состояние 2. При этом может быть использована как стратегия 1, так и стратегия 2. В первом случае F11 - ожидаемый доход при состоянии 1 и выборе стратегии 1 составляет: F11 =P111 R111 +P112 R112. После подстановки чисел получим: F11= 6. Аналогично, при выборе стратегии 2 ожидаемый доход будет составлять F12= P211R211+P212R212=4. Однако завод может находиться в состоянии 2 и для управления также может быть вы- брана одна из стратегий. В этом случае F21=P122R122+P121R121= -3 при выборе первой стратегии и F22=P222R222+P221R221= -5 при выборе второй стратегии. Эти расчеты можно сделать выбором на первом шаге управле- ния. Для получения максимального ожидаемого дохода следует выбрать стратегию 1 ( не использовать научные исследования и рекламу) , в каком бы состоянии завод не находился. На каждом следующем шаге «n » управления мы должны выбирать управление так, чтобы получить максимальный ожидаемый доход за все «n» шагов. Обозначим макси- мальный ожидаемый доход за первый шаг при нахождении завода в состоянии 1 через f1, а при нахождении завода в состоянии 2 через f2. Из предыдущих расчетов следует, что f1=6 и f2=-3. На втором шаге управления ожидаемый доход с учетом максимального ожидаемого дохода на первом шаге составит при нахождении завода в состоянии 1 и выборе стратегии1 F11= P122(R122+ f1) + P112 (R112+f2) =0,5(9+6) + 0,5 (3-3) =7,5 или F12=P211(R211+f1) +P212 (R212+f2)=0,8(4+6) +0,2( 4-3) =8,2 при выборе стратегии 2.Очевидно, что при нахождении завода в состоянии 1 следует для получения максимального ожидаемого дохода выбирать стратегию 2, т. к. f1=8,2. При нахождении завода в состоянии два, проведя аналогичные расчеты получим F21=P1 22 (R122+f2) +P121(R121+f1) =-2,4 при выборе первой стратегии и F22=P222(R222+f2) +P221(R221+f1)= -1,7 при выборе второй стратегии. Очевидно, что в обоих случаях для полу- чения максимального ожидаемого дохода нужно выбирать стратегию 2. ORIGIN 1 Подобным образом рассчи- тывается оптимальное управление P1 0.5 0.5 R1 9 3 P2 0.8 0.2 R2 4 4 и на всех последующих шагах. 0.4 0.6 3 7 0.7 0.3 1 19 Ниже представлена програм- ма в Маткаде для решения данной u  f f for 0 0 i 1 n n 2 задачи. Запись ORIGIN=1 означает, что счет начинается не с нуля, а с единицы. Далее приводятся матрицы перехода и матрицы доходов для двух стратегий. В самой про- грамме вычисляются доходы Fi,j для всех  F P1 F P1R1 f P1 R1 f четырех возможных случаев и выбирается 1 1 1 1 1 1 1 1 2 1 2 2 управление «u» в зависимости от того, ка- F P2 R2 f P2 R2 f 1 2 1 1 1 1 1 1 2 1 2 2 кие доходы больше. Принято U=1 для пер- F P1 R1 f P1 R1 f вой и U=2 для второй стратегии. После это- 2 1 2 2 2 2 2 2 1 2 1 1 го формируется вектор «max» для каждого F P2 R2 f P2 R2 f случая. Программа набрана для случая вы- 2 2 2 2 2 2 2 2 1 2 1 1 i i i i u1 1 u1 2 u2 1 u2 2 if F F 1 1 1 2 otherwise if F F 2 1 2 2 otherwise числения «u» и приведены его значения для двух шагов управления. ЗАДАНИЕ: 1. Набрать программу. 2. Вычислить значения векторов «u», «max», двух, пяти и 10 шагов управления. max F if F F 1 i 1 1 1 1 1 2 max F otherwise 1 i 1 2 max F if F F 2 i 2 1 2 1 2 2 max F otherwise 2 i 2 2 1 i f1 f1 max 2 i f2 f2 max i u u 1 2 1 2 ЛАБОРАТОРНАЯ РАБОТА №8. ОЦЕНКА КАЧЕСТВА ПИЩЕВЫХ ПРОДУКТОВ.(Оценка качества пищевых продуктов методами регрессионного анали- за). Задача 1. Оценка качества томатов. В качестве объективного показателя при оценке качества томатов выбрали оптическую плотность при длине волны =360 нм (). Установлена экспериментальная зависимость 10- балльной органолептической оценки (y) от оптической плотности (x):
Для решения задачи объективной оценки качества томатов используем линейную регрессию. В Маткаде, как уже говорилось выше, коэффициенты линейной регрессионной зависимости определяются с помощью встроенных функций slope ( наклон) и intercept (от- резок, отсекаемый на координатной оси)  ORIGIN 1 ORIGIN 1 5 0.98 4.5 1.1 1.25 3.5 3.0 1.39 0.99 5.0 4.5 vx 1.14 intercept(vx vy) 9.59 vy 1.28 3.5 slope(vx vy) 4.644 3.0 1.43 1.1 4.5 4.0 1.22 3.5 3.0 1.45 Рис.1. Исходные данные и вычисление коэффициентов регрессии. На рис. 1 приведены вектора исходных данных – вектор vy- органолептической оценки качества томатов и вектор vx- оптической плотности томатов. Здесь же показано применение встроенных функций вычисления коэффициентов прямой и уравнение линейной регрессии, использующее эти коэффициенты. На рис.2 точками показана органолептическая оценка и сплошной линией – аппрокси- мирующая ее прямая. Здесь же показаны максимальные ошибки оценки в баллах (она равна 0,204 балла) и в процентах ( 4,083 %). x 0.9 1.9 j 1 12 6 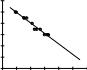 5 5y(x) 4  max 0.204 max 4.083 3 vyj    2 21 0.8 1 1.2 1.4 1.6 1.8 2 x vxj Рис.2 График оценки качества томатов. Задача 2. Инструментальная оценка качества шампанского Сегодня существенная часть шампанских вин в России и в мире производится непре- рывным способом. Этот способ был разработан в СССР еще в 60-х годах, и авторы разра- ботки Г.Г. Агабальянц, А.А. Мержаниан и С.А. Брусиловский были награждены Ленинской премией. При таком способе производства обычный выборочный органолептический кон- троль недостаточен. Поэтому задача инструментальной оценки качества шампанских вин является вполне своевременной. Описанная ниже инструментальная оценка качества шампанского разрабатывалась по статистическим данным, приведенным в (С.П. Авакянц. Биохимические основы технологии шампанского. М., «Пищевая промышленность»1980). В этой книге приведены экспертные балльные оценки и состав, а также физико- химические, окислительно-восстановительные, биохимические показатели и показатели бу- кетистых веществ (всего 35 показателей) для 59 образцов Советского шампанского. На основе этих показателей была построена теоретическая балльная оценка, которая сравнивалась с экспертной. Задача решалась методом наименьших квадратов в пакете Маткад .Решение проводи- лось в решающем блоке GIVEN с использованием встроенной функции MINERR. Первоначально была проведена проверка экспериментального материала на выбросы. Оказалось, что весь этот материал статистически достоверен. Затем были вычислены парные коэффициенты корреляции межу всеми показателями и парные коэффициенты корреляции показателей с органолептической балльной оценкой. В результате для дальнейшего исследования оставлено только следующие восемь показателей с максимальными коэффициентами парной корреляции и максимальными коэффициентами корреляции с балльной оценкой: Содержание этанола % объема Титруемая кислотность г/л. Летучие кислоты г/л, Содержание ионов железа мг/л, Устойчивость двусторонних пленок с., Оптическая плотность при длине волны λ=280нм., Доминирующая длина волны нм., Свободные альдегиды мг/л.
На рис.3.показана часть сформированной из этих показателей таблицы М2.  M2 M2 Рис.3. Таблица исходных данных. Здесь первый столбец – балльная оценка, а остальные столбцы – значения перечислен- ных выше показателей. Таблица имеет 59 строк и девять столбцов. Весь отобранный экспериментальный материал был разделен на обучающую и кон- трольную части. Обучающая последовательность использовалась для определения параметров аппрок- симирующей функции, на контрольной части оценивалась точность оценки качества по этой функции. Для контрольной части были отведены 10 опытов из 59. Номера экспериментов кон- трольной части для большей объективности выбирались случайным образом, т. е. они об- новлялись при каждом новом решении. Соответственно, рассчитанные параметры и резуль- таты каждого решения несколько отличались один от другого. На рис.4.показаны операторы и номера строк случайного выбора контрольных экс- периментов. i 1 10 ui 1 floor(rnd(59)) uT
Рис 4. Результат случайного выбора десяти контрольных экспериментов.
С помощью вспомогательной программы контрольные эксперименты были исключены из исходных данных, в результате чего получена показанная на рис.5 таблица М3 опор- ных значений показателей, по которым и определялась аппроксимирующая гиперпло- скость. M3 Рис.5. Таблица опорных значений показателей После разделения экспериментального материала на обучающую и контрольную части, на основании значений этих показателей и приведенных экспертных балльных оценок ме- тодом наименьших квадратов была построена статистическая функциональная зависимость теоретической балльной оценки от этих показателей. Как известно, выбор вида аппрокси- мирующей функции в методе наименьших квадратов сам по себе является сложной задачей. В данной работе аппроксимация производилась наиболее простой -линейной функцией вида ball=a1+aj Xj j=2 (1) где ball – оценка в баллах , Xj-значение j-ого выбранного показателя ; aj - коэффици- енты показателей, значения которых и определяются методом наименьших квадратов.На рис.6. приведено решение задачи в Маткаде в решающем блоке Given. j 1 9 aj 1 49 9 Given 2 a1 a M3 M3 0  a Minerr(a) i 1 j i j j 2 i 1 aT 0.25 0.508 0.238 0.494 0.072 0.024 0.251 1.305 3 7.018 4 10 10 Рис.6. Определение коэффициентов методом наименьших квадратов. Сначала задаем начальные приближения для искомых коэффициентов aj. Их всего де- вять. Затем в блоке given набирается сумма сорока девяти ( по количеству строк в таблице М3) квадратов разностей инструментальной оценки (1) и органолептической балльной оцен- ки в первом столбце таблицы М3. Записывается требование равенства нулю этого выраже- ния. Но так как выдержать это требование невозможно, ниже записывается требование опре- делить вектор коэффициентов «а» с минимальной ошибкой (minerr).Задача решается и ниже приведено ее решение – значения элементов матрицы коэффициентов а. Подобрав коэффициенты «а» мы определили девятимерную линейную функцию, ап- проксимирующую зависимость балльной оценки качества шампанского в зависимости от значений объективных показателей. Теперь следует проверить, насколько точно проводится эта аппроксимация. Сначала проведем эту проверку для опорных значений показателей, а затем для кон- трольных значений. Результаты проверки относительно опорных значений показателей при- ведены на рис.7,а результаты проверки относительно контрольных показателей - на рис8. i . 1 49 vi M2 9 a 1 a M2 j i 1 j j 2 i
vT max(v) 0.514
wT min(v) 0.543 w i v 100 i 1 max(W) 0.717 max( w) 5.308 min(w) 5.222 Рис.7.проверка точности аппроксимации для опорных значений показателей. На рис.7 сначала приведена формула для подсчета абсолютной ошибки v в баллах, где М2- матрица опорных значений показателей, ниже — вектор значений абсолютных ошибок(для экономии места в транспонированном виде), максимальные ошибки в баллах. Ниже приведена формула для расчета относительной ошибки w в процентах, а также ее максимальное значение. Максимальная ошибка в баллах равна 0,543, а максимальная ошибка в процентах -5,308%. На рис.8 сначала в транспонированном виде приведен вектор номеров контрольных опытов u, затем приведена формула для расчета инструментальной балльной оценки и фор- мула подсчета абсолютной ошибки W. Ниже приведены значения абслютных ошибок, а так- же их максимальная и минимальная величины. Затем на рисунке приводится выражение для относительной ошибки в процентах и максимальное и минимальное значение этих ошибок. Мы видим, что максимальная ошибка инструментальной балльной оценки контроль- ных параметров не превышает 0,717 балла, а относительная ошибка не превышает 7,836%. max(w) 7.836 Проверка показала, что сформированная математическая модель позволяет достаточно точно определять балльность шампанского по измеренным значениям следующих показате- лей: Содержанию этанола % объема, Титруемой кислотности г/л., Летучим кислотам г/л, Содержанию ионов железа мг/л, Устойчивости двусторонних пленок с., Оптиче- ской плотности при длине волны λ=280нм., Доминирующей длины волны нм., Свободным альдегидам мг/л.  balli a2M2ui 2 a3M2ui 3 a4M2ui 4 a5M2ui 5 a6M2ui 6 a7M2ui 7 a1 Wi balli M2ui 1 balli a2M2ui 2 a3M2ui 3 a4M2ui 4 a5M2ui 5 a6M2ui 6 a7M2ui 7 a1 Wi balli M2ui 1
T T W u min(W) 0.436 Максимальная и минимальная ошибки в процентах |
