методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов

• Название: Методические указания для проведе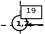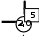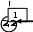ния лабораторных работ по дисциплине Моделирование систем и процессов
• Анкор: методические указания
• Дата: 19.09.2022
• Размер: 1.02 Mb.
• Имя файла: методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1.docx
• Тип: Методические указания; #685529
• страница: 8 из 19

4 6 ₈

6 6 7 4

₃ 7 8

^{2 5 6} 1

₇ 3 5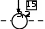

4 ² 8 2

₅ 6 4

Рис. 1.

динамического программирования имеет вид:

справа налево (управление ) или по вертикали снизу вверх (управление u₂). На рисунке задана цена перехода из одного узла в другой. Нужно выбрать такой путь, чтобы суммарная цена была минимальной. Внутри окружностей заданы координаты каждого узла. Как бы мы ни двигались, решение задачи требует шести шагов. Будем решать задачу « наоборот», двигаясь из точки В с координатами (0,0) в точку А с координатами (3,3). В этом случае возможно движение только вниз или справа налево.

Рекуррентная формула для решения задачи методом

k
f(x)=^min [Q(x,u)+f

u
k1

(x^')]

Будем действовать в соответствии с этой формулой (рис.1). Рассмотрим переход в каж- дую точку нашей системы и, если возможны варианты переходов, выберем тот переход, для которого общая сумма потерь является наименьшей. Начинаем движение из точки (0,0). В этой точке еще никаких потерь нет, поэтому ставим в прямоугольник около узла число 0. В т.(1,0) можно перейти только из т.(0,0) с платой 4 единицы. Рисуем стрелку и ставим около узла число 4. В т. (2,0) можно перейти только из т.(1,0) с общими потерями 4+1=5. Рисуем стрелку и ставим это число около узла. Аналогично проводим стрелки и заполняем узлы (3,0), (0,1),(0,2) и (0,3). После этого рассмотрим переход в т. (1,1). В нее можно перейти из т. (1,0), при общих потерях 4+8 =12, и из т. (0,1) с общими потерями 8+7 =15. Выбираем пер- вый путь, проводим стрелку и ставим около узла число 12. В т. (1,2) можно перейти из т. (0,2) или из т.((1,1). Выбираем второй путь, так как при нем общие потери 12+7=19 меньше. Аналогичным образом просчитываем и выбираем переходы ко всем остальным точкам. В результате оказывается, что существует только один путь к т. (3,3). Он то и является опти- мальным. На рис.1 он выделен жирными стрелками.

До построения собственно программы задаем координаты начальной и конечной точек, объявляем о начале отсчета с 1 (ORIGIN:=1), задаем значения коэффициентов a,b

и

ORIGIN  1
x0  2

x1  12


y0  2

y1  12

выбираем шаг d (см. рис. 2).

Рис.2

a  5
b  30
d 

y1  y0 1000

V 

S  0 x  x0
Сама программа приведена на рис.3.

y  y0
[( x1  x0) 
( y1
 y0 )]

В доцикловой части программы задаем начальные значения перемен-

for

i  1 

d

ным x,y и функции S.

В начале цикла в операторе for

u  2
u  1

if ^S 

if ^S 

2
a  x  S 

2

2
a  x  S 

b  y^ 

b  y^ 
( y  y1 )
( x  x1)

определяем количество точек. Мы проведем вычисления для четырех точек. Соответственно, j=0 ..3 Оче- видно, что каким путем мы бы не

S  S  a  x S  S  b  y

if u 1 otherwise

шли, нам придется пройти (x1-x0)/d

точек по горизонтали и (y1-y0)/d то- чек по вертикали, т. е. всего [(x1-

x  x  d

y  y  d

if u 1

if u 2

x0)+(y1-y0)]/d точек.

Далее в цикловой точке мы,

V

V

V
i  1 ^{ x} i  2 ^{ y} i  3 ^{ u}


1
V _{ 4}  S V  i

прежде всего, выбираем управление, минимизируя полную цену. Полная цена всего движения для данного уча- стка состоит из цены движения на всех предыдущих этапах S и прира- щения цены при движении на данном участке. При движении по горизонта- ли это приращение равно ax ², при

1  6

V

движении по вертикали – by.

Рис.3. Программа выбора оптимальной траектории

Но так как движение системы не должно выходить за пределы квадрата x1-x0, y1- y0, то одновременно при выборе управления мы проверяем нахождение системы в этом квадрате. Для возможности движения по вертикали должно выполняться условие

y ≤ y1, а для возможности движения по горизонтали – условие x ≤ x1. Выбрав управление, мы подсчитываем новое значение полной цены S и определяем новые значе-

ния координат x и y.

13

12.267

11.533

10.8

10.067

9.333

8.6

_{Vj  2} 7.867

7.133

6.4

5.667

4.933

4.2

3.467

2.733

2

Для сохранения в памяти и вывода на пе- чать вводим новые значения в столбцы матри- цы V. Программа составлена.

На рис.4 представлен график решения за-

дачи.

22.636.733344.656.733366.676.733388.696.73331100.1616.733132

^Vj  1

Рис.4. График оптимальной траектории.

ЛАБОРАТОРНАЯ РАБОТА №6.ОПТИМАЛЬНОЕ СОЗРЕВАНИЕ

СЫРОКОПЧЕНОЙ КОЛБАСЫ (Динамическое программирование).

Рассмотрим задачу оптимального управления созреванием сырокопченых колбас. Процесс производства сырокопченых колбас состоит в составлении фарша из исходно-

го сырья ( говядины высшего сорта, полужирной свинины, шпика), который затем шприцу- ется в оболочку, и полученные батоны колбасы помещаются в камеру созревания.

. В процессе созревания происходят распад белков, накопление ароматобразующих ве- ществ и другие биохимические реакции. Все эти превращения приводят к накоплению мо- лочной кислоты в колбасе, что ведет к изменению показателя его кислотности рН.

С целью сокращения созревания сырокопченых колбас в них при составлении фарша вносятся стартовые культуры. Стартовые культуры способствуют подавлению жизнедея- тельности патогенной микрофлоры за счет деятельности молочнокислых бактерий.

Управлять процессом созревания сырокопченых колбас можно, варьируя управляющие величины: количество и состав стартовых культур, температуру t ◦ С и влажность воздуха ψ

% в камере созревания. Эти же величины являются и контрольными, так как их можно на- блюдать. Управляемой величиной является показатель кислотности pH.

Результаты экспериментальных исследований показали, что процесс созревания зани- мает 21 день и его можно расчленить на восемь шагов, в результате каждого из которых достигается определенные значения показателя кислотности полуфабриката.

1. 
   ый шаг — начальный этап (составление фарша) и первый день созревания, рН₁
   

=(5,60+5,80);

2. 
   ой шаг — второй день созревания, pН₂ = (5,50 +5,70); 3-ий шаг — третий день созревания, рН₃ = (5,35 +5,5);
   

4-ый шаг—четвертый день созревания, рН₄ = (5,20 +5,40); 5-ый шаг — пятый день созревания, рН₅ =(5,10 +5,30);

6. 
   ой шаг — шестой день созревания, рH ₆ =(4,90+5,10);
   
7. 
   ой шаг—с седьмого по двенадцатый день созревания, рН₇ =(4,80+5,00);
   
8. 
   ой шаг—с девятого/двенадцатого по двадцать первый день созревания, рН₈
   

=(5,30).См таблицу 1.

Здесь t и ψ – практически используемые значения управляющих величин, pH – полу- чаемые при таком управлении значения показателя кислотности, pHmin и pHmax – мини

микрофлоры стартовых культур. В результате шагов 2-6 происходит подавление жиз- недеятельности патогенной микрофлоры, накопление молочной кислоты, что обусловливает сдвиг рН в «кислую» сторону. По существу на первом – шестом шагах выбираются допусти- мые управления, обуславливающие качество готовой продукции. Седьмой шаг приводит значение pH к минимуму. Восьмой шаг поддерживает термовлажностные параметры, необ- ходимые для получения продукта заданного качества с конечным результирующим значени- ем pH=5,3. На последних двух шагах управление не варьируется.

День	0	1	2	3	4	5	6	7	8	9	10	11	12
pH	5.6	5.55	5.5	5.4	5.3	5.2	5.1	5.0	4.9	4.85	4. 8	4.8	4.8
PHmin	5.6	5.6	5.5	5.35	5.2	5.1	4.9	4.8	4.8	4.8	4. 8	4.8	4.8
pHma x	5.8	5.8	5.7	5.5	5.4	5.3	5.1	5.0	5.0	5.0	5. 0	5.0	5.0
t	20	20	20	20	18	15	15	15	15	15	15	15	15
ψ	90	88	86	84	82	80	80	80	80	80	80	80	80
шаги		1	2	3	4	5	6	7

Таблица 1

Про

должение таблицы 1

13	14	15	16	17	18	19	20	21
4.85	4.9	4.95	5.0	5.1	5.2	5.25	5.3	5.3
5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3
5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3
15	15	15	15	15	15	15	15
80	80	80	80	80	80	80	80
8

В качестве математической модели процесса созревания сырокопченой колбасы выбе- рем авторегрессионую зависимость,

pH_i a_i pH_i1  b_i t_i c_i_i
(1)

Анализ таблицы 1 показывает, что коэффициенты « b» и «c» практически постоянны, поэтому примем b=-6*10^-4, а c=0,95*10^-4. Коэффициент «a» несколько более изменяется в процессе созревания колбасы, поэтому для этого коэффициента были приняты зависящие от номера шага Значения, приведенные в таблице 2.

Таблица 2.

Шаг	0	1	2	3	4	5	6	7
день	0	1	2	3	4	5	6	7	8	9	10	11	12
«а»	1	0.99	0.98	0.98	0.98	0.98	0.99	0.99	0.99	0.99	0.99	1	1

Продолжение таблицы 2

8
13	14	15	16	17	18	19	20	21
1.01	1.01	1.01	1.01	1.02	1.02	1.01	1.01	1

Созданную математическую модель необходимо, прежде всего, исследовать на адек- ватность. Для этого вычисленный по ней показатель кислотности сравнивался с показателем из таблицы 1 при значениях управляющих величин из этой же таблицы. Для этого была соз- дана программа в Маткаде, приведенная на рис.1.

PH 

PH

0

for

 PHtr

0

i  1 21

t  ttr_i

  tr_i


10
c  0.95  ^{ 4}

a  a_i

b  6  ^{ 4}

10

PH  a PH  b  t  c  

i i1

i

PH
Рис.1. Программа проверки адекватности системы экспериментальным данным и ошибка модели в %

Результаты расчетов по программе приведены в таблице 3.

Таблица 3

Шаг	0	1	2	3	4	5	6	7
День	0	1	2	3	4	5	6	7	8	9	10	11	12
pH практ	5.6	5.55	5.5	5.4	5.3	5.2	5.1	5.0	4.9	4.85	4.8	4.8	4.8
pH мат	5.6	5.484	5.371	5.313	5.20	5.09	4.99	4.89	4.79	4.74	4.69	4.69	4.69
Ошибка %	0	0.174	1.35	1.61	1.8	1.9	1.0	0.12	0.87	0.87	0.84	0.81	0.74

Продолжение таблицы 3

8
13	14	15	16	17	18	19	20	21
4.74	4.78	4.83	4.87	4.97	5.08	5.12	5.17	5.3
4.837	4.884	4.931	4.979	5.077	5.177	5.228	5.279	5.277
0.74	0.68	0.63	0.59	0.57	0.58	0.59	0.61	0.7

Из таблицы 3 видно, что относительная ошибка не превышает 2%. Таким образом, соз- данная математическая модель хорошо отображает экспериментальные данные.

Мы хотим так изменить управление процессом созревания сырокопченой колбасы, чтобы хотя бы немного улучшить ее качество. Так как по мере созревания кислотность по- луфабриката должна снижаться, то для улучшения качества необходимо уменьшать кислот- ность. Для оценки качества управления процессом будем использовать функциональный критерий - выигрыш J в виде относительного суммарного количества патогенной микрофло- ры, прекратившей свою жизнедеятелъностъ в результате накопления массы молочнокислой микрофлоры, а также количества расщепленных белков и других эссенциальных веществ.

J_t _ pH_k min
Запишем основное рекуррентное

уравнение динамического программирования, используя в качестве функции выигрыша

(2)

J_t= − pH_t
что обусловлено фактом снижения значения рН при увеличении

значения J. Так как на восьмом шаге происходит лишь поддержание параметров, то опти- мизацию необходимо проводить только для первых семи шагов.

Из выбранной функции выигрыша следует, что условную оптимизацию всех шагов возможно проводить, выбирая такие управления, при которых.

Как было _J

стартовых культур, а ^k

_{ max} сказано выше, управлением является количество и состав также температура и влажность в камере созревания. В

качестве множества допустимых управлений технологией было выбрано множество Ωу =

{18°С + 25°С} х {80% + 90%}, образованное путем комбинаций (прямого произведения) возможных значений температур и относительной влажности воздуха в камере созревания. Безусловная оптимизация управления соответствует таким наборам {t _k , ψ_k} управляющих воздействий, при которых оптимальная кривая рН _opt проходит ниже всех используемых на практике технологий, т.е. площадь под кривой рН будет минимальной.

Была составлена программа в Маткаде, которая приведена на рис.6.После ввода на- чальных значений температуры, влажности, показателя кислотности и критерия оптимально-

сти начинается варьирование управляющих па-

pH 

t₀  20

f ₀  90

pH₀  5.6

J₀  5.6

раметров.

В программе управление температурой t

и влажностью f ведется на первых шести шагах

( i= 1…6).

for

i  1  6

pH1_i  a_i  pH_{i 1}  b  18  c  80 J1_i  J_i1  pH_{i 1}

На каждом из этих шагов выбираются пу- тем перебора значения t и f, минимизирующее критерий оптимальности J – сумму значений показателя кислотности на всех предыдущих

for

t1  18  25

шагах.

for

t1 t_i  t1

f1  80  90

pH2_i  a_i  pH_{i 1}  b  t1  cf1 J2_i  J_i1  pH_{i 1}

if J2_i  J1_i

J_i  J2_i

pH_i  pH2_i

otherwise

pH_i  pH1_i J_i  J1_i

f1

Для этого сформированы два вложенных цикла по температуре (t1) и влажности (f1), со- ответственно. Начиная с седьмого дня значе- ния температуры и влажности задаются посто- янными ( t=15 град. C, f=80%).

В результате расчетов получены необхо- димые для оптимального решения значения управляющих параметров, значения критерия оптимальности в случае оптимального и не оп- тимального решений, графики и таблицы зна- чений показателя кислотности для обоих случа- ев ( см. рис.7).

На этом рисунке в части А приведены оп- тимальные значения управляющих параметров

– температуры и влажности. В части Б рисунка приведены значения критерия оптимальности

for


pH

f _i  f1 i

i  7  20 t_i  15

f _i  80

pH_i  a_i pH_{i 1}  b  t_i  cf_i i

для случаев оптимального

Jopt =101.755 и традиционного Jtr=107.35 управлений, а также изменение этого критерия в результате оптимального решения

DJ= 5.21%

. В части В показаны значения показателя кислотности при оптимальном управлении, а в части Г по шагам графики показателя кислот- ности при оптимальном ( крестики) и традици- онном ( кружочки) управлении.

Рис.6. Маткад программа определения оптимальных параметров выдержки сырокопче- ной колбасы методом динамического программирования.

Следует заметить, что во-первых полученное улучшение качества колбасы ( величины показателей кислотности) незначительно, что указывает на хороший профессионализм практиков, и во-вторых оптимальное решение крайне чувствительно к значениям коэффи- циентов используемого разностного уравнения. режима созревания сырокопченой колбасы.

t^T 

А)

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
0	90	90	90	90	90	90	90	80	80	80	80	80	80	80	80	80	80	80	80	80	80

f^T 

Б)

20 20

Jopt  _ pH Jtr  _

^pHtr^T

i
Jopt  101.755

i

i  1
i  0

Jtr  107.35

_{DJ } (Jtr  Jopt

Jtr

DJ  5.212%

В)




	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
0	5.6	5.541	5.427	5.315	5.206	5.098	5.044	4.992	4.941	4.89	4.84	4.838	4.837	4.884	4.931	4.979	5.028	5.127	5.228	5.279	5.33

T

pH

Г)

pH_i

5.6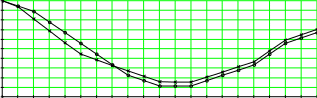

5.51

5.42

5.33

5.24

_pHtrT 5.15

ⁱ 5.06

4.97

4.88

4.79

4.7

0 1 2 3 4

5 6 7

8 9 10 11 12 13 14 15 16 17 18 19 20

i

Р

ис.7. Результаты расчета оптимального режима созревания сырокопченой колбасы.

А)- Необходимые для оптимального процесса значения температуры и влажности по шагам.

Б) Полученная экономия критерия оптимальности DJ= 5,212%.

В) Значения показателя кислотности при оптимальном процессе.

Г) График значений показателя кислотности при оптимальном (крестики) и стандарт- ном ( кружочки ) процессах.

ЛАБОРАТОРНАЯ РАБОТА № 7. ОПТИМИЗАЦИЯ РАБОТЫ ПРЕДПРИЯТИЯ.