методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Задача 3При откорме животных каждое животное ежедневно должно получить не ме- нее 60 ед. питательного вещества А, не менее 50 ед. вещества В и не менее 12 ед. вещества С. Указанные питательные вещества содержат три вида корма. Содержание единиц питатель- ных веществ в 1 кг каждого из видов корма приведено в следующей таблице:
Составить дневной рацион, обеспечивающий получение необхо- димого количества питательных ве- ществ при минимальных денежных затратах, если цена 1 кг корма I вида составляет 9 руб., корма II вида — 12 руб. и корма III вида — 10 руб. Составить математические зависимости и решить задачу самостоятельно. Задача 4.Четыре предприятия данного района для производства продукции используют одно и тоже сырье. Потребности в сырье каждого из предприятий соответственно равны 120,50,190 и 110 единиц. Сырье сосредоточено в трех местах его получения, а запасы соот- ветственно равны 160, 140,170 единиц. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и за- даны матрицей Здесь 7 8  A 4 5 A 4 5 9 3 1 9 9 8 2 6 A1 1 7 A1 2 8 т. д. - цена завоза сырья из пункта 1 в пункт 1; - цена завоза сырья из пункта 1 в пункт 2, и Требуется составить такой план перевозок, при котором об- щая стоимость перевозок является минимальной. Это так называемая транспортная задача. Нарисуем схему возможных маршрутов перевозок: 1 2 3 4 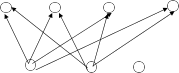 Куда перевозят Куда перевозятОткуда перевозят 1 2 3 Рис.2 Транспортная задача Перевозка из третьего источника сырья на схеме не показана. Обозначим количество груза, перевезенного из пункта 1 в пункт 1 через Х11,
из пункта 1 в пункт 2 через Х12, и т.д. Нам необходимо минимизировать общую стоимость перевозок F. Воспользовавшись матрицей стоимости С, составим уравнение этой стоимости. В общем виде F= а 11Х 11 +а 12 Х 12 + а 13Х 13 + а 14Х 14 + а 21Х 21+а 22Х 22 +а 23Х 23 + +а 24Х 24 + а 31 Х 31+а 32Х 32+а 33Х 33 + а 34Х34 или в цифрах: F=7X 11+8X 12+1X 13+2X 14 +4X 21+5X 22+9X 23+8X 24+9X31+2X 32+ +3X 33+X34 Запасы сырья в каждом пункте отправления и потребности в нем в каждом пункте переработки ограничены. Для первого пункта переработки Х11+Х 21+ Х 31=120. Соответственно, для остальных пунктов переработки имеем: Х12+Х 22+Х 32 = 50, Х 13+ Х 23+ Х 33=190, Х 14+Х 24+Х 34 =110. Для пунктов отправки сырья имеем: Х 11+Х 12+Х 13+Х 14 =160 Х 21+Х 22+Х 23+Х 24= 140 Х 31+Х 32+Х 33+Х 34 =170 Кроме того, так как мы возим сырье только в одну сторону, все переменные должны быть положительными: X 11>0 ,X 12> 0, X 13>0, X 14>0, X 21>0, X 22>0,X 23>0, X 24>0,X31>0, X 32>0,X 33>0,X 34>0. Теперь мы полностью составили уравнения задачи и можем решать ее. Решить задачу в Маткаде. Наберем начальные значения переменных X (по-прежнему равные 1), целевую функ- цию, все ограничения и все числа аналогично задачам 1 и 2. Получим решение. Математическую запись решения можно записать более компактно, используя матричное исчисление. Все переменные задаем в форме матрицы. Заметив, что целевая функция может быть представлена в виде следа ( суммы диагональных элементов) произведения АХТ, где Т – ин- декс транспонирования, записываем ее в такой форме. Все ограничения записываем также сокращенно. Ответ получен в виде матрицы z. И так, следует перевезти из пункта 1 в пункт приема 3 160 единиц груза, из пункта 2 в пункт приема 1 – 120 единиц и в пункт 2 – 20 единиц. Из пункта отправки 3 следует перевезти в пункты приема 2 и 3 по 30 единиц, а в пункт приема 4 – 110 единиц груза. При этом минимальные затраты составят 1000 единиц стоимо- сти. ORIGIN 1 7 A 4 9 8 1 2 5 9 8 2 3 1 1 1 1 1 X 1 1 1 1 1 1 1 1 f(X) trA T X 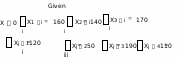 i 1 4 j 1 3 i 1 4 j 1 3 z Minimiz(ef X) 0 0 160 0 f(z) 1000 z 120 20 0 0 0 30 30 110 Рис.3. Решение транспортной задачи в матричной форме ЛАБОРАТОРНАЯ РАБОТА№4.ОПТИМИЗАЦИЯ КАЧЕСТВА МОЛОЧНОЙ КОЛБАСЫ Согласно стандарту вареная молочная и столовая колбасы должны состоять из говяди- ны и свинины Возникла задача добавить в ее состав мясо птицы без ухудшения качества. Сначала были изготовлены модельные колбасы «Молочная высшего сорта» и «Столо- вая первого сорта» без добавления мяса птицы и определены качественные характеристики фарша этих видов колбас. Bсeго было проведено 30 экспериментов (по 3 параллельных опы- та). Результаты эксперимента были подвергнуты математической обработке, полученные чи- словые характеристик приняты за опорные. Опорные (без мяса птицы) безразмерные свойства фарша модельной молочной колба- сы высшего сорта были следующие: Влага - 69,00 ± 1,20; жир - 14,50 ± 1,00; белок-15 +- 0,4, зола- 1,00 ± 0,07; водо - связы- вающая способность – 42, удельное напряжение сдвига - 5700,00 ± 100,00. Введем следующие обозначения массовых долей фарша: М1 содержание говядины 1-го сорта; M 2 содержание свинины полужирной; М3 содержание мяса птицы механической обвалки; М4 - содержание молока сухого цельного; М5- содержание яйца цельного (или крахмала). Тогда условия, при которых фарш с мясом кур механической обвалки максимально приближался к опорному, можно описать в виде следующей системы неравенств: 1) 70,20 77,70 М1 + 66,00 М2 + 70,00 М3 + 4,00 М4 + 74,00 М5 65,00 - содержание влаги; 2)13,50 7,00М1 + 16,00М2 + 16,00М3+25,00М4 + 11,50М5 15,00 - содержание жира; 3) 11,90 20,20 М1 +17,00 М2+13,00 М3+ 26,00 М4+12,70М5 16,10 - содержание белка; 4) 0,93 1,10 М1+ 0,80 М2 + 0,90 М3 + 0,40 М4+ 1,10 М5 1,07 - содержание золы; 5) 30,05 60,00 М1 + 32,50 М2 + 37,00М3 +55,00 М4 +11,00 М5 5 55,00 - показатель во- досвязывающей способности; 6) 5600,00 7000,00 М1 + 6500,00 М2 + 4700,00 М3 + 370,00 М4 +120,00 М5 5800,00 - показатель предельного напряжения сдвига. Для простоты во всех неравенствах введено обозначение М к => М к/100, где к=1 5. При этом получается следующее естественное условие для массовых долей: 7)М1+М2+М3+М4+М5=1. В качестве целевой функции сначала был выбран показатель относите5льной биологи- ческой ценности искомых фаршей. Биологическая ценность характеризует пищевые свойства, вкусовые достоинства, энер- гоемкость и безвредность продукта, служит «надежным индикатором», по которому можно тестировать ту или иную технологию производства животного сырья и продуктов. Однако при моделировании критерий биологической ценности во многих вариантах достигал одного и того же значения 190 – 192. Это говорит о том, что после определенного уровня (190 для данной задачи) этот кри- терий становится менее чувствительным. Иными словами, существовало множество «опти- мальных» решений, которые по критерию биологической ценности практически не отлича- лись. В этих условиях более целесообразным было поддерживать значение этого критерия на достигнутом «квазиоптимальном» уровне, а в качестве различающего критерия выбрать кри- терий себестоимости фарша, который для рассматриваемой модели выглядит так: . СБ =200М1+ 190М2+ 85М3+ 100М4+ 40М5. Здесь 200– цена говядины за 1 кг. , 190 – цена свинины. 85 – цена 1 кг птицы, 100 – це- на молока сухого, 40 – цена яйца. Теперь задачу можно сформулировать так: Найти М1,М2,М3,М4,М5, для которых С.Б достигает минимума при ограничениях 1-7 и дополнительном ограничении на БЦ: . 150.00М1+ 180ю00М2+ 260.00М3+ 100.00М4+ 125М5≥ 190.00 В соответствии с описанными условиями данная задача была решена в Маткаде. Её ре- шение приведено на рис.1 f(M1 M2 M3 M4 M5) 200M1 190M2 85M3 100M4 40M5 М1- количество мяса по цене 200р/кг, М2 - количество свинины по цене 190р/кг М3- количество мяса птицы 85р/кг, М4 - количество сухого молока 100р/кг М5 -количество яиц 40р/десяток M1 1 M2 1 Given M3 1 M4 1 M5 1 M1 0 M2 0 M3 0 M4 0 M5 0 77.7M1 66M2 70M3 4M4 74M5 70.2 77.7M1 66M2 70M3 4M4 74M5 65 7M1 16M2 16M3 25M4 11.5M5 13.5 7M1 16M2 16M3 25M4 11.5M5 15 20.2M1 17M2 13M3 26M4 12.7M5 13.9 20.2M1 17M2 13M3 26M4 12.7M5 16.1 1.1M1 0.8M2 0.9M3 0.4M4 1.1M5 0.83 1.1M1 0.8M2 0.9M3 0.4M4 1.1M5 1.07 60M1 32.5M2 37M3 55M4 11M5 30.0 60M1 32.5M2 37M3 55M4 11M5 55.0 0.121 7000M1 6500M2 4700M3 370M4 120M5 5800 fQ Q Q Q Q 154.257 150M1 180M2 260M3 100M4 125M5 190 0 1 2 3 4  M1 M2 M3 M4 M5 1 M1 M2 M3 M4 M5 1Q Minimize(f M1 M2 M3 M4 M5) Таким образом, минимальная себестоимость колбасы 154.257 р.за 1 кг.без ухудшения ее качества будет достигнута при содержании говядины -12,1%, свинины- 56,45, птицы -22,95, без сухого молока, при содержании яиц - 8,6%. Сначала набраны выражение для целевой функции (себестоимости) и присвоены про- извольные начальные приближения переменным. Затем набирается ключевое слово GIVEN, открывающее блок решения систем уравнений, после чего набираются условия неотрица- тельности и ограничения переменных. . В заключение c помощью встроенной функции Q= minimize(f, M1,M2,M3,M4,M5) вычисляется минимальная себестоимость f(Q0,Q1,Q2,Q3,Q4) и значения переменных в виде вектора Q. ЛАБОРАТОРНАЯ РАБОТА №5. ВЫБОР ОПТИМАЛЬНОЙ ТРАЕКТОРИИ (Динамическое программирование). Системы, изменяющиеся во времени называются динамическими. В динамических сис- темах процесс управления разбивается на несколько последовательных шагов, причем реше- ние, принимаемое на каком либо шаге, зависит от результатов выполнения решения преды- дущего шага. Такие процессы называются многошаговымипроцессамипринятия решения. Понятие вариационной задачи. Математическая формулировка динамических задач оптимального управления сводится к следующему. Имеется объект управления, состояние которого характеризуется системой дифференциальных уравнений. x' g(x u) x(0) c(1) Характер процессов в объекте управления можно изменять, используя то или иное уп- равление u из пространства допустимых управлений U. В общем случае управление u может быть также многомерной величиной. За критерий качества управления принимается ин- тегральная оценка вида T J=Q[x(t),u(t)]dt (2), 1 1 0 имеющая физический смысл потерь, где Т – время протекания процесса управления, a Q1[x(t),u(t)]=q1(t) – мгновенные потери в момент t при состоянии системы x(t) и управлении u(t). Добавочными ограничениями могут быть ограничения, накладываемые на количество ресурсов или пределы изменения некоторых параметров, выражающиеся математически со- отношением T H[ x(t), u(t)]dt K 0 (3) Оптимальнымназываетсятакоеуправлениеизмножествадопустимыхуп-равлений U, при котором для объекта, описываемого дифференциальным уравнением (1),изаданныхограниченияхнаиспользуемыересурсы(3)критерийкачествауправления(2) принимаетминимальное(максимальное)значение. Сформулированная подобным образом задача оптимального управления относится к классу вариационных задач, решением которых занимается раздел математики, получивший название вариационного исчисления. Величина J1(u), определяемая соотношением (2), получила название функционала. В отличие от функции, например f{x), численные значения которой задаются на мно- жестве значений аргумента х, численные значения функционала J1(u) задаются на множестве всевозможных управлений u(t). Задача нахождения оптимального управления сводится к тому, чтобы из множества до- пустимых управлений U выбрать такое, при котором функционал J1(u) принимает мини- мальное численное значение. При отыскании оптимального управления вариационными методами приходится стал- киваться с трудностями, ряд которых носит принципиальный характер: Вариационные методы дают возможность находить только относительные максиму- мы и минимумы функционала J(u), тогда как интерес представляет нахождение абсолютного максимума или минимума. На значения управляющих сигналов обычно бывают наложены ограничения, делаю- щие невозможным поиск оптимального управления вариационными методами. Трудности, состоящие на пути решения задачи оптимизации управления, привели к ин- тенсивному изучению проблемы оптимальности рядом ученых в Советском Союзе и в США. Советские математики Л. С. Понтрягин и его ученики В. Г., Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко создали теорию оптимального управления, в основе которой лежит сформу- лированный Л. С. Понтрягиным принцип максимума. Этот принцип позволил поставить теорию оптимального управления на строгую математическую основу и открыл широкие возможности для ее практического применения в области автоматических систем управле- ния. Американский математик Р.Беллман разработал иной подход к вычислению оптималь- ных процессов, получивший название динамического программирования. Метод динами- ческого программирования дает в руки специалиста эффективную вычислительную проце- дуру решения задач оптимизации управления, хорошо приспособленную к использованию ЭВМ. Для дискретных систем (а на ЭВМ все системы можно рассматривать как дискретные) математическая формулировка метода динамического программирования сводится к сле- дующему. Имеется объект управления, состояние которого характеризуется многомерной дис- кретной переменной. xk=(xk(1 ),.....xk(N)),k=0,1,...n1 (4) Характер процессов в объекте управления можно изменять, используя то или иное уп- равление из пространства допустимых управлений U. В общем случае управление uU мо- жет быть также многомерной величиной. Выбор управления ukпроизводится только в дис- кретные моменты, k=0,I, ., n-1. uk=(uk(1 ),...,uk(R)) Характер движения объекта управления описывается системой разностных уравнений xk+1 =xk+g(xk,uk);k=0,1, ,n1, x0 =c(5) За критерий оптимальности принимается сумма вида n1 Jn(u)= Q(xk,uk),(6) k=0 где Q (xk, uk) – потери на шаге k, зависящие от состояния объекта xkи управления на данном шаге uk.Оптимальным называется такое управление u из множества допустимых управлений U, при котором для объекта, описываемого разностным уравнением (4), крите- рий оптимальности(6) принимает минимальное (максимальное) значение. Теперь задача за- ключается в выборе таких управлений u0,u1,. un-1, которые обеспечивают минимальное зна- чение суммы (6). Это минимальное значение критерия n-шагового процесса будет зависеть только от на- чального состояния х0 и его можно обозначать fn(x0). По определению имеем: fn(x0 )=min min ...min [Q(x0 ,u0 )+Q(x1 ,u1 )+...+Q(xn1 ,un1 )] (7) u0 u1 un1 Заметим, что первое слагаемое этого выражения Q(x0,u0) зависит только от управления u0, тогда как остальные слагаемые зависят как от u0 , так и от управлений на других шагах. Так, Q(x1,u1) зависит от u1, но оно зависит и от u0, так как x1=T(x0,U0). Аналогично обстоит дело и с остальными слагаемыми. Поэтому выражение (7) можно записать в виде u fn(x0 )=min [Q(x0 ,u0 )+fn1(x1 )](8) 0 min ...min [Q(x1 ,u1 )+...+Q(xn1 ,un1 )] Заметим далее, что выражение u1 un1 представляет собой минимальное значение критерия качества управления (n–1)- шагового процесса, имеющего начальное состояние x1. Эту величину можем обозначить че- рез fn-1(x1) Таким образом, получаем: fn1(x1 )=min [Q(x1 ,u1 )+fn2 (x2 )]. (9) u1 Эти рассуждения можно повторить, если рассмотреть (n-1)-шаговый процесс, начи- нающийся с начального состояния x1. Продолжая рассуждения, получаем аналогичное выра- жение для (n-1) шагового процесса, начинающегося с состояния хl. fnl(xl)=min [Q(xl,ul)+fn(l+1 )(xl+1 )] ul (10) Уравнение (11), называемое уравнением Беллмана, представляет собой рекур- рентное соотношение, позволяющее последовательно определять оптимальное управ- ление на каждом шаге управляемого процесса. Сама идея оптимизации управления на каждом шаге отдельно, если трудно оптимизи- ровать сразу весь процесс в целом, не является оригинальной и широко используется на практике. Однако при этом часто не принимают во внимание, что оптимизация каждого шага еще не означает оптимизацию всего процесса в целом. Особенностью метода динамического программирования является то, что оно совмещает простоту решения задачи оптимизации управления на отдельном шаге с дальновидностью, заключающейся в учете самых отдален- ных последствий этого шага. Из основного свойства оптимального управления следует, что оптимизация управле- ния для произвольной стадии многошагового процесса заключается в выборе только после- дующих управлений. Поэтому бывает удобным учитывать не те шаги, которые уже были пройдены, а те, ко- торые осталось проделать, для того, чтобы привести процесс в конечное состояние. С этой точки зрения уравнение (10) удобно записать в иной форме. В выражении (10) величина n-1 означает число шагов до тконца процесса. Обозначим эту величину через k. при этом вели- чины xiи uiбудем обозначать просто через x и u.Они будут означать состояние объекта и примененное управление за к шагов до конца процесса. Последующее состояние, т.е. то, к которому объект переходит из состояния х при применении управления u, обозначим через х`. При этом соотношение (10) примет вид k f(x)=min [Q(x,u)+f u k1 (x')] (11) Пример задачи динамического программирования. Динамическую систему необ-     ходимо перевести из точки А в точку В (см.рис.1). Движение возможно только по горизонтали ходимо перевести из точки А в точку В (см.рис.1). Движение возможно только по горизонтали | |||||||||||||||||||||||||||
