методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов

• Название: Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
• Анкор: методические указания
• Дата: 19.09.2022
• Размер: 1.02 Mb.
• Имя файла: методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1.docx
• Тип: Методические указания; #685529
• страница: 5 из 19

Форматирование результатов

Способ, которым MathCAD выводит числа, называется форматом результата. Формат результата может быть установлен для всего документа (глобальный формат) или для отдельного результата (локальный формат).

Глобальный формат устанавливается командой меню ФорматРезультат. В диалоговом окне, появляющемся после выбора этой команды, устанавливается выводимая точность числа, диапазон показателя степени (если вывод чисел нужен в форме с плавающей запятой) и точность

нуля. После внесения требуемых изменений нужно нажать кнопку ОК.

Для установки формата отдельного числа нужно: щелкнуть мышью на выражении, результат которого нужно переформатировать; вызвать команду форматирования и проделать вышеописанные действия.

Построение графиков

Для построения графика используется команда меню ВставкаГрафики. Для создания декартового графика:

1. 
   Установить визир в пустом месте рабочего документа;
   
2. 
   Выбрать команду Вставка  График  Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку панели Графики. Появится шаблон декартового графика;
   

3. 
   Введите в средней метке под осью Х первую независимую переменную, через запятую – вторую и так до 10, например: х1, х2, …;
   
4. 
   Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую – вторую и т. д., например: у1(х1), у2(х2), …, или соответствующие выражения;
   
5. 
   Щелкните за пределами области графика, чтобы начать его построение.
   

Можно построить несколько зависимостей на одном графике. Для этого нужно ввести соответствующие функции у вертикальной оси (оси ординат). Чтобы разделить описания функций, вводить их нужно через запятую.

Пример. Фрагмент рабочего документа MathCAD

Зададим функцию пользователя f

f(x)  x sin (x)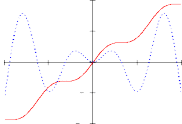
10

5

f( x) x sin( x)

10 5

0 5 10
5
10
x

ПРОГРАММИРОВАНИЕ В МАТКАДЕ.

В Маткаде имеется встроенный язык программирования. Это язык более высокого уровня, чем Бейсик и Паскаль, он позволяет производить объектно-ориентированные про- граммы.

1. При программировании в Маткаде в программе участвуют локальные переменные, действие которых распространяется только на программу, а не на весь документ в целом, частью которого является программа. Переменные, дей- ствующие во всем документе, называются глобальными.

Для составления программ необходимо, прежде всего, вызвать панель программиро- вания. Для этого следует нажать на математической панели кнопку с изображением стре- лок , прямоугольника и ромба между кнопками интегрирования и греческого алфавита.

Появится новая панель – панель программирования, состоящая из кнопок:


Кнопка ADD LINE- ДОБАВЬ СТРОКУ. При ее нажатии возникает вертикальная линия, объединяющая два оператора в блок с одним входом и одним выходом. Для объеди- нения большего числа операторов кнопку следует нажимать несколько раз.
Кнопка

- это оператор присвоения, например

A  B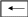

Локальной переменной А присваивается значение В.

Кнопка IF аналогична оператору условного перехода в языках Бейсик

и Паскаль, например, выражение

A  B

if C  0

означает , что , если С > 0, то A присваивается значение B.
Кнопка OTHERWISE дает возможность сделать выбор (аналог ELSE в Бейсике и Паскале).

C  D if A  B

E  F

otherwise

Если A>B, то С присваивается значение D, в противном случае E

присваивается значение F.

Кнопка FOR вводит в программу цикл с параметром (когда заранее известно, сколько циклов необходимо выполнить).Количество циклов задается несколькими способа- ми:

FOR_A 5,4,7,8

FOR_i1..10

FOR_AV

Кнопка WHILE - образует заголовок цикла с предусловием. Такой цикл использует- ся, если мы заранее не знаем, сколько циклов нам необходимо сделать для решения задачи

(Аналогичные операторы имеются в Бейсике - оператор WHILE - WEND и в Паскале -

оператор WHILE - DO).

В Маткаде набирается:

WHILE < логическое условие> < операторы, которые должны выполняться>. Ниже приводятся элементы программ в Маткаде. Их необходимо прогнать.

Пример 1. Задано значение х. В зависимости от этого значения z принимает значение 0

или 3. При изменении х меняется Z

x  1

z 

0 if

x  0

3 otherwise z  3

Пример2. Задано значение х. Значение у по-прежнему зависит от х, но вариантов здесь уже три.

x 11

y x if x² if

x 0
0 x 10

e^x otherwise
y  5.987 10⁴

Пример 3. Задано найти сумму первых десяти натуральных чисел. До начала следует присвоить сумме s нулевое значение. Так как число циклов известно, используем оператор FOR.

s s 0

for x 1 10

s s x
s  55
В процессе решения примера

1. 
   измените наибольшее значение x до 100 ,
   
2. 
   Суммируйте квадраты x
   

Пример 4. Сумма составляется в зависимости от величины x.

s s 0

for x 1 10

s s x if x 5

s s sin(x) if 5 x 8

s s cos ( x) otherwise
s  9.161

Пример 5. Применение оператора WHILE. Суммировать натуральный ряд следует до тех пор, пока сумма не превысит число 30. Здесь используются две линии ADD LINE. Преж- де всего устанавливаются начальные значения s и x. Затем пишется оператор WHILE и во втором цикле - само накапливание. Нижняя буква s показывает, по какой переменной произ- водится операция.

Порядок вычислений следующий:

1. 
   Устанавливаются начальные значения s и x.
   
2. 
   Осуществляется проверка условия. Так как оно выполняется, производится операция
   

s=s + x = 0+1.

3. 
   Проверяется условие s<30
   
4. 
   Производится вычисление s.
   

И так далее. То есть проверка производится ДО вычислений. Поэтому результат пре- вышает заданный. Проверка то проводилась ДО вычисления, тогда было s<30, а после вы- числения стало s>30 на очередной x.

Оператор WHILE проверяет условие ( s<=30) ДО ОЧЕРЕДНОГО ЦИКЛА.

s s 0

x 1

while


s 30

s s x

x x 1

s
s  36

После решения заданного примера измените предельное значение s на 15,20, 50.

Составить программы для решения следующих задач:

Задача 1. Найти сумму 25 натуральных чисел

S=1+2+3+4+. +25

Задача 2. Найти сумму 25 членов числового ряда

S=1-2+4-8+16-32+..........

ПОДСКАЗКА. Здесь каждый следующий член ряда равен предыдущему, умноженному на -2. U_n+1= U _n(-2).

Задача 3. Суммировать 25 членов ряда

S= (3+4)/2 +(6+3)/4 +(12+2)/6 + (24+1)/8 + ............

ПОДСКАЗКА. Здесь следует представить общий член ряда в виде (a+ b )/c и опреде- лить закономерности изменения каждой составляющей.

Задача 4. Как известно, индийский владетель расплатился с изобретателем шахмат следующим образом: на первую клетку шахматного поля было положено одно зерно, на вто-

рую - два, на третью - четыре (2² ), на четвертую - восемь (2³ ) и т. д. На последнюю, 64- ую клетку было положено 2⁶³ зерен. Сколько зерна получил изобретатель шахмат, если одно зерно весит 0,3 г.?

Все вышеприведенные задачи имели в ответе скаляр. Маткад позволяет получать ответ в виде вектора и матрицы. В задаче 7 ответы получаются в виде вектора.

Задача 7. Составить циклическую программу заполнения нижеприведенного v вектора числами :А) v=(1,2,3) , В) v=(3,2,1) , С) v=( 1.4.9).Ниже приведено решение варианта А.

vektor 

ORIGIN  1
_ ⁰ 

v  _ 0 _

^ ⁰ 
ORIGIN:=1 означает, что счет начинается с 1, а не с 0.

for

i  1  3

v_i  i

^{ v}1 ^
_ ¹ 



vektor  _ ^v_{2 }

vektor

 _ 2 _

^ ³ 


 _{v3 }

vektor

Здесь проведено различие между ГЛОБАЛЬНЫМИ и ЛОКАЛЬНЫМИ переменными. Программа в МАТКАДЕ является обычно частью большой задачи, переменные кото-

рой называются ГЛОБАЛЬНЫМИ.

Переменные внутри программы называются ЛОКАЛЬНЫМИ. Иногда они могут сов- падать.

В данной задаче VEKTOR - глобальная , а V, I - локальные переменные.

В программе приведена связь между ними.Определено начальное значение вектора V.

Слово VEKTOR в нижней части программы определяет, по какой переменной проис- ходит вычисление.

ЛАБОРАТОРНАЯ РАБОТА №2. РЕШЕНИЕ ЗАДАЧ МЕТОДОМ МОНТЕ- КАРЛО

Во многих задачах исходные данные носят случайный характер, поэтому для их ре- шения должен применяться статистико-вероятностный подход. На основе таких подходов построен ряд численных методов, которые учитывают случайный характер вычисляемых или измеряемых величин. К ним принадлежит и метод статистических испытаний, называемый также методом Монте-Карло, который применяется к решению некоторых задач вычисли- тельной математики, в том числе и для вычисления интегралов.-

Метод Монте-Карло состоит в том, что рассматривается некоторая случайная величина ξ , математическое ожидание которой равно искомой величине х:

Mξ=x

Проводится серия n независимых испытаний, в результате которых получается (гене- рируется) последовательность n случайных чисел ξ₁, ξ₂,….., ξ_n, и по совокупности этих зна- чений приближенно определяется искомая величина

ξ=(ξ₁ ,+ξ₂+ ξ_n)/ n x

1 ⁿ1 ⁿ nx

Mξ=M(_n ξ_i)=_nM_ ξ_i=_n=x

i=1 i=1
Интегрирование одномерных интегралов.

Интегрирование одномерных определенных интегралов методом Монте-Карло произ- водится по написанному ниже алгоритму.

b

I=_

a



f(x)dx=(b a)/ N_ f(x_i)

i=1

, (1)

где x_i - равномерно распределенная случайная величина, f(x) - подынтегральная функция, N - количество - количество случайных аргументов x_i, b и a -.верхний и нижний пределы интегрирования. В Маткаде имеется встроенная функция rnd(x), возвращающая равномерно распределенную случайную величину в диапазоне 0 - x. Для решения задач ме- тодом Монте-Карло необходимо составить программу с использованием этой функции.

Пример1. Вычислить методом Монте-Карло приведенный ниже интеграл. Приведено решение методом Монте-Карло и численным методом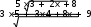
2



0

w 
y  0

N  1000000

for

i 1  N

x  rnd(2)
2



^ 5 x³  2x  8

^ dx  1.142

y  y 
3

x⁵  3x⁴  8x  9

 3



 x⁵

0

 3x⁴  8x  9

y2

w  _N

w  1.142
Пример 2. Вычислить методом Монте-Карло интеграл


_10

^{y } 

^ 3

x²  3x  8^ dx

Задача отличается от предыдущей тем, что нижний предел не равен нулю, а функция

rnd(х) вычисляет случайные числа в пределах 0-х. Поэтому здесь вычисляются два интеграла


_10



^ 3

x²  3x  8^
dx  582.833

0 10

y=_(x² +3x +8 )dx+_(x² +3x +8 )dx

3 0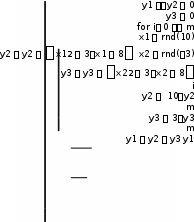
m  1000000

y  582.833

Задача 2. Вычислить методом Монте-Карло и с помощью встроенных функций Маткада нижеприведенные интегралы. Записать ошибку :

3

x³ dx

0
10

_sin(x)e^x ² x² +1dx=

3

Интегрирование многомерных интегралов.

Многомерные интегралы

b₁ b₂ b_m

  ^........ 
f(x_1, x_2,........x_m)dx₁dx₂ dx_m

a₁ a₂ a_m
вычисляются методом Монте - Карло по алгоритму

(b₁  a₁ )(b₂  a₂ )...(b_m a_m)n



_ f(x₁ ,x₂, x_m)

i=1

где х_i-случайная равномерно распределенная величина, - _{f(x1 , x2 ,...xm)}подынтегральная функция, b_i, a_i (i=1,2,…n)- верхний и нижний пределы ин- тегрирования.

Многомерные интегралы вычисляются в Маткаде методом Монте-Карло с помощью встроенной функции runif(m,a,b), возвращающей вектор из m равномерно распределенных случайных чисел в пределах от a до b.

Пример3 Вычислить методом Монте-Карло и обычным численным интеграл

2 2 2

_(x1+x2+x3)dx1dx2dx3

Данный интеграл имеет ^{0 0 0} одинаковые пределы, что

облегчает задачу.

w  y  0

for i  1 N

_2 _2 _2

v  runif(3 0 2)

y  y  v₀  v₁  v₂ i

w  22 ^2y

N

  

  

0 0 0

(x1  x2  x3) dx1dx2dx3  24

_w w  24.093
Пример 4. Вычислить методом Монте-Карло и обычным численным методом инте-

грал

5 8

y=_{∫ ∫}
x1x2dx1 dx2
_5 _8

1

w 

2

y  0

N  10000

  x1x2dx1dx2  360

 

1 2

for

i  1 N

v  runif(2 0 1) x1  4 v₀  1

x2  6 v₁  2

y  y  (x1x2) i

w  360.177

_{w } 46y

N

w

Так как интегралы имеют различные пределы, мы формируем

функцией runif вектор v с диапазоном вычислений от нуля до единицы, а затем преобразуем составляющие этого вектора, так, чтобы выдерживались заданные пределы.

Для многомерных интегралов большой размерности вычисление методом Монте-Карло происходит значительно быстрее, чем при использовании встроенной функции интегрирова- ния. Так, интеграл

2 10 8 7 9 8 5 8 9 7

^y=∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫ ∫

1 5 2 3 4 1 0 4 6 5

x1x2x3x4x5x6x7x8x9x10 dx1 dx2 dx3 dx4 dx5 dx6 dx7 dx8 dx9 dx10

вычисляется на компьютере с тактовой частотой 2 гигагерца встроенной функцией ин- тегрирования более получаса, а методом Монте-Карло- при N=100000 менее двух минут.

Задача 3. Вычислить нижеприведенные интегралы с помощью встроенных функций Маткада и методом Монте-Карло. Сравнить результаты

5 9 200 6

^y=  

0 3 100 4

5 9 3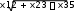

y=_ x1²(x2+x3)³ dx1dx2dx3

1 3 0

Поиск глобального экстремума функции в заданной области методом Монте –

Карло.

Нелинейные функции в большинстве случаев имеют не один, а несколько экстремумов. Самый большой максимум или минимум называется глобальным экстремумом, остальные – локальными. При решении задачи , как правило, необходимо определение глобального экс- тремума. Ниже дается решение такой задачи в Маткаде для заранее заданной области. Вне нее глобальный экстремум может быть другим.

Пусть задана многоэкстремальная функция


e
y(x)  x  ^{ 2x}  sin(15  x)
Рассмотрим ее графики при различных пределах изменения аргумента x:

Из рис.1 видно, что для области изменения аргумента -2<=x<=4 видно, что глобаль- ный экстремум находится в районе x=-2 и равен примерно 75.

x  2 1.99 4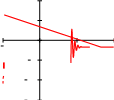
100
50

y(x) ²
0 2 4

50

100
150
x

Рис.1

Из рис.2 следует, что для другой области изменения аргумента глобальный экстремум находится районе x=0.5

x  0  0.01 

y ( x)

0.2

0.15

0.1

0.05

 0.05

 0.1

00.5

1 1.5

2 2.5 3
Рис.2

Найдем глобальный минимум этой функции в пределах изменения аргумента 0 используя метод Монте-Карло. Сформируем два вектора X и Y, присвоив их нулевым эле- ментам значение нуль.

Зададимся количеством случай- _{X0  0}

ных чисел N, которые мы будем ис-

Y₀  0

пользовать для вычисления минимума. Чем больше это количество, тем точнее будет

N 