методические указания. методичские указания МОДЕЛИРОВАНИЕ В МАТКАДЕ 1. Методические указания для проведения лабораторных работ по дисциплине Моделирование систем и процессов
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
10000С помощью функции rnd(x) создадим вектор случайных значений элементов х i . Функ- ция rnd(x) генерирует равномерно распределенные случайные числа в интервале 0-х. Из гра- фика видно, что нам достаточен интервал 0-3. i 1 N Xi rnd 3 Теперь в векторе Х помещено 100000 случайных чисел. Вычислим значения функции от них и поместим их в вектор Y. Yi yXi Величину максимального элемента этого вектора найдем, используя функцию max. Y0 maxY Y0 0.184Мы вычислили (приближенно) максимальное значение заданной функции. Теперь не- обходимо определить значение аргумента, соответствующее минимальному значению функ- ции. .Для этого составим небольшую программку и вычислим по ней ответ:  X0 X0 for i 1 N X0 Xi if X0  Y0 Yi Y0 YiX0 0 .5Задача 4. Вычислить максимумы и минимумы нижеприведенных функций: y=x4 2x3 +5 2 <x<2 y= 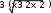 0 <x<3 0 <x<3y=sin2x− x – π/ 2 ЛАБОРАТОРНАЯ РАБОТА № 3. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВА- НИЯ Характерной тенденцией в построении современных систем управления является стремление получать системы, которые являются наилучшими. При этом задачи управления сводятся к нахождению наилучшего процесса из множе- ства возможных процессов, т.е. относятся к классу задач оптимальногоуправления. В тех случаях, когда цель управления может быть достигнута несколькими различны- ми способами, на способ управления можно наложить добавочные требования, степень вы- полнения которых может служить основанием для предпочтения одного способа управления всем другим. Во многих случаях реализация процесса управления требует затраты каких-либо ресур- сов: затрат времени, расхода материалов, топлива, электроэнергии. Следовательно, при вы- боре способа управления следует говорить не только о том, достигается ли поставленная цель, но и том, какие ресурсы придется затратить для достижения этой цели. В этом случае задача управления состоит в том, чтобы из множества решений, обеспечивающих достиже- ние цели, выбрать одно, которое требует наименьшей затраты ресурсов. В других случаях основанием для предпочтения одного способа управления другому могут служить иные требования, налагаемые на систему управления: стоимость обслужива- ния, надежность, степень близости получаемого состояния системы к требуемому, степень достоверности знаний и т. п. Математическое выражение, дающее количественную оценку степени выполне-ния наложенных на способ управления требований, называется, критерием качествауправления. Наиболее предпочтительным или оптимальным способом управления будет такой, при котором критерий качества управления достигает минимального (иногда максимального) значения. Различные виды задач управления. Различные виды задач оптимального управления отличаются друг от друга способом и последовательностью выполнения этих операций. Одношаговые задачи. В одношаговых задачах не рассматриваются методы реализа- ции принятого решения, т. е. определяются не величина и характер управляющего воздейст- вия, а непосредственно значение переменной состояния системы, которое обеспечивает наи- лучшее достижение цели управления. В одношаговых задачах критерий качества называют обычно целевой функцией или функцией выигрыша или функцией потерь. Методы ре- шения одношаговой задачи называются методами математическогопрограммирования. Математическое программирование представляет собой не аналитическую, а числен- ную форму решения, т.е. дает не формулу, выражающую конечный результат, а указывает лишь вычислительную процедуру, которая приводит к решению задачи. Поэтому методы математического программирования эффективны лишь при использо- вании ЭВМ. Задача линейного программирования является простейшим случаем задачи матема- тического программирования. Метод решения таких задач разработал советский математик Канторович, за что он получил Нобелевскую премию. Задача линейного программирования состоит в следующем: Дана система т линейно независимых уравнений с n неизвестными x1, x2 ,…….x n , назы- ваемая системой ограниченийзадачи линейного программирования: a11x1+…a1nxn=b1 ………………(1) am1x1+…amnxn=bm где, не уменьшая общности, можно считать b I>=0 , i=1…m. Характерной особенностью данной задачи является то, что число уравнений меньше числа неизвестных, т.е. m q=c1x1+….cnxn. (2) Задачи линейного программирования можно решать в различных пакетах. Для этого не нужно знать математический метод их решения, но нужно уметь поставить задачу. Задача 1. Кондитерский цех может производить три вида карамели: А, В, С. Затраты сырья, запасы сырья в цеху и прибыль от реализации каждого вида карамели приведены в таблице.
Составить план производства карамели в цеху, при котором прибыль будет максимальной. Это задача на нахождение оптимального решения. Опишем задачу математически. Обозначим через Х1 – количество производимой цехом карамели А, Х2- количество производимой цехом карамели В, Х3- количество производимой цехом карамели С, F- прибыль от производства всех трех видов карамели. Прибыль цеха от производства карамели всех трех видов будет описываться уравнени- ем F=108*Х1+112*Х2+126*Х3 И нам требуется найти максимум этой функции. Это - критерий оптимальности задачи (целевая функция). По-видимому, при производстве нельзя использовать сырья больше имеющихся в цехе запасов, т.е. 0,8*Х1+0,5*Х2+0,6*Х3<=800 0,4*X1+0,4*X2+0,3*X3<=600 0,1*X2+0,1*X3<=120 Кроме того, количество произведенных конфет не может быть отрицательным (это зна- чило бы, что цех не производит, а покупает конфеты). Поэтому, Х1>=0, X2>=0, X3>=0. Теперь мы имеем полное математическое описание задачи. Так как все уравнения и не- равенства в этой задаче линейны, мы имеем задачу ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. Решение задачи в Маткаде.  Рис.1 Решение задачи линейного программирования в Маткаде Задача 2: Для поддержания нормальной жизнедеятельности человеку необходимо по- треблять в день не менее 118 г белков, 56 г жиров, 500 г углеводов и 8 г минеральных солей. Эти питательные вещества содержатся в разных количествах в разных пищевых продуктах. В таблице приведено количество питательных веществ в различных продуктах в г/кг и цена этих продуктов за 1 кг. Необходимо составить дневной рацион, содержащий минимальную суточную норму питательных веществ при минимальной их стоимости. Пит. вещества Продукты Мясо Рыба Молоко Масло Сыр крупа Картоф
Обозначив через Х1 –количество мяса, Х2- количество рыбы, Х3- количество молока, Х4- количество масла, Х5- количество сыра, Х6- количество крупы и Х7- количество картофеля, потребляемых человеком в день, можем составить уравнение общей стоимости F пи- тания в день: F=35X1 +18X2 +5X3 +45X4 +42 X5 +12 X6 +2X7 Нам нужно найти минимум F. сюда Суммарное количество белков в рационе человека должно быть не меньше 118 г. От- 180 X1 +190 X2 +30 X3 +10 X4 +260 X5 +130 X6 +21X7 118 Такие же неравенства составляем для жиров, углеводов и солей. Имеем: 20 X1 +3X2 +40 X3 +865X4 +310X5 +30 X6 +2X7 56 50 X3 +6X4 +20 X5 +650 X6 +200 X7 500 9X1 +10 X2 +5X3 +12 X4 +60 X5 +20 X6 +10 X7 8 Кроме того, так как человек потребляет, а не выделяет продукты , ни один из аргументов Х не может быть отрицатель- ным. Отсюда: X1≥ 0 X2≥ 0 X3≥ 0 X4≥ 0 X5≥ 0 X6≥ 0 X7≥ 0 Теперь математическое описание задачи составлено полностью. Решить задачу в Маткаде по аналогией с предыдущей.. Ориентировочный ответ таков: Чтобы получить все необходимые питательные веще- ства при минимальной стоимости продуктов человек не должен есть ни мяса, ни рыбы, ни молока, ни сыра. Он должен потреблять около 20-40 г жиров в день и 500-800 г крупы или 800-900 г картофеля. При этом стоимость дневного рациона составит около 12 рублей. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
