Методические указания и контрольные задания по выполнению контрольной работы для заочного отделения по учебной дисциплине

• Название: Методические указания и контрольные задания по выполнению контрольной работы для заочного отделения по учебной дисциплине
• Дата: 01.05.2023
• Размер: 1.87 Mb.
• Имя файла: Metod_kontr_rab_po_matem_zaochn_T.doc
• Тип: Методические указания; #1100042
• страница: 4 из 7

Задание 3
1. Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.

.1. а) ; б) ;

.2. а) ; б) ;

.3. а) ; б) ;

.4. а) ; б) ; .

.5. а) ; б) ;

.6. а) ; б) ; .
.7. а) ; б) ; .

.8. а) ; б) ; .

.9. а) ; б) ;

.10. а) ; б) ;.

.11. а) ; б) ;

.12. а) ; б) ;

.13. а) ; б) ; .

.14. а) ; б) ;.

.15. а) ; б) ;.

.16. а) ; б) ;.

.17. а) ; б) ;

.18. а) ; б) ;.

.19. а) ; б) ;.

Задача Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием:

а) ; б) ;.

Решение.

► а) .

Предварительно преобразуем подынтегральную функцию, затем применив свойства неопределенного интеграла и табличный интеграл, получим: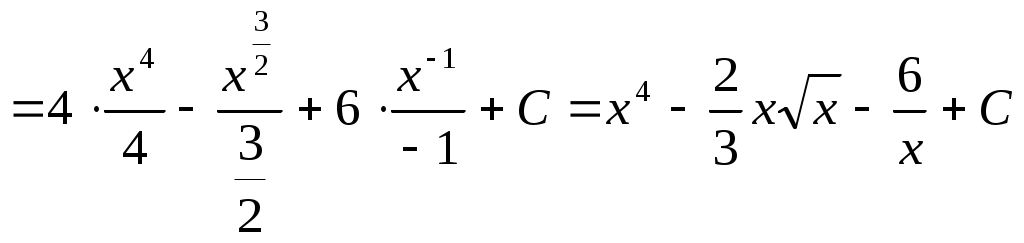

,



.

Сделаем проверку:



.

• 
  
  
• 
  
  
• 
  
  

Задание 4

Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.

.1.		2.15.	,
.2.		2.16.
.3.		2.17.
.4.		2.18	, ,
.5.		2.19.
.6.		2.20.
.7.		2.21.
.8.		2.22.
.9.	,	2.23.
.10.		2.24.
.11.		2.25.
.12.		2.26
.13.	, , ,	2.27.
.14.	,	4.28.

Типовая задача . Вычислить площадь фигуры, ограниченной параболой и прямой .

Решение.

►Площадь фигуры, ограниченная сверху непрерывной кривой , снизу – непрерывной кривой , слева – прямой и справа прямой , вычисляется по формуле

.

В тех случаях, когда заданные кривые образуют замкнутую область, и прямые 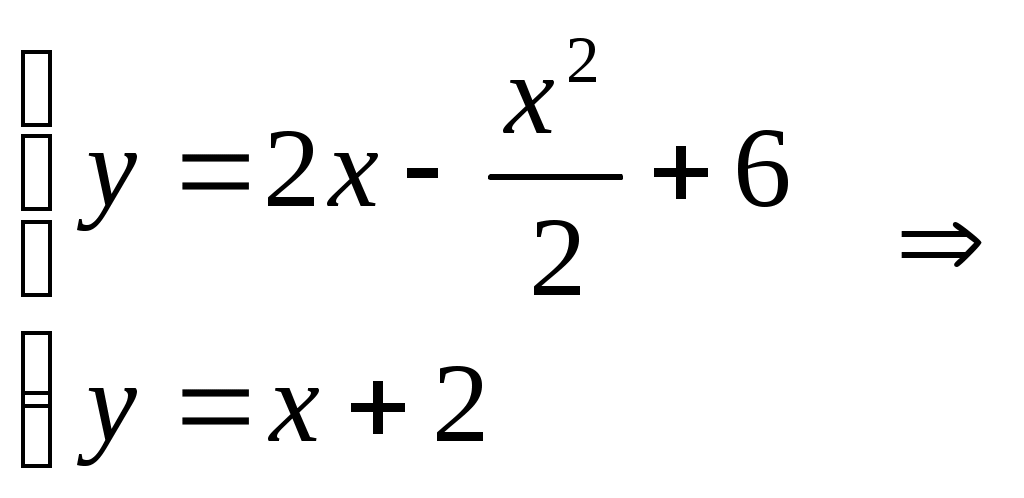и не заданы, то числа и совпадают с абсциссами точек пересечения кривых. Найдём точки пересечения заданных линий. Для этого решим совместно систему уравнений:

.

,

,

.

Получим и ; следовательно, и .

Парабола и прямая пересекаются в точках и . Для построения прямой достаточно двух найденных точек, но для параболы этих данных недостаточно. Поэтому найдем дополнительные точки:

а) вершина параболы 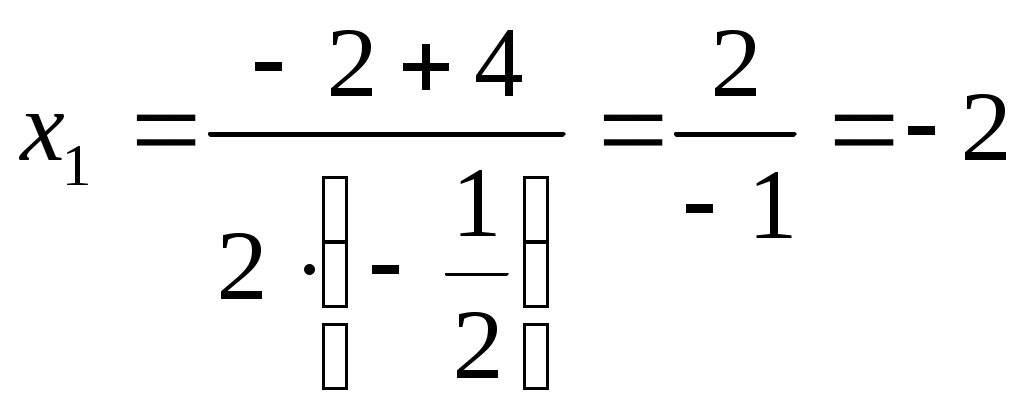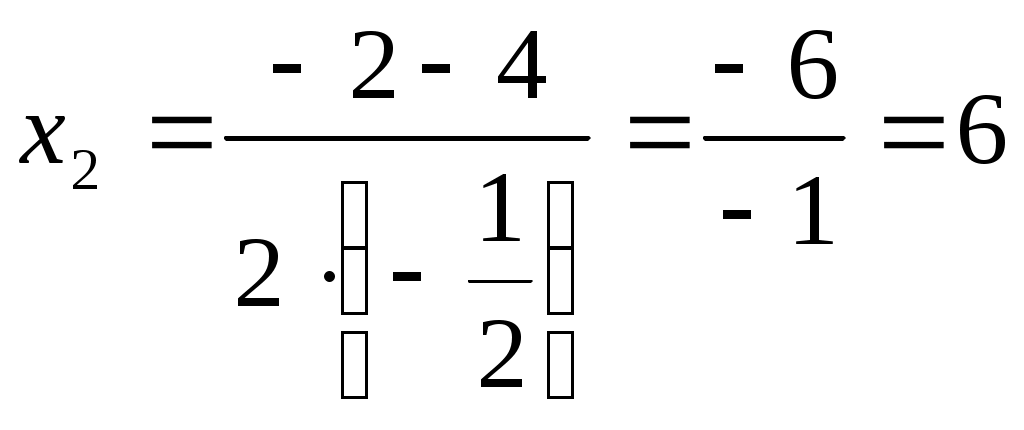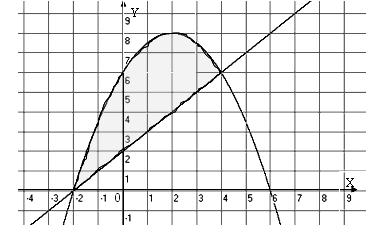расположена в точке с координатами ; в данной задаче парабола ( , ) имеет вершину в точке , т.е. .

б) Так как , следовательно, ветви параболы направлены вниз, и она пересекает ось абсцисс. Найдём точки пересечения с осью Ох:

,

,

,

.



Рис. 1

Следовательно, парабола пересекает ось Ох в точках с координатами и (рис. 1).

Применяя , получим:



.

Ответ: кв. ед.◄