Методические указания и контрольные задания по выполнению контрольной работы для заочного отделения по учебной дисциплине
 Скачать 1.87 Mb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» В Г. КАЗАНИ (ФИЛИАЛ СамГУПС В Г. КАЗАНИ) УТВЕРЖДАЮ Зам. директора по УР ______________/С.А. Семикозова / «_______»____________20__ г Методические указания и контрольные задания ПО ВЫПОЛНЕНИЮ контрольной работы для заочного отделения по учебной дисциплине ЕН.01 МАТЕМАТИКА для специальности 23.02.06 Техническая эксплуатация подвижного состава железных дорог. Базовая подготовка среднего профессионального образования Казань 2018 Контрольная работа выполняется и оформляется при соблюдении следующих правил: 1.Контрольная работа составлена при различных вариантах. 2.Контрольная работа состоит из 8 заданий. 3.Контрольная работа излагается в отдельной ученической тетради и сдается в указанные сроки.. 4.Условие задачи полностью без сокращений переписывается из заданий контрольной работы. После условия задачи отдельной строкой записывается слово «Решение»,а далее по пунктам с подробным объяснением без сокращений слов ,аккуратно и четко, со ссылкой на необходимые утверждения ,определения понятий и формулы излагается ход решения. 5.Выполненную контрольную работу необходимо предъявить преподавателю для проверки. Преподаватель проверяет правильность решения каждой задачи и в конце контрольной работы пишет рецензию на её выполнение. В рецензии отмечает ошибки решения, делает анализ их причин ,указывает на недостатки оформления, дает рекомендации по более глубокому изучению учебного материала с целью исправления допущенных ошибок, рекомендует обращение к необходимой литературе. В конце рецензии выносит заключение «зачтено» или «не зачтено». Если «не зачтено»то ,необходимо устранить замечания в той же тетради правильно и подробно изложить соответствующие преобразования в разделе «Работа над ошибками» и вновь сдать на проверку. Работа ,выполненная не по своему варианту ,не проверяется и возвращается. 6.При успешной сдачи контрольной работы имеется допуск к экзамену . Необходимо помнить ,что для приобретения и овладения избранной специальностью ,математические знания являются базовыми, требуется систематическая и упорная самостоятельная работа. Задания контрольной работы. Тема. Комплексные числа и действия над ними. . I. Теоретический материал Комплексным числом называют число вида  , где  и  ;  - мнимая единица, определяемая равенством  ; – действительная часть комплексного числа ( );  – мнимая часть комплексного числа ( ); – алгебраическая форма комплексного числа.Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу 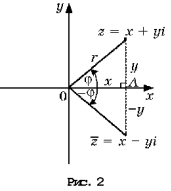ставится в соответствие точка  координатной плоскости (или радиус-вектор  ) таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки. Эта координатная плоскость называется комплексной и обозначается  .К  омплексное число  называется сопряженным для числа  (рис.1).Ч  исло  называется модулем комплексного числа  (расстояние  от начала системы координат до точки, соответствующей комплексному числу ). У Рис. 1 гол  , образованный вектором  с положительным направлением оси  , называется аргументом комплексного числа и обозначается  (рис. 2).Г Рис. 2 лавное значение аргумента  удовлетворяет следующим условиям:  или  .Основные формулы Пусть даны два комплексных числа  и  .1.      ,  .2.  .3.  .4.  .Всякое комплексное число может быть представлено в тригонометрической форме:  или в показательной форме   – формула Эйлера.Если  и  , то справедливы формулы: , , ( ), – формула Муавра, ,  ,  ,  .Задание 1 1. Даны числа  и  . а) Изобразить числа и на комплексной плоскости; б) Найти  ,  ,  ,  ;в) Найти модуль и аргумент чисел и . г) Представить числа в тригонометрической и показательной форме, найти , ,  ,.
|
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 
и 