Методические указания и контрольные задания по выполнению контрольной работы для заочного отделения по учебной дисциплине
 Скачать 1.87 Mb.
|
|
Дифференциальные уравнения Решением (частным решением) уравнения  или  на интервале (a,b) называется любая функция  , которая, будучи подставлена в это уравнение вместе со своей производной φ′(x), обращает его в тождество относительно  . Уравнение  , определяющее это решение как неявную функцию, называется интегралом (частным интегралом) дифференциального уравнения. На плоскости с фиксированной декартовой прямоугольной системой координат уравнение определяет некоторую кривую, которая называется интегральной кривой дифференциального уравнения.Функция  называется общим решением уравнения  или  , если при любом допустимом значении параметра С она является частным решением этого уравнения и, кроме того, любое его частное решение может быть представлено в виде  при некотором значении  параметра C. Уравнение  , определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.. . Дифференциальные уравнения с разделяющимися переменными Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде  . Предположим, что  . Тогда уравнение можно переписать так:  . Уравнение вида называется уравнением с разделенными переменными. Интегрируя почленно уравнение , получим общее решение уравнения  :  .При решении дифференциальных уравнений с разделяющимися переменными полезно придерживаться следующей схемы: 1) разделить переменные; 2) интегрируя уравнение с разделенными переменными, найти общее решение данного уравнения; 3) найти частное решение, удовлетворяющее начальным условиям (если они заданы). Дифференциальное уравнение второго порядка и его общее решение Уравнение, содержащее производные или дифференциалы второго порядка, называется дифференциальным уравнением второго порядка. Дифференциальное уравнение второго порядка, разрешенное относительно  , имеет вид: .Простейшим дифференциальным уравнением второго порядка является уравнение вида  .Такое уравнение решается двукратным интегрированием:  , откуда  Проинтегрировав эту функцию, получим какую-то новую функцию от  , которую обозначим через  . Таким образом,  или  Итак, получили общее решение данного дифференциального уравнения, содержащее две произвольные постоянные С1 и С2. Линейные однородные дифференциальные уравнения (ЛОДУ) 2-го порядка с постоянными коэффициентами Общий вид ЛОДУ 2-го порядка с постоянными коэффициентами  ,где  – действительные постоянные.Уравнение  , полученное заменой производных  (m=0, 1, 2) искомой функции степенями  , называется характеристическим уравнением для уравнения  .
Задание 5 . Найти общий интеграл дифференциального уравнения.
Задача1 . Решить уравнение  .Решение. ►Разделяем переменные:  . Интегрируем:  , или  - общий интеграл уравненияЗадача 2. Найти общее решение уравнения  , x≠0.Решение. ►Разделим переменные. Для этого преобразуем данное уравнение следующим образом:  (полагаем здесь y≠0).Проинтегрируем обе части последнего равенства:  .Для удобства потенцирования представим y в виде  и постоянную интегрирования  в виде  , С≠0.Имеем: .Потенцируя, получим  , С≠0.◄Задача 3. Найти общий интеграл уравнения  .Решение. ►Данное уравнение является уравнением с разделяющимися переменными. Преобразуем левую часть уравнения   Разделим переменные, поделив обе части последнего уравнения на 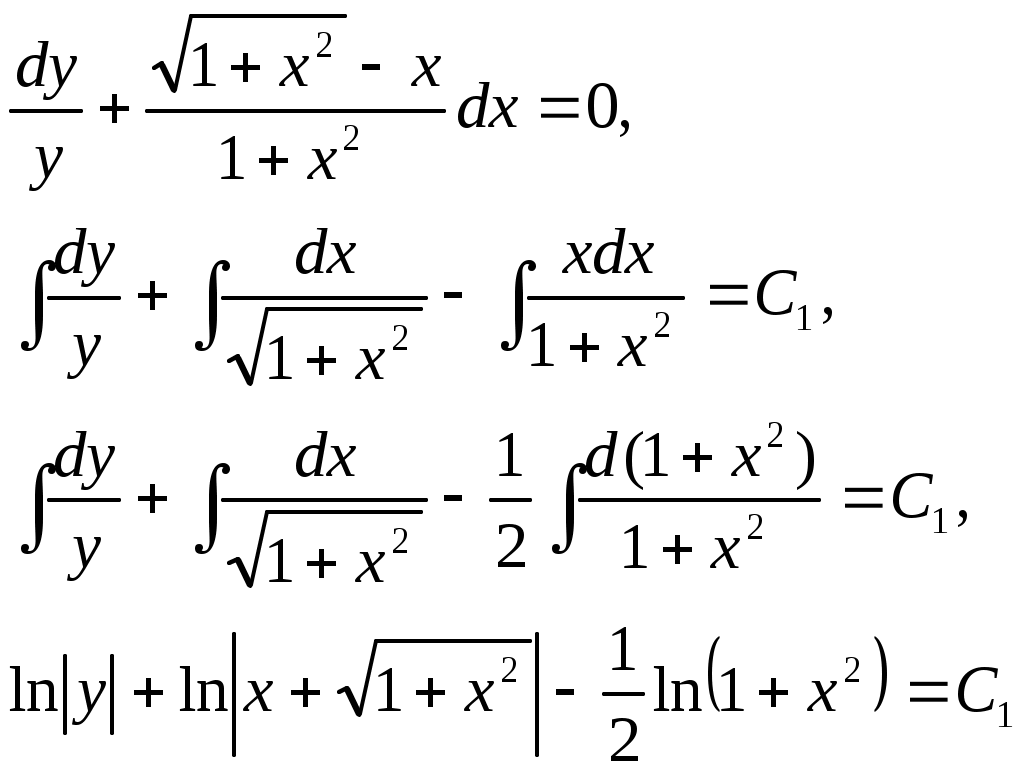 :  илиОбозначим произвольную постоянную  через  , что допустимо, так как  (при  ) может принимать любое значение от  до  .Следовательно,  или  - общий интеграл данного уравнения.◄ |
и 
- различные действительные корни;
- два совпавших корня;
два комплексно сопряжённых корня.
;
;
.
.9.
