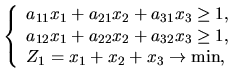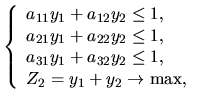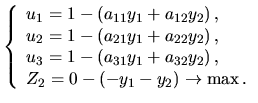методЭММ 21.06.2010. Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10

• Название: Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10
• Дата: 08.04.2022
• Размер: 0.98 Mb.
• Имя файла: методЭММ 21.06.2010.doc
• Тип: Методические указания; #454216
• страница: 7 из 7

и самостоятельной работе студентов

Магазин может завести в различных пропорциях товары трёх видов: . Их реализация и прибыль магазина зависят от вида товара и состояния спроса.

Предполагается, что спрос может иметь два состояния ( ) и не прогнозируется. Определить при данной платёжной матрице:

• 
  нижнюю цену игры;
  
• 
  верхнюю цену игры;
  
• 
  цену игры;
  
• 
  определить вероятности состояний спроса;
  
• 
  определить оптимальные пропорции в закупке товара.
  

Методические указания к выполнению

Дана платёжная матрица в виде



Нижняя и верхняя цена игры вычисляются по формулам: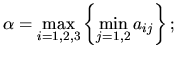





Для определения оптимальной смешанной стратегии закупки товара имеем следующую задачу линейного программирования (подробности смотрите в лекциях):

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img154.gif" \* MERGEFORMAT

(47)

где - цена игры.



Для определения вероятностей состояний спроса получаем задачу линейного программирования, двойственную к предыдущей:

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img158.gif" \* MERGEFORMAT

(48)

где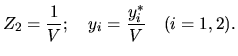



Применяем к задаче (48) симплекс-метод. Для этого приводим её к канонической форме:

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img160.gif" \* MERGEFORMAT

(49)

Системе (49) соответствует следующая таблица

	1
	1
	1
	1
	0

В этой таблице будем обозначать столбцы слева направо , строки сверху вниз . Элементы таблицы будем обозначать .

Таблицу c элементами преобразуем в таблицу с элементами . То есть, имея таблицу , получим таблицу . Делается это следующим образом.

1. 
   В строке 5 находим наименьший элемент (среди столбцов 2,3,4). Если наименьших элементов несколько, то выбираем любой из них. Пусть - этот наименьший элемент, где - номер столбца, в котором он расположен. (В таблице элементы строки 5 – это значения 0, -1 и -1. Следовательно, есть либо 3, либо 4).
   
2. 
   Выбираем все строго положительные элементы среди элементов столбца ( ) и считаем для выбранных элементов отношения . Обозначаем строку i, для которой это отношение минимально, через i₀. В результате первых двух шагов преобразования имеем разрешающий элемент .
   
3. 
   В качестве элемента - элемент ; остальные элементы первой строки и первого столбца в новой таблице остаются теми же, что и в таблице .
   
4. 
   Вычисляем остальные элементы новой таблицы:
   

1. 
   ;
   
2. 
   ;
   
3. 
   .
   

5. 
   Выполняем шаги 1-4 до тех пор, пока в строке 5 не исчезнут все отрицательные элементы (напоминаем, что в самом начале таких элементов у вас ровно 2).
   

После описанной процедуры вы имеете таблицу с элементами . Проинтерпретируем эту таблицу.

Во-первых, элемент - есть , откуда согласно (48) получаем цену игры:



Во-вторых, в столбце 1 находим элементы и смотрим соответствующие им значения в столбце 2. Эти значения и будут решением задачи (48). Остаётся только найти вероятности состояний спроса (см. (48)) по уже известной цене игры. В-третьих, обращаемся к строке 1, находим там элементы и смотрим соответствующие им значения в строке 5. Эти значения будут решением задачи (47). Заметим, что если в строке 1 нет какого-то , значение полагается равным 0. Опять-таки, остаётся вычислить оптимальную смешанную стратегию закупки товара (см.(47)).
Теоретические вопросы к самостоятельной работе студентов

1. 
   Что изучает теория игр?
   
2. 
   Понятие игры, игроков, стратегии игры, исхода игры.
   
3. 
   Платежная матрица.
   
4. 
   Определение верхней цены игры.
   
5. 
   Определение нижней цены игры.
   
6. 
   Игра с нулевой суммой.
   
7. 
   Игра в чистых стратегиях.
   
8. 
   Игра в смешанных стратегиях.
   
9. 
   Формулировка теоремы Неймана.
   
10. 
    Подход с позиции «крайнего пессимизма».
    
11. 
    Подход с позиции «крайнего оптимизма».
    
12. 
    Подход с позиции «пессимизма - оптимизма».
    

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

1. 
   Антонов А. В. Системный анализ: учебник для вузов / А. В. Антонов. – М.: Высш. шк., 2004. – 454 с.
   
2. 
   Сурмин Ю. П. Теория систем и системный анализ.: учебник для вузов – М.:МАУП, 2003. – 368 с.
   
3. 
   Бабенко Л.О. Игровые методы в управлении экономикой и бизнесом / Л. О. Бабенко, Л. Г. Лабскер – М.: Дело, 2001.
   

Дополнительная литература

4. 
   Исследование операций в экономике: учебное пособие для вузов / Кремер Н.Ш., Путко Б.А., Тришин И.М. и др. – М.: Банки и биржи, ЮНИТИ, 1997.
   
5. 
   Жилин Д. М. Теория систем: опыт построения курса. – М.: Едиториал УРСС, 2004. – 184 с.
   
6. 
   Спирин А.А. Экономико-математические методы и модели в торговле: учебное пособие для экономических и товароведных факультетов торговых вузов / А. А. Спирин, Г. П. Фомин – М.: Экономика, 1988.
   
7. 
   Черняков М. К. Модельное прогнозирование в экономике / М. К. Черняков, Н. В. Шаланов - Новосибирск: СибУПК, 1997.
   
8. 
   Шаланов Н. В. Математическая экономика. – Новосибирск; НГИ, 2006.
   
9. 
   Шаланов Н. В. Математические методы и модели в синергетике. – Новосибирск; НГТУ, 2006.
   
10. 
    Шаланов Н.В. Экономико-математические методы в торговле: учебное пособие. – Новосибирск: СибУПК, 1998.
    
11. 
    Эддоуз М. Методы принятия решений / М. Эддоуз, Р. Стенсфилд – М.: Аудит, ЮНИТИ, 1997.